Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 27
Utilize coordenadas polares para determinar o volume do sólido dado.
Dentro do cilindro quanto do elipsoide
Passo 1
Oi, galera, tudo bem?
A questão quer que a gente calcule, por meio de coordenadas polares, o volume do sólido que está dentro tanto do cilindro
Como também dentro do elipsoide
Jogando no software, teremos esse gráfico aqui:
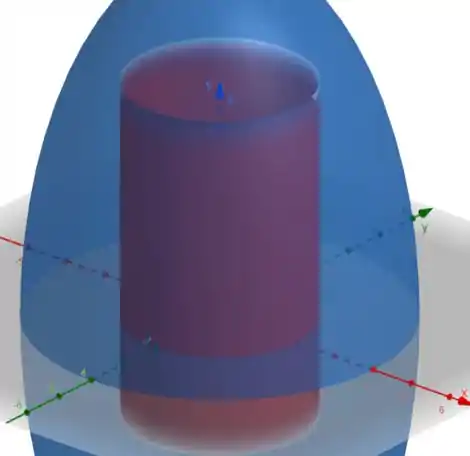
Precisamos encontrar os limites de integração e uma função para fazer a integral que encontre o volume pedido no enunciado, beleza?
Mas antes, vamos relembrar alguns termos polares:
Passo 2
Vamos começar achando os limites de integração!
Como o sólido está dentro cilindro , ele que vai limitar a região de integração.
Substituindo na equação, temos que a região de integração está limitada no seguinte intervalo
Passando para o elipsoide, vamos aplicar as coordenadas polares e isolar :
Agora podemos montar a nossa integral, não esquecendo de multiplicar pelo nosso Jacobiano
.
Então, o volume da metade superior do sólido é calculado pela integral:
Pra calcular o volume do sólido inteiro, é só multiplicar a integral por :
Passando o de dentro da integral para fora como uma constante, chegaremos a
Passo 3
Podemos separar a integral no produto de duas integrais simples, organizando os termos de acordo com seus integrandos:
Agora substituindo cada um pelos seus respectivos limites de Integración, teremos:
Show? 😉