Uma região no plano é dada. Determine equações para a transformação que mapeia uma região retangular no plano sobre , onde os lados de são paralelos aos eixos e .
é o paralelogramo com vértices .
Passo 1
Fala, galera! Tudo bem por aí?
A questão pede as equações para a transformação da região no plano para a região no plano , onde os lados da região retangular de são paralelos aos eixos e e nossa região é:
o paralelogramo com vértices
Graficamente, temos que:
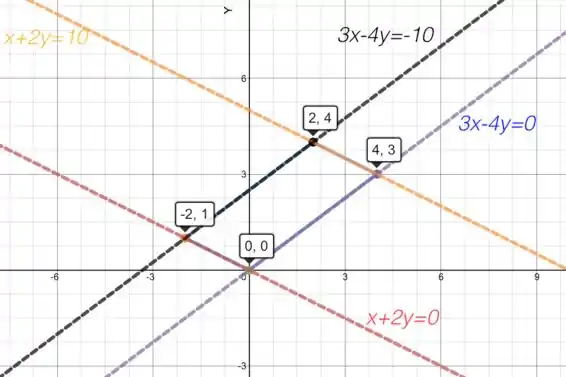
Região de integração
Nós então definimos o paralelogramo como:
E:
Se nós escolhermos e , teremos:
E:
Que é o seguinte retângulo em
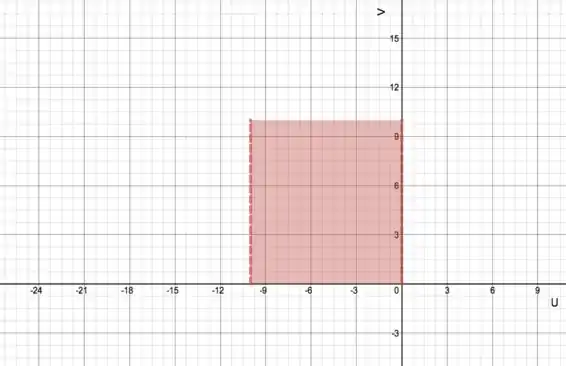
Passo 2
Seja então:
Multiplicando a por e adicionando a :
Passo 3
Multiplicando a equação por e adicionando a :