Utilize a transformação dada para calcular a integral.
, onde é o paralelogramo com vértices , , e ; ,
Passo 1
Faaaala turma, tudo bem?
Precisamos usar a seguinte transformação:
para calcular a integral abaixo:
Onde é o paralelogramo com vértices:
, , e
Como resolvemos essa questão?
Vamos lembrar juntos!! Quando temos uma integral com mudança de variáveis, podemos escrever a integral dupla da seguinte forma:
Observe que é escrito em função de e , e também aparece o Jacobiano multiplicando.
O jacobiano é esse termo:
Ele é o determinante das derivadas parciais. Onde na primeira linha temos as derivas de em relação a e , e na segunda linha as derivadas de em relação a e . Conforme pode ser visto abaixo:
Nosso objetivo, primeiro é determinar o Jacobiano. Depois vamos substituir na integral e deixar tudo em função de e .
Para encontrar os limites de integração lembre-se que temos a região do paralelogramo, que é uma figura formado por quatro retas.
Como ele forneceu os vértices, conseguimos encontrar as retas, que são do tipo:
Feito isso, substituímos e que foram dados no enunciado e vamos encontrar os intervalos de integração para e . Devemos fazer isso para cada reta do paralelogramo.
Por fim é só montar a integral e integrar!!!
Vamos nessa!!!
Passo 2
Vamos começar determinando o Jacobiano:
Antes de aplicar o determinante, vamos achar cada derivada. Vamos lembrar que as funções são:
Agora é só aplicar as derivas.
Temos que é a derivada de em função de :
E é a derivada de em função de :
Temos que é a derivada de em função de :
E por ultimo é a derivada de em função de :
Passo 3
Feito isso, substituímos no Jacobiano. Vamos ficar com:
Aqui temos um determinante de uma matriz . Que é a multiplicação da diagonal principal, menos a multiplicação da diagonal secundaria. Fazendo isso, temos:
Logo temos que o Jacobiano é:
Passo 4
A transformação mapeia o limite de para o limite da imagem .
Com o auxílio do Geogebra, obtemos a seguinte região do paralelogramo:
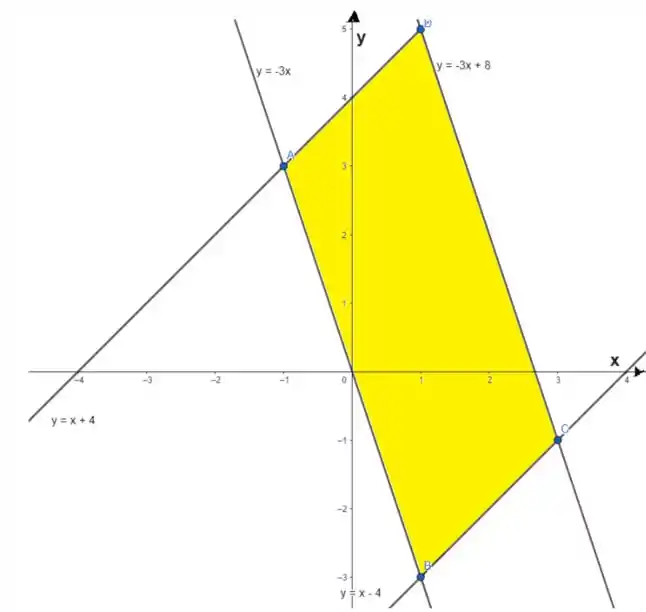
Observe que os vértices são os pontos A, B, C e D na imagem, e a região em amarelo é nossa área de interesse.
Agora vamos relacionar cada reta que une os vértices com as variáveis e . Sabemos que:
Passo 5
Vamos começar pela reta entre os vértices: e
A reta é:
Agora vamos substituir as expressões acima em função de e . Vamos ter:
Para os pontos: e
A reta é:
Substituindo as relações de e , vamos ter:
Agora os pontos: e
Temos a reta:
Substituindo as relações de e , vamos ter:
Por fim, os pontos: e
Tem a reta:
Substituindo as relações de e , vamos ter:
Observe que esse processo foi essencial para determinar os intervalos de e .
Agora temos no plano que:
Passo 6
Agora vamos substituir na integral:
Substituindo vamos ter:
Simplificando, ficamos com:
Lembre-se começamos integrando de dentro para fora. Integrando em , temos:
Aplicando os limites de integração e simplificando vamos ter:
Por fim, integramos em . Vamos ter:
Aplicando os limites de integração:
Logo, nossa resposta é: