Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.4 - Ex. 15
Verifique o Teorema de Green, usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla.
consiste no segmento de reta de a seguido pelo arco da parábola de a
Passo 1
Fala, pessoal! Tudo certinho?
Nossa questão pede para verificarmos o Teorema de Green, que traz a equação:
Onde
E a curva é o segmento de reta de a seguido pelo arco da parábola de a .
Para resolver essa questão temos que usar um sistema de computação algébrica para calcular tanto a integral de linha:
Quanto a integral dupla:
Para a integral de linha vamos ter que parametrizar nossa curva em duas curvas e e montar sua integral. Depois é só pedir para o SCA calcular o valor da integral.
Para a integral dupla, calculamos as derivadas parciais, substituímos na equação e achamos os limites de integração a região limitada pela curva . Daí montamos a integral e pegamos o resultado do SCA.
Vamos lá!
Passo 2
Vamos começar pela integral de linha, que a gente calcula:
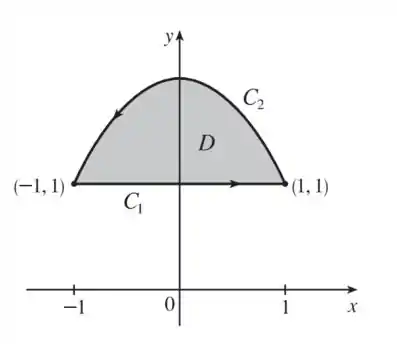
Da maneira que foi descrito temos orientado positivamente e fechada.
Para o cálculo da integral de linha vamos dividir a curva em duas partes parametrizando a reta como:
Derivando esse vetor:
Agora parametrizamos a nossa função no integrando:
Fazendo o produto escalas (soma de coordenada multiplicada por coordenada):
Usando um software, calculamos a integral:
Passo 3
E a parábola é parametrizada por:
com t variando de a
Derivando
Substituindo nossos termos na integral:
Ficamos com:
Fazendo o produto escalas (soma de coordenada multiplicada por coordenada):
Então a integral é
Passo 4
Calculando a integral dupla, tiramos nossos limites de integração da região :
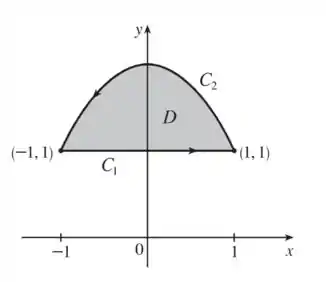
Então:
Jogando em um SCA, chegamos no resultado:
Como a integral de linha é igual a integral dupla, verificamos o Teorema de Green!