Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.8 - Ex. 14
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado e a superfície .
, é a parte do plano que está no primeiro octante, orientado para cima.
Passo 1
Oi galera, tudo bem? Vamos ver o que a questão quer!
Ela diz para a gente ver se o Teorema de Stokes é verdadeiro para o campo vetorial
Na região que é a parte do plano
Que está no primeiro octante, orientado para cima.
Primeiro octante é onde são positivos!
Vamos relembrar o Teorema de Stokes:
E vamos relembrar como se calcula o rotacional:
Portanto, vamos ter que calcular as duas integrais, tanto a de linha quanto a dupla para verificar o teorema.
A primeira coisa que vamos fazer é ver como é a região, depois vamos calcular a integral de linha. Depois disso, vamos calcular a integral dupla com o rotacional e comparar os resultados.
Bora lá?
Passo 2
Vamos fazer é ver como é essa região. Saca só esse desenho:
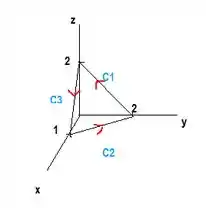
Então, para calcular a região de fronteira são três curvas e . Então:
Vamos por partes?
Passo 3
Primeiro para a curva .
No plano a equação fica . Uma parametrização possível é:
O vetor é:
E a derivada
O campo vetorial nas novas variáveis de parametrização é:
E o produto escalar entre e é:
Agora é s�� integrar! Bora lá?
Passo 4
Para a curva :
No plano a equação fica . Uma parametrização possível é:
O vetor é:
E a derivada
O campo vetorial nas novas variáveis de parametrização é:
E o produto escalar entre e é:
Agora é só integrar! Bora lá?
Passo 5
Vamos pra última curva?? 😁
Para a curva :
No plano a equação fica . Uma parametrização possível é:
O vetor é:
E a derivada
O campo vetorial nas novas variáveis de parametrização é:
E o produto escalar entre e é:
Agora é só integrar! Bora lá?
Passo 6
Ufa! Agora é só somar todos esses resultados!
Mas! Tudo isso pra dar zero no final! Kkkk Agora vamos a outra parte do teorema!
Passo 7
Para começar vamos calcular o rotacional de :
Resolvendo o determinante:
Temos então:
Passo 8
Agora vamos encontrar a função
Como a região é a parte do plano do primeiro octante, então a função é:
E o vetor normal à superfície é:
Aplicando na função temos:
E o produto escalar entre e é:
Substituindo pelo que achamos anteriormente:
Passo 9
Agora vamos ver a região de integração. Saca só no desenho:
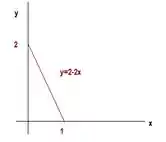
No plano , temos a reta:
E os limites de integração vão ser:
E o diferencial de área vai ser:
Passo 10
Agora é só colocar na integral!
Substituindo tudo que achamos
Fazendo a distributiva:
Resolvendo para :
Aplicando nos limites temos:
Abrindo os produtos notáveis e agrupando os termos comuns teremos:
Resolvendo para :
Aplicando os limites temos:
Simplificando:
Portanto, temos:
E
Eba! Encontramos o mesmo resultado da integral de linha! Sendo assim, verificamos o teorema 😁