Introdução aos vetores e as matrizes
Teoria
Introdução aos vetores
Falaa galerinhaaa, você já deve ter escutado muito sobre a palavra grandezas.
As grandezas estão relacionadas com aquilo que se pode ser medido, ou contado.
Por exemplo, quando você quer comprar de fita, você está utilizando uma grandeza escalar .
Esse tipo de grandeza é representado somente por um valor numérico e saber esse valor numérico já é bastante para nós.
Agora existem situações em que apenas o valor numérico não é o suficiente, como a velocidade, não basta apenas saber qual é seu valor numérico (que aqui chamaremos de módulo). Nós queremos saber também qual é a direção e o sentido na qual o carro está indo
É pra isso que existem os vetores, eles trazem mais informações para as grandezas escalares que vemos normalmente.
Representação de um vetor
O vetor é representado por meio de uma seta, que começa em um ponto e termina em outro.
Por exemplo:
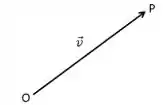
Dá uma olhada que esse vetor começa no ponto O, que é chamado de origem, e termina no ponto P que é chamado de extremidade.
A notação que temos para um vetor é uma letra minúscula com uma seta em cima, ou seja :
Também podemos escrever usando os pontos de origem e extremidade:
Quando quisermos saber o valor da coordenada que representa o vetor fazemos o ponto da extremidade menos o ponto da origem. Ou seja:
Agora observa que, usar essa seta nos mostra o que queríamos saber antes:
- Módulo (comprimento, ou tamanho).
- Direção (posição horizontal, vertical, norte, sul, leste, oeste...)
- Sentido (de O para P).
Tipos de vetores
Agora vamos ver que tipos de vetores existem:
- Vetores iguais
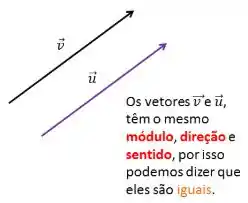
Dois ou mais vetores são iguais quando possuem o mesmo módulo, direção e sentido.
- Vetores Opostos
- Vetor unitário:
- Vetores colineares :
- Vetores coplanares:
- Matriz nula:
- Matriz coluna:
- Matriz linha:
- Matriz quadrada:
- Matriz identidade:
- Matriz transposta:
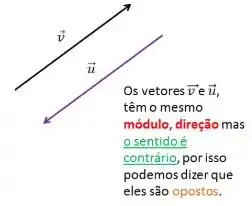
Dois ou mais vetores são opostos quando possuem o mesmo módulo e direção. Mas o sentido é contrário.
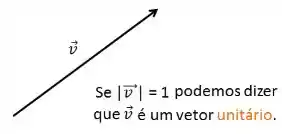
Quando o módulo do vetor é um, temos um vetor unitário.
Dizemos que dois ou mais vetores são colineares se eles possuem a mesma direção, eles podem estar paralelos ou na mesma reta ( um embaixo e outro em cima).
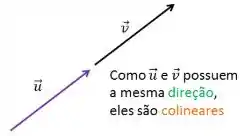
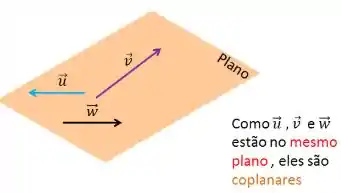
Quando dois ou mais vetores estão no mesmo plano, dizemos que eles são coplanares.
Dois vetores sempre são coplanares, porém 3 já podem não ser mais.
Introdução às matrizes
Dá uma olhadinha nisso aqui:
Você já deve ter se deparado alguma vez com algo parecido, bom isso é o que chamamos de Matriz.
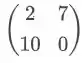
Uma matriz pode ser encarada como uma tabela, com m linhas e n colunas.
Nesse caso temos duas linhas e duas colunas, e cada um desses elementos, nós chamamos de termos da matriz.
E ela pode ser vista como uma tabela, por exemplo, a quantidade de alunos de duas turmas que participaram de uma palestra que ocorreu no período matutino e vespertino.
Representação genérica de uma matriz
Cada um dos termos da matriz vai ter uma “localização’’ própria dentro dela. Por isso é usado a notação:
é a linha onde o termo se encontra, e é a coluna.
Assim, uma matriz de forma mais geral é:
Essa matriz tem apenas três linhas e três colunas. Mas essa ideia de cada termo vale para qualquer matriz.
Aaaah, mais uma coisinha:
Uma matriz tem a seguinte notação:
Ou seja, é sempre uma letra maiúscula, com o índice , onde é a quantidade de linhas e é a quantidade de colunas. Além disso, sua leitura é feita da seguinte forma: “matriz por ”.
Em alguns exercícios eles vão nos dar o termo geral da matriz e vão pedir para montá-la.
Por exemplo:
Monte a matriz , tal que:
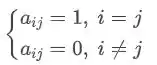
Note que a matriz vai ter 2 linhas e 2 colunas, assim a forma geral dela é;
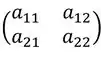
O termo geral diz que quando , o valor do termo é 1, e se , o valor do termo passa a ser 0.
Vamos fazer cada elemento, primeiro:
Temos que e , logo eles são iguais, assim nosso termo fica:
Segundo:
Temos que e , logo eles são diferentes, assim nosso termo fica:
Terceiro:
Temos que e , logo eles são diferentes, assim nosso termo fica:
Quarto:
Temos que e , logo eles são iguais, assim nosso termo fica:
Terminamos todos os termos, agora vamos montar nossa matriz:
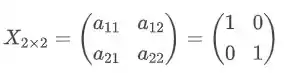
É isso, então você monta os termos a partir do termo geral que foi dado no exercício.
Tipos de matrizes
Vamos ver os tipos mais utilizados de matrizes:
Todos os elementos da matriz nula é igual a 0, independente de quantas linhas ou coluna temos. Exemplos:
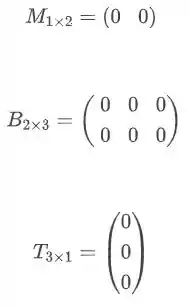
É uma matriz formada por apenas uma coluna. Exemplos:
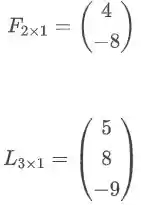
É formada por apenas uma linha. Exemplo:
Essa é uma matriz, muito importante, ela possui o número de linhas igual ao número de colunas (m=n), por exemplo:
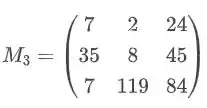
Note que usamos só um índice, para fazer o . E dizemos matriz de ordem 3, ou ordem n.
É a matriz quadrada de ordem n, que todos os elementos da diagonal principal vale 1, e o resto vale 0.
A diagonal principal começa no primeiro termo ( e segue na diagonal (. E é representada pela letra I, e o índice é a ordem da matriz.
Exemplo:
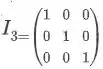
Dado uma matriz , a sua transposta é a troca de linha com colunas.
Ou seja:
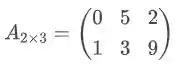
Sua transposta é :
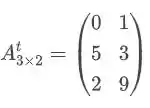
Ou seja, primeira linha vira primeira coluna, e assim vamos fazendo a troca.
É isso galeraaa, partiu exercícios.
Representação de um vetor
Tipos de vetores
Introdução às matrizes
Representação genérica de uma matriz
Tipos de matrizes
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Escreva as coordenadas da origem O e da extremidade P do seguinte vetor:
c
Passo 1
A origem de um vetor é onde têm início, e a extremidade é o final (é onde fica a pontinha da seta).
Para descobrirmos as coordenadas (x, y) de cada ponto, vamos olhar para o gráfico e ver os valores que correspondem em x e depois em y.
Passo 2
Vamos começar com a origem, podemos ver que o vetor começa quando:
Assim a coordenada da origem é:
Passo 3
Agora a extremidade, podemos ver que o valor de
E o valor de :
Assim a coordenada da extremidade é:
Resposta
Exercício Resolvido #2
Elaboração própria
Sabendo que e , cacule a coordenada do vetor :
Passo 1
Lembrando que :
Para resolver isso, nós vamos pegar a coordenada de P e subtrair a coordenada O.
Para fazer essa subtração, é só diminuir valores de x com valores de x, e de y com de y :
Essa é a cordenada do sseu vetor.
Resposta
Exercício Resolvido #3
LEZZI, Gelson et al; Matemática. São Paulo, SP: Atual, 1997. pp.362
Indique os elementos da diagonal principal e os da diagonal secundária de cada uma das seguintes matrizes quadradas:
Passo 1
Primeiro, vamos lembrar o que é diagonal principal e secundária.
Passo 2
A nossa diagonal principal nesse caso vai ser:
Então os elementos da diagonal principal são :e
Agora a secundária :
Assim, os elementos da diagonal secundária são :
e
Passo 3
Mesma ideia, nossa diagonal principal vai ser:
Assim , os elementos da diagonal principal são :
e
A secundária :
Assim, os elementos que temos na diagonal secundária são :e 0
Resposta
- Principal : e
- Principal: e
Secundária : e
Secundária: e
Exercício Resolvido #4
Elaboração própria.
Diga qual é a ordem das matrizes abaixo:
a)
b)
Passo 1
Representamos a ordem de uma matriz da seguinte maneira:
Onde:
- M é a quantidade de linhas;
- N é a quantidade de colunas.
Passo 2
a)
Nós temos apenas uma coluna e 3 linhas, ou seja, e . Dessa forma, podemos representar a ordem dessa matriz da seguinte maneira:
Passo 3
b)
Nós temos duas colunas e quatro linhas, ou seja, e . Sendo assim, podemos representar a ordem dessa matriz da seguinte maneira:
Resposta
Portanto, temos:
a)
b)
Exercício Resolvido #5
LEZZI, Gelson et al; Matemática. São Paulo, SP: Atual, 1997. pp.362
Escreva a matriz , onde
Passo 1
Para resolver esse tipo de exercício, primeiro vamos escrever a matriz genérica da ordem pedida. Nesse caso vamos ter uma matriz , 3 linhas e 3 colunas.
Uma matriz genérica de ordem 3 é :
Feito isso, agora vamos pegar cada um dos elementos e ir montando nossa matriz usando a regrinha que foi dada:
Onde i é a linha que o termo está e j é a coluna.
Passo 2
Vamos fazer cada elemento por vez, o primeiro :
Agora :
Próximo:
Assim, já montamos a primeira linha da nossa matriz :
Passo 3
Agora, vamos fazer a segunda linha
Primeiro elemento :
Segundo elemento :
Terceiro elemento:
Assim, nossa segunda linha fica :
Passo 4
Agora, vamos fazer a ultima linha :
Primeiro elemento :
Segundo elemento :
Terceiro elemento:
Assim, nossa segunda linha fica :
Resposta
Exercício Resolvido #6
LEZZI, Gelson et al; Matemática. São Paulo, SP: Atual, 1997. pp.362
Escreva a matriz , onde
Passo 1
Para começar precisamos montar a matriz genérica da ordem que queremos, nesse caso , ou seja 4 linhas e 1 coluna:
Agora, vamos usar a regrinha em cada um dos elementos para montar nossa matriz:
Passo 2
Primeiro termo :
Segundo termo:
Terceiro termo:
Quarto termo:
Assim, nossa matriz fica :
Resposta
Exercício Resolvido #7
LEZZI, Gelson et al; Matemática. São Paulo, SP: Atual, 1997. pp.362
Escreva a matriz , onde
Passo 1
Primeiro, vamos fazer a matriz genérica de ordem
Agora, vamos analisar cada elemento e usar a regrinha :
Passo 2
Vamos montar a primeira linha da nossa matriz :
Primeiro termo;
Como , assim
Segundo termo;
Como , assim
Terceiro termo;
Como , assim
Nossa primeira linha fica :
Passo 3
Próxima linha :
Primeiro termo;
Como , assim
Segundo termo;
Como , assim
Terceiro termo;
Como , assim
Nossa segunda linha fica :
Passo 4
Ultima linha :
Primeiro termo;
Como , assim
Segundo termo;
Como , assim
Terceiro termo;
Como , assim
Nossa ultima linha fica :
Resposta
Exercício Resolvido #8
Elaboração própria
Encontre a matriz transposta da matriz:
Passo 1
Vale lembrar que para obtermos a matriz transposta de uma matriz, basta pegarmos as linhas dessa matriz e transformá-las em colunas. Vamos ver um exemplo colorido:
Repara que a primeira linha de bolinhas azul da matriz, virou a primeira coluna de bolinhas azul na matriz transposta. Repara também que a ordem das bolinhas não mudou, sempre indo da mais clara para mais escura.
Sendo assim, ao repetirmos essa ação fazemos com que as outras linhas da matriz formem as colunas da matriz transposta.
Então, o mesmo se repetiu para segunda linha de bolinhas laranjas, que virou a segunda coluna de bolinhas. E a terceira linha de bolinhas verdez, virou a terceira coluna de bolinhas verdes. Sempre da mais clara para mais escura.
Passo 2
Agora vamos fazer com a matriz do nosso problema:
Vamos começar transpondo a primeira linha, para primeira coluna.
Passamos para segunda linha, que virará a segunda coluna.
Por fim, vamos transpor a última linha, completando a nossa matriz transposta.