Modificações gráficas
Teoria
Primeiramente, o que seria alterar um gráfico? Aqui, vamos falar sobre algumas das possibilidades de mudanças que podemos fazer no gráfico de uma função, como movê-lo no plano cartesiano, refletí-lo ou deixá-lo mais ou menos inclinado.
Transformações do tipo e
Essa transformação acontece no eixo horizontal porque estamos mexendo com a variável .
Logo, temos duas possibilidades: o gráfico pode se movimentar para a direita ou para esquerda. Não há outra alternativa de “caminho” no eixo .
A pergunta que fica é: se estamos saindo de para vamos pra direita ou para a esquerda? E aí o que você acha?
Vamos ver o que acontece em um exemplo!
Exemplo: vamos começar com a função .
Como temos uma função do 2º grau, podemos afirmar que seu gráfico será uma parábola. Com algumas continhas, achamos suas raízes:
Por fim, como o da função está “sozinho”, o que o acompanha vale , que sendo positivo faz a parábola ter abertura pra cima, então o gráfico fica:
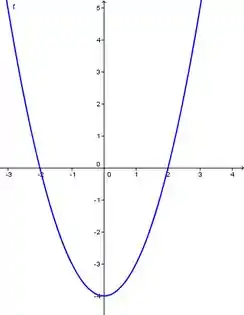
Agora vamos esboçar o gráfico da função
Aqui, vamos substituir todos os que fazem parte da nossa função por . Como só temos o , a função vai ficar
Repare que como o estava elevado ao quadrado, o que colocamos também fica elevado ao quadrado!
Mas e aí, como vamos esboçar o gráfico de ?
Primeiro, repare que:
Essa função é uma parábola igual a outra só que com raízes diferentes, que são e . Então, seu gráfico fica:
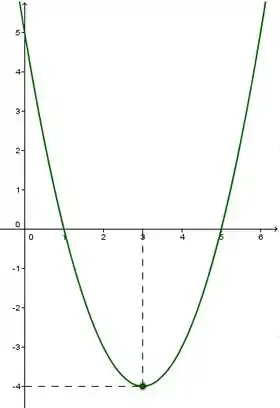
Tá beleza, mas o que um gráfico tem a ver com o outro?
Vamos colocar um do lado do outro pra conseguir enxergar o que ta rolando:
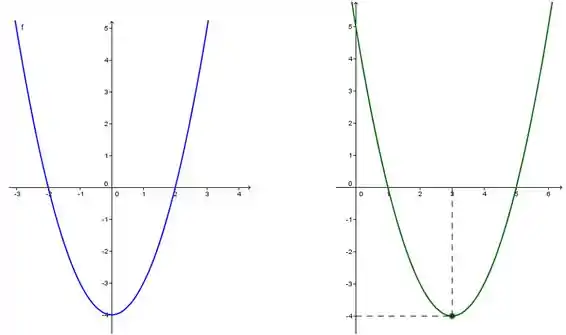
As formas dos gráficos são iguais né? Ambos são parábolas voltadas para cima.
Olhando com um pouco mais de cuidado podemos perceber que, na verdade, o gráfico verde parece ser o gráfico azul deslocado para direita. Concorda?
Mas porque fizemos isso? Repara que temos para a função azul e para a função verde.
Nessa última, tudo acontece unidades depois porque estamos tirando, subtraindo, do . Isso faz a função “atrasar” tudo em , então vai acontecer tudo igual mas com indo unidades para direita.
Opa! Aprendemos a primeira transformção, que chamamos de translação.
Conhecendo o gráfico de , o gráfico de é obtido a partir do gráfico de deslocando-o em unidades para a DIREITA!
Usando a mesma lógica, conhecendo o gráfico de , o gráfico de é obtido a partir do gráfico de , mas agora deslocando em unidades para a ESQUERDA!
Lembre que aqui estamos usando como uma constante POSITIVA!
Transformações do tipo e
Repare que estamos, novamente, somando e subtraindo uma constante , mas desta vez a constante está fora do parêntese.
Vamos ver um exemplo para entender como funciona, usando novamente a função . Então, se quisermos fazer
Temos que somar o à função que temos inicialmente:
Mais uma vez temos uma parábola e, comparando os gráficos, podemos ver como a mudança afeta a função:
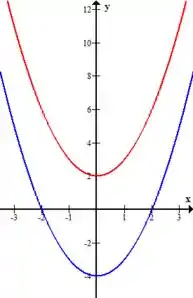
Repare que o gráfico em vermelho, que representa a função , é idêntico ao azul, que representa , mas deslocado pra cima exatamente em unidades!
Mas por que isso acontece?
Nas transformações do tipo e , a função inteira está sendo somada ou subtraída em unidades, ou seja, você está mudando o valor de e mantendo o igual. E como só estamos mudando o valor de , o gráfico se desloca também no sentido de : subindo ou descendo.
Então se conhecemos o gráfico de e queremos esboçar o gráfico de basta deslocar o gráfico de em unidades para cima!
E se quisermos esboçar o gráfico de , basta deslocar o gráfico de em unidades para baixo.
De novo, deve ser uma constante POSITIVA!
Transformações do tipo e
Mais uma vez vale lembrar que, quando estamos mexendo dentro do parêntese da expressão estamos mexendo diretamente no e se mudarmos algo fora do parêntese, estamos mexendo diretamente no !
Com isso em mente, como fazer a partir do gráfico de ?
Vamos começar com o gráfico de :
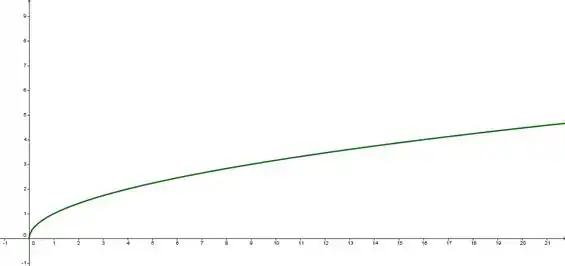
Importante lembrar que dentro de uma raiz quadrada só podem entrar números positivos, por isso o gráfico começa em e depois conforme o vai crescendo, o vai crescendo também.
Agora vamos ver o que muda para , que será:
Como fica o gráfico dessa função? Estamos perdidos? Não! Precisamos pensar quais são os números que quando eu colocar ali dentro o resultado será positivo.
Como temos o sinal de negativo na função, pro valor dentro da raiz ser positivo precisamos de números também negativos, já que Então o gráfico fica:
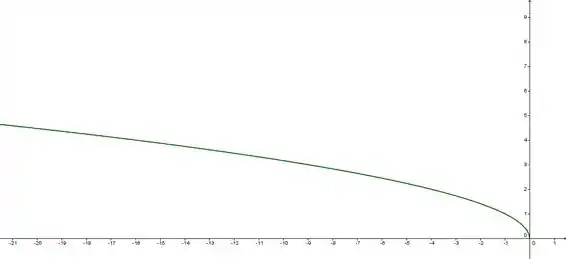
Repare que é o mesmo gráfico de antes só que “para o outro lado”.
Então, se estamos indo do gráfico de para o gráfico de , tudo que era positivo no domínio passou a ser negativo, não foi? E tudo que era negativo passou a ser positivo, já que tem um sinal de menos ali na frente. Então é como se tivéssemos invertido a orientação do eixo horizontal.
É COMO SE TIVÉSSEMOS. Não estamos mudando orientação nenhuma, isso só ajuda a entender o que tá rolando, o eixo fica lá paradinho na dele, mas é como se girássemos em torno do eixo vertical, isto é, refletimos tudo ao redor dele.
Resumindo: para esboçar o gráfico de a partir do gráfico de , basta girar o gráfico de em torno do eixo vertical!
E para obter o gráfico de , vai acontecer uma coisa beeem parecida, basta girar o gráfico de em em torno do eixo horizontal e tudo que tava em cima vai pra baixo e vice-versa, já que aqui estamos mexendo com o !
Vamos ver como exemplo o gráfico de :
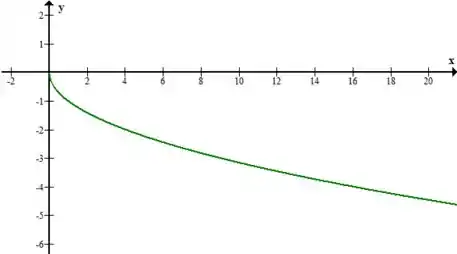
Repare que ele tem a mesma forma do gráfico de só que “de cabeça pra baixo”! E é isso que vai acontecer sempre que fizermos essas mudanças do tipo !
Isso é tudo, pessoal!
Transformações do tipo y = f ( x ) - c e y = f x + c
Transformações do tipo y = f - x e y = - f x
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Esboce o gráfico da função
Partindo do gráfico da função
Passo 1
Vamos lá!! O enunciado já nos dá a dica de que devemos começar a esboçar o gráfico da função a partir da função ! Então vamos lá!!
A função tem essa carinha aqui:
Beleza?!
Passo 2
Agora vamos fazer algo do tipo . Ou seja, onde é na função vai virar . Então a função vai ficar com essa carinha . Tá... mas o que acontece com o gráfico nesse caso?
Quando temos uma transformação do tipo essa transformação acontece no eixo horizontal, porque estamos mexendo com a variável . Então temos a possibilidade dele andar para a direita e para a esquerda.
Como estamos somando , deslocaremos unidades para a esquerda!
Perceba que na hora de fazer esse deslocamento no eixo , fazemos sempre ao contrário. Se estivermos somando , andamos unidade para trás, e se estivermos subtraindo , andamos unidade para frente. Assim, nosso gráfico se torna:
Ou seja, já temos o esboço da função !
Passo 3
Agora falta somarmos 1 para chegarmos na função .
E o que vai acontecer com o esboço do nosso gráfico quando fizermos isso?
Repare que estamos somando novamente um número, porém agora estamos somando fora dos parênteses.
Temos algo do tipo . Nesse caso, o gráfico irá se deslocar para cima ou para baixo.
Aqui como estamos somando, o gráfico irá deslocar para cima! Então, teremos
E assim conseguimos fazer o esboço da função !!! Uhulll!!
Resposta
Exercício Resolvido #2
Elaboração Própria
Faça o passo a passo de como construir o gráfico de a partir do gráfico de .
Passo 1
Opa! Bora lá!! Como o enunciado diz, precisamos partir do gráfico de :
Beleza?!
Passo 2
Primeiro vamos multiplicar o por dentro do parêntenses. O que irá acontecer com o nosso gráfico quando fizermos isso? O período da função irá mudar! O período pode ser calculado por
Sendo o que multiplica o ! Assim, como o número que está multiplicando o é o
Ou seja, estaremos encolhendo a nossa função em 2 vezes no eixo :
Passo 3
Agora falta somarmos 1 para chegarmos na função . E o que vai acontecer com o esboço do nosso gráfico quando fizermos isso?
Repare que estamos somando novamente um número, porém estamos somando fora do parêntese agora. Temos algo do tipo . Então o gráfico irá se deslocar para cima ou para baixo.
Aqui como estamos somando, o gráfico irá deslocar para cima! Então, teremos
E assim conseguimos fazer o esboço da função !!!
Resposta
Exercício Resolvido #3
Elaboração Própria
Esboce o gráfico de a partir do gráfico de .
Passo 1
Vamos lááá!!! Como o enunciado diz, precisamos partir do gráfico de
Beleza?!
Passo 2
Primeiro vamos multiplicar o por dentro do parêntenses. O que irá acontecer com o nosso gráfico quando fizermos isso? O que faremos será refletir o gráfico de em torno do eixo :
Passo 3
Agora falta multiplicarmos a função por para chegarmos na função . E o que vai acontecer com o esboço do nosso gráfico quando fizermos isso? Como estamos multiplicando a função por um número maior do que , vamos expandir o gráfico de verticalmente unidades! Ficará assim:
E assim conseguimos fazer o esboço da função !!
Resposta
Exercício Resolvido #4
Elaboração Própria
Esboce o gráfico da função a partir do gráfico de .
Passo 1
Fala Aíí!! Vamos partir do gráfico da função de
Beleza?!
Passo 2
Primeiro vamos multiplicar o por na nossa função. O que irá acontecer com o nosso gráfico quando fizermos isso? ? O período da função irá mudar! O período pode ser calculado por
Assim,
Dessa forma, estaremos esticando a nossa função ao dobro no eixo . Vamos ficar com essa carinha:
Passo 3
Agora falta somarmos 1 a nossa função para chegarmos na função . E o que vai acontecer com o esboço do nosso gráfico quando fizermos isso? Repare que estamos somando um número, porém estamos somando fora do parêntese agora. Temos algo do tipo . Então o gráfico irá se deslocar para cima:
E assim conseguimos fazer o esboço da função !!
Resposta
Exercício Resolvido #5
Elaboração Própria
Esboce os gráficos da função
Passo 1
Opa, vamos esboçar essa figurinha marota agora.
A primeira coisa que a gente faz aqui é escolher a nossa função inicial para depois fazer as devidas transformações. Saca só!
Vou escolher como função inicial um função parecida que essa que eu saiba desenha o gráfico. De cara, minha vai ser
O gráfico dessa função é o seguinte:
Passo 2
Fazendo uma transformação do tipo , teremos:
Nesta transformação, como a gente já viu, estaremos arrastando a nossa função em uma unidade para o lado esquerdo e o gráfico resultante vai ser:
Passo 3
Show de bola!
Agora, fazendo a 2ª e última transformação, que vai ser do tipo , teremos:
Que é a função que a gente quer descobrir.
Essa transformação desloca o meu gráfico em 2 unidades para baixo, certo?
Dessa forma, vamos encontrar o gráfico que é a resposta dessa questão linda, dado por:
Resposta
Exercício Resolvido #6
Elaboração Própria
Esboce o gráfico de
Passo 1
Em primeiro lugar escreveremos a regra para a função modular.
Logo:
Passo 2
Vamos construir esse gráfico em duas partes.
Primeiro, a partir de , vamos construir a reta .
Depois, antes de , vamos construir a reta .
Obs: poderíamos usar outro método para construir esse gráfico. Poderiamos desenhar o gráfico da função e usar o macete do espelho, espelhando tudo abaixo do eixo . Depois, teríamos que “subir” o gráfico em duas unidades, já que a função é .
Repare que daria no mesmo do método anterior.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração Própria
Esboce os gráficos da função
Depois, esboce os gráficos de .
Passo 1
Bem, primeiro a gente sempre começa esboçando o gráfico por uma função que a gente sabe esboçar, né? Nesse caso, sabemos esboçar a função . Seu gráfico será dado por:
Passo 2
Se a gente fizer uma pequena transformação já achamos a nossa função , sacou?
Logo, como a gente aprendeu, vamos arrastar a nossa função em unidades para baixo, tendo como resultado a figura a seguir:
Passo 3
Beleza, agora queremos achar . Lembra como faz isso?
Fazendo primeiro a transformação a gente tem que refletir a nossa figura no eixo y, beleza? Assim, vamos obter o seguinte gráfico:
Passo 4
Por fim, agora temos que achar . Quando uma transformação do tipo acontece, o que a gente faz? Boa, garoto!Fazemos uma reflexão do gráfico no eixo . Desta forma vamos ter , finalmente, o gráfico que é a resposta desta questão.
Resposta
Exercício Resolvido #8
CEFET-RJ 2017 (Adaptada)
Seja uma função real que tem o gráfico abaixo, onde . Por exemplo, no gráfico abaixo, para , assume o valor como no ponto destacado.
Sabendo disso, esboce o gráfico de e encontre os valores de para os quais a mesma assuma valor mínimo
Passo 1
A primeira coisa que vamos fazer é o módulo da função . Quando a gente faz isso, a gente transforma tudo que é negativo em positivo, ou seja, toda a parte abaixo do eixo no gráfico, a gente vai espelhar para cima. Ele vai ficar assim ó:
Show?
Passo 2
Agora, pense no seguinte: Se estamos somando a essa nossa nova função, basta que a gente suba casas com ela. Sempre que a gente fizer um somatório, a gente vai deslocar o gráfico de acordo com o somatório feito. Então ficaremos com o nosso gráfico assim:
Muito bem, percebemos que a nossa expressão gerará pontos mínimos, os pontos . Ou seja, os valores de para os quais a função assume valor mínimo são ou
Resposta
ou
Exercício Resolvido #9
Elaboração Própria
Construir os gráficos das seguintes funções definidas em :
Passo 1
- Temos que o gráfico da função cosseno é dado por
Passo 2
Agora multiplicamos por no cosseno e teremos porém,o período da função vai mudar, saca só!
O período pode ser calculado por , sendo o que multiplica o , teremos:
Desta forma, estaremos esticando a nossa função ao dobro no eixo x.
Logo o gráfico da nossa função vai ser:
Passo 3
b)
O que fazer aqui?Molezinha!
Temos uma transformação do tipo com .
Desta forma estaremos encolhendo o nosso gráfico em 3 vezes no eixo y
O domínio continua o mesmo, pois não alteramos o valor de . Mas a imagem se torna o intervalo que é a imagem da função cosseno, que é dividida por 3. Assim, o nosso gráfico será:
Passo 4
c)
Bom, como multiplicamos a função seno por temos que a imagem vai se tornar o intervalo pelo mesmo motivo da letra b). Assim a nossa função vai esticar em duas vezes o seu tamanho no eixo y.
Além disso também temos uma transformação do tipo com . Desta forma, estaremos diminuindo o período da função em vezes, passando a ser .
Com isso, estaremos encolhendo a nossa função em vezes no eixo x.
Desta forma, vamos ter o gráfico que é a nossa resposta final.
:D
Resposta
b)
c)
Exercício Resolvido #10
Elaboração própria
A função com a e b reais, representada graficamente a seguir, intersecta o eixo y no ponto de coordenadas (0, -1) e tem valor máximo . Qual é o valor da soma ?
Passo 1
Sabemos que o “a” da nossa função apenas vai transladar nosso gráfico para cima ou para baixo, enquanto o “b” vai nos mostrar o quanto se a função foi ampliada de tamanho(duplicou, triplicou, etc)
Observe que o nosso gráfico está com um período indo de -1 a 5, ou seja, está abrangendo 6 casas, enquanto o gráfico de cosx abrange apenas 2 casas. Isso significa que triplicamos o valor da nossa função.
Agora observa o que acontece quando multiplicamos a nossa função por -1
Nos invertemos o sentido da nossa função, isso acontece com a nossa função.
Sendo assim, o valor de b será -3.
No entanto, se fizermos o gráfico da função , teremos o gráfico em vermelho abaixo.
Mas queremos chegar no gráfico que está de verde e tracejado.
Ele está duas casas acima do outro, certo?
Então basta somarmos 2 a ele. Isso significa que
A nossa função então é :
Com
Show?
Passo 2
Agora ficou fácil, vamos achar o valor da expressão pedida no enunciado
Nossa resposta então será igual a 4.