Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Seno e Cosseno da Soma e Subtração de Arcos

Ver Todos os Exercícios

Teoria

Sim, sim eu sei. O nome é gigante, mas o conteúdo não é, então pode ficar tranquilo.

Nesse texto veremos como lidar com somas e subtrações dentro do seno, cosseno e tangente que ajudam a calcular valores como: sen ⁡ 75 º

Que nada mais é que: sen ⁡ 30 º + 45 º

Tá! E em que escrever 75 º como 45 º + 30 º ajuda?! Ajuda porque podemos escrever a soma ou subtração do seno através seno de seus termos.

Soma e subtração no seno

Para o nosso exemplo, podemos escrever: sen ⁡ 75 º = sen ⁡ 30 º + 45 º = sen ⁡ 30 º ⋅ cos ⁡ 45 º + sen ⁡ 45 º ⋅ cos ⁡ 30 º =

1 2 ⋅ 2 2 + 2 2 ⋅ 3 2 = 1 4 2 + 6

Veja que conseguimos transformar um seno de um ângulo não tabelado num conjunto de senos e cossenos tabelados, o que nos ajuda bastante e reforça o quanto você tem que lembrar daquela tabelinha!

De maneira geral, vamos ter que:

sen ⁡ a ± b = sen ⁡ a ⋅ cos ⁡ b ± sen ⁡ b ⋅ cos ⁡ a

Veja que, para a soma de a e b , temos a soma do produto de seno e cosseno alternando a e b .

Para a subtração de a e b , temos a subtração do produto de seno e cosseno alternando a e b .

Para o caso que a = b , temos o arco duplo:

sen ⁡ 2 a = sen ⁡ a + a = sen ⁡ a ⋅ cos ⁡ a + sen ⁡ a ⋅ cos ⁡ a

sen ⁡ 2 a = 2 sen ⁡ a ⋅ cos ⁡ a

Soma e subtração no cosseno

O cosseno segue a mesmíssima ideia do nosso amigo seno, com a diferença só na fórmula mesmo:

cos ⁡ a ± b = cos ⁡ a ⋅ cos ⁡ b ∓ sen ⁡ a ⋅ sen ⁡ b

Veja, que para a soma de a e b, temos a subtração do produto dos cossenos e senos de a e b .

Já para a subtração, temos a soma do produto dos cossenos e senos de a e b . Fique atento nessa troca de sinal!

Novamente, para o arco duplo, temos que: cos ⁡ 2 a = cos ⁡ a ⋅ cos ⁡ a - sen ⁡ a ⋅ sen ⁡ a

cos ⁡ 2 a = cos 2 ⁡ a - sen 2 ⁡ a

Soma e subtração na tangente

A tangente tem uma formulinha um pouco mais complicada de lembrar que a do seno e cosseno: t g a ± b = t g ( a ) ± t g ( b ) 1 ∓ t g a t g ( b )  

Você pode gravá-la ou lembrar que:

tg ⁡ a ± b = sen ⁡ a ± b cos ⁡ a ± b

E usar as fórmulas das seções anteriores, que você já vai ter que saber de qualquer forma. Usando qualquer uma das opções, chegamos que, para o arco duplo:

t g 2 a = 2 t g a 1 - t g ² ( a )

Soma e subtração no seno

Soma e subtração no cosseno

Soma e subtração na tangente

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

O valor de s e n o 105 ° é:

  1. 6 4
  2. 6 + 3 4
  3. 6 + 2 4
  4. 2 4
  5. 1 2

Passo 1

Fala Aííí!! Nosso objetivo aqui é calcular o s e n o 105 ° , certo? Como podemos fazer isso?! Podemos reescrever esse ângulo da seguinte forma:

s e n o 105 ° =   s e n o 60 ° + 45 °

Tá... mas em que isso nos ajuda??

Se você reparar, conseguimos quebrar em uma soma entre dois ângulos notáveis (tabelados), concorda? Agora podemos resolver utilizando o seno da soma entre dois ângulos, que tem a seguinte carinha:

s e n a ± b = s e n a ∙ cos ⁡ b ± s e n b ∙ cos ⁡ a

Beleza?!

Passo 2

Vamos então substituir os valores dos ângulos na fórmula

s e n 60 ° + 45 ° = s e n 60 ° ∙ cos ⁡ 45 ° + s e n 45 ° ∙ cos ⁡ 60 °

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

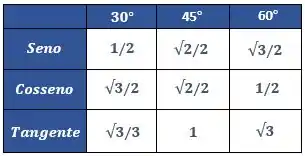
Substituindo, ficamos com

s e n 60 ° + 45 ° = 3 2 ∙ 2 2 + 2 2 ∙ 1 2

Agora é só partir pras continhas!!!

s e n 60 ° + 45 ° = 6 4 + 2 4

s e n 60 ° + 45 ° = 6 + 2 4

Show de bola?!

Resposta

L e t r a   C

Exercício Resolvido #2

Elaboração Própria

O valor de c o s 7 5 ° é:

  1. 6 + 2 4
  2. 6 + 3 4
  3. 6 - 2 4
  4. 6 - 3 4
  5. 1 2

Passo 1

Vamos láá!! Queremos calcular o c o s 75 ° , certo? Como podemos fazer isso?! Podemos reescrever esse ângulo da seguinte forma:

c o s 75 ° = c o s 3 0 ° + 45 °

Beleza, mas fizemos isso por quê??

Se você reparar, conseguimos quebrar em uma soma entre dois ângulos notáveis (tabelados), concorda? Agora podemos resolver utilizando o cosseno da soma entre dois ângulos, que tem a seguinte carinha:

c o s a ± b = c o s a ∙ cos ⁡ b ∓ s e n a ∙ s e n b  

Beleza?!

Passo 2

Vamos então substituir os valores dos ângulos na fórmula

c o s 30 ° + 45 ° = c o s 3 0 ° ∙ cos ⁡ 45 ° - s e n 30 ° ∙ s e n 45 °

Show de bola?!

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

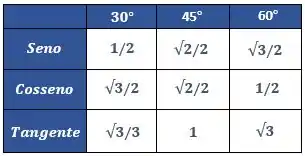
Assim, substituindo ficamos com

c o s 30 ° + 45 ° = 3 2 ∙ 2 2 - 1 2 ∙ 2 2

Agora é só partir pras continhas!!!

s e n 60 ° + 45 ° = 6 4 - 2 4

s e n 60 ° + 45 ° = 6 - 2 4

Show de bola?!

Resposta

L e t r a   C

Exercício Resolvido #3

Elaboração Própria

Qual o valor de s e n 1 5 ° ?

Passo 1

Faaaala Aíí!! Como podemos encontrar o valor de s e n 15 ° ???

Podemos reescrever esse ângulo da seguinte forma:

s e n 1 5 ° = s e n 45 ° - 30 °

Tá... Podemos... mas por que fizemos isso??

Se você reparar, conseguimos quebrar em uma soma entre dois ângulos notáveis (tabelados), concorda? Agora podemos resolver utilizando o seno da soma entre dois ângulos, que tem a seguinte carinha:

s e n a ± b = s e n a ∙ cos ⁡ b ± s e n b ∙ cos ⁡ a

Beleza?!

Passo 2

Vamos então substituir os valores dos ângulos na fórmula

s e n 45 ° - 30 ° = s e n 45 ° ∙ cos ⁡ 30 ° - s e n 30 ° ∙ cos ⁡ 45 °

Show de bola?!

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

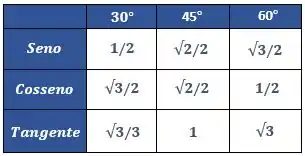
Assim, substituindo ficamos com

s e n 45 ° - 30 ° = 2 2 ∙ 3 2 - 1 2 ∙ 2 2

Agora é só partir pras continhas!!!

s e n 45 ° - 30 ° = 6 4 - 2 4

s e n 45 ° - 30 ° = 6 - 2 4

Show de bola?!

Resposta

s e n 1 5 ° = 6 - 2 4

Exercício Resolvido #4

Elaboração Própria

Calcule o valor de s e n 1 20 ° .

Passo 1

Opaaaa!! Fala Aí!! Nesse exercício queremos calcular o valor de s e n 1 20 ° , certo?! Como podemos resolver esse exercício??

Se você reparar, esse ângulo 120 ° é um ângulo que não está tabelado, certo?! O ideal aqui então para resolver esse exercício é tentar quebrar esse ângulo numa soma, subtração ou multiplicação de ângulos notáveis (tabelados). Beleza?!

Nesse caso aqui, podemos reescrever esse ângulo da seguinte forma

s e n 1 20 ° = s e n 2 ∙ 6 0 °

Note que agora temos o 2 multiplicando um ângulo que temos o valor tabelado, então vamos utilizar isso a nosso favor!! Show de bola?!

Passo 2

Para calcular o s e n 2 ∙ 60 ° precisamos utilizar a fórmula

s e n 2 a = 2 ∙ s e n a ∙ cos ⁡ a

Substituindo os valores, temos

s e n 2 ∙ 60 ° = 2 ∙ s e n 60 ° ∙ cos ⁡ 60 °

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

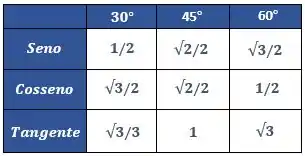
Assim, substituindo ficamos com

s e n 2 ∙ 60 ° = 2 ∙ 3 2 ∙ 1 2

Agora é só partir pras continhas!!!

s e n 2 ∙ 60 ° = 3 2

Show de bola?!

Resposta

s e n 12 0 ° = 3 2

Exercício Resolvido #5

Elaboração Própria

Calcule o valor de c o s 120 ° .

Passo 1

Vamos lááá!! Aqui queremos calcular o valor de c o s 120 ° , certo?! Como vamos fazer isso então?

Se você reparar, esse ângulo 120 ° é um ângulo que não está tabelado, certo?! O ideal aqui então para resolver esse exercício é tentar quebrar esse ângulo numa soma, subtração ou multiplicação de ângulos notáveis (tabelados). Beleza?!

Nesse caso aqui, podemos reescrever esse ângulo da seguinte forma

c o s 120 ° = c o s 2 ∙ 60 °

Note que agora temos o 2 multiplicando um ângulo que temos o valor tabelado, então vamos utilizar isso a nosso favor!! Show de bola?!

Passo 2

Para calcular o c o s 2 ∙ 60 ° precisamos utilizar a fórmula

c o s 2 a = cos 2 ⁡ a - s e n 2 a

Substituindo os valores, temos

c o s 2 ∙ 60 ° = cos 2 ⁡ 60 ° - s e n 2 60 °

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

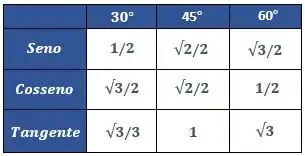
Assim, substituindo ficamos com

c o s 2 ∙ 60 ° = 1 2 2 - 3 2 2

c o s 2 ∙ 60 ° = 1 4 - 3 4

Portanto,

c o s 2 ∙ 60 ° = - 2 4 = - 1 2

Show de bola?!

Resposta

c o s 120 ° = - 1 2

Exercício Resolvido #6

Elaboração Própria

Qual o valor de t g 75 ° ?

  1. 1 + 2 3 1 - 3 3
  2. 1 + 3 3 1 - 3 3
  3. 1 + 3 3
  4. 1 + 3 2

Passo 1

Falaaa galeraaa!! Como podemos calcular a t a n g e n t e de um ângulo que não é notável, ou seja, não está tabelado?!

O ideal aqui é tentar quebrar esse ângulo numa soma, subtração ou multiplicação de ângulos notáveis (tabelados). Beleza?!

Nesse caso aqui, podemos reescrever esse ângulo da seguinte forma

t g 75 ° = t g 45 ° + 30 °

Onde os dois ângulos ( 45 ° e 30 ° ) estão na tabelinha de ângulos notáveis. Vamos então utilizar isso a nosso favor!!!

Passo 2

Para calcular o t g 45 ° + 30 ° precisamos utilizar a fórmula

t g a ± b = t g a ± t g b 1 ∓ t g a t g b

Substituindo os valores, temos

t g 45 ° + 30 ° = t g 45 ° + t g 30 ° 1 - t g 45 ° t g 30 °

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

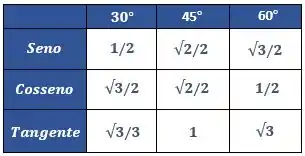
Assim, substituindo ficamos com

t g 45 ° + 30 ° = 1 + 3 3 1 - 1 ∙ 3 3

Portanto,

t g 75 ° = t g 45 ° + 30 ° = 1 + 3 3 1 - 3 3

Show de bola?!

Resposta

L e t r a   B

Exercício Resolvido #7

Elaboração Própria

Qual o valor de t g 75 ° ?

Passo 1

Falaaa galeraaa!! Como podemos calcular a t a n g e n t e de um ângulo que não é notável, ou seja, não está tabelado?!

O ideal aqui é tentar quebrar esse ângulo numa soma, subtração ou multiplicação de ângulos notáveis (tabelados). Beleza?!

Nesse caso aqui, podemos reescrever esse ângulo da seguinte forma

t g 75 ° = t g 45 ° + 30 °

Onde os dois ângulos ( 45 ° e 30 ° ) estão na tabelinha de ângulos notáveis. Vamos então utilizar isso a nosso favor!!!

Passo 2

Para calcular o t g 45 ° + 30 ° precisamos utilizar a fórmula

t g a ± b = t g a ± t g b 1 ∓ t g a t g b

Substituindo os valores, temos

t g 45 ° + 30 ° = t g 45 ° + t g 30 ° 1 - t g 45 ° t g 30 °

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

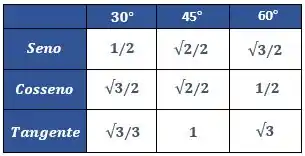
Assim, substituindo ficamos com

t g 45 ° + 30 ° = 1 + 3 3 1 - 1 ∙ 3 3

Portanto,

t g 75 ° = t g 45 ° + 30 ° = 1 + 3 3 1 - 3 3

Podemos dar aquela arrumadinha marota pra deixar a resposta de forma simplificada!! Colocando no mesmo denominador, temos

t g 45 ° + 30 ° = 1 + 3 3 1 - 3 3 = 3 + 3 3 3 - 3 3

Cortando os dois denominadores, temos

t g 45 ° + 30 ° = 3 + 3 3 - 3

Multiplicando o numerador e o denominador por 3 + 3 , temos

t g 45 ° + 30 ° = 3 + 3 3 - 3 ∙ 3 + 3 3 + 3

Fazendo a multiplicação

t g 45 ° + 30 ° = 12 + 6 3 6 = 2 + 3

Show de bola?!

Resposta

t g 7 5 ° = 2 + 3

Exercício Resolvido #8

Elaboração Própria

Considere as expressões

A = cos ⁡ x + cos ⁡ y ,             B = sen ⁡ x - sen ⁡ y

Sendo x + y = 120 o . O valor de A 2 + B 2 é:

a)2

b) cos 2 ⁡ x - cos 2 ⁡ y

c) 2 sin ⁡ x sin ⁡ y

d)4

e)1

Passo 1

Antes de substituir, vamos tentar calcular A 2 e B 2 :

A 2 = cos ⁡ x + cos ⁡ y 2 = cos 2 ⁡ x + 2 cos ⁡ x cos ⁡ y + cos 2 ⁡ y

Agora, temos que:

B 2 = sen ⁡ x - sen ⁡ y 2 = sen 2 ⁡ x - 2 sen ⁡ x sen ⁡ y + sen 2 ⁡ y

Passo 2

Substituindo:

A 2 + B 2 =

cos 2 ⁡ x + 2 cos ⁡ x cos ⁡ y + cos 2 ⁡ y + sen 2 ⁡ x - 2 sen ⁡ x sen ⁡ y + sen 2 ⁡ y

= sen 2 ⁡ x + cos 2 ⁡ x + 2 cos ⁡ x cos ⁡ y - sen ⁡ x sen ⁡ y + sen 2 ⁡ y + cos 2 ⁡ y

Pela relação fundamental da trigonometria, reduzimos a:

A 2 + B 2 = 2 + 2 cos ⁡ x cos ⁡ y - sen ⁡ x sen ⁡ y

Veja agora que esse último é cos ⁡ x + y pela soma de arcos. Então, podemos escrever: A 2 + B 2 = 2 + 2 cos ⁡ x + y

Passo 3

Como x + y = 120 º :

A 2 + B 2 = 2 + 2 cos ⁡ x + y = 2 + 2 cos ⁡ 120 º

Que, pela simetria do círculo trigonométrico, é equivalente a: cos ⁡ 120 º = - cos ⁡ 60 º = - 1 2

Logo:

A 2 + B 2 = 2 - 1 = 1

Resposta

A 2 + B 2 = 1

Letra e

Exercício Resolvido #9

Vestibular FUVEST-SP 1994

Qual o valor de:

tg ⁡ 10 o + cotg ⁡ 10 o sen ⁡ 20 o

Passo 1

Opa, para resolver isso, vamos tentar deixar tudo no mesmo grau. Vamos então tentar mudar o sen ⁡ 20 º que é mais fácil.

Pelo arco duplo: sen ⁡ 20 º = sen ⁡ 2 ⋅ 10 º = 2 sen ⁡ 10 º cos ⁡ 10 º

Substituindo:

tg ⁡ 10 o + cotg ⁡ 10 o sen ⁡ 20 o = tg ⁡ 10 o + cotg ⁡ 10 o ⋅ 2 sen ⁡ 10 º cos ⁡ 10 º

Passo 2

Agora vamos distribuir:

tg ⁡ 10 o + cotg ⁡ 10 o ⋅ 2 sen ⁡ 10 º cos ⁡ 10 º

= 2 sen ⁡ 10 º cos ⁡ 10 º tg ⁡ 10 o + 2 sen ⁡ 10 º cos ⁡ 10 º cotg ⁡ 10 o

Passo 3

Vamos agora abrir a tangente para tentar cortar: tg ⁡ 10 o = sen ⁡ 10 º cos ⁡ 10 º

cotg ⁡ 10 º = cos ⁡ 10 º sen ⁡ 10 º

Substituindo:

2 sen ⁡ 10 º cos ⁡ 10 º sen ⁡ 10 º cos ⁡ 10 º + 2 sen ⁡ 10 º cos ⁡ 10 º cos ⁡ 10 º sen ⁡ 10 º =

2 sen 2 ⁡ 10 º + 2 cos 2 ⁡ 10 º = 2 sen 2 ⁡ 10 º + cos 2 ⁡ 10 º

Que, pela relação fundamental da trigonometria:

2 sen 2 ⁡ 10 º + cos 2 ⁡ 10 º = 2 ⋅ 1 = 2

Pronto! Viu com as relações trigonométricas são poderosas? Não precisamos calcular nenhum ângulo!

Resposta

tg ⁡ 10 o + cotg ⁡ 10 o sen ⁡ 20 o = 2

Exercício Resolvido #10

Elaboração Própria

Se tan ⁡ ( a + b ) = 2 3   e tan ⁡ ( 2 a - b ) = 1 3 , calcule tan ⁡ ( 6 a ) .

Passo 1

Primeiro, vamos ver o que queremos encontrar. Pela fórmula da tangente do arco duplo:

tan ⁡ ( 6 a ) = tan ⁡ ( 3 a + 3 a ) = 2 tan ⁡ ( 3 a ) 1 - tan ⁡ ( 3 a ) 2

E agora:

tan ⁡ ( 3 a ) = tan ⁡ 2 a + a = tan ⁡ ( a ) + tan ⁡ ( 2 a ) 1 - tan ⁡ ( a ) tan ⁡ ( 2 a )

Show! Então se encontrarmos a fórmula da tan ⁡ ( 3 a ) resolvemos o problema! Tá vendo que nas tangentes que ele deu aparecem tan ⁡ ( 2 a ) e tan ⁡ ( a ) ? Será coincidência? Eu acho que não!

Passo 2

Vamos abrir as fórmulas que ele deu.

Para a primeira:

tan ⁡ ( a + b ) = 2 3

tan ⁡ ( a ) + tan ⁡ ( b ) 1 - tan ⁡ ( a ) tan ⁡ ( b ) = 2 3

Vamos multiplicar em cruz:

3 tan ⁡ ( a ) + 3 tan ⁡ ( b ) = 2 - 2 tan ⁡ ( a ) tan ⁡ ( b )

E isolar tan ⁡ ( b ) :

tan ⁡ ( b ) = 2 - 3 tan ⁡ ( a ) 3 + 2 tan ⁡ ( a )

Vamos fazer o mesmo para a segunda:

tan ⁡ ( 2 a - b ) = 1 3

tan ⁡ ( 2 a ) - tan ⁡ ( b ) 1 + tan ⁡ ( 2 a ) tan ⁡ ( b ) = 1 3

Vamos multiplicar em cruz:

3 tan ⁡ ( 2 a ) - 3 tan ⁡ ( b ) = 1 + tan ⁡ ( 2 a ) tan ⁡ ( b )

E isolar tan ⁡ ( b ) :

tan ⁡ ( b ) = 3 tan ⁡ ( 2 a ) - 1 3 + tan ⁡ ( 2 a )

Passo 3

Beleza, agora vamos igualar o que achamos pra tan ⁡ ( b ) nos dois casos:

2 - 3 tan ⁡ ( a ) 3 + 2 tan ⁡ ( a ) = 3 tan ⁡ ( 2 a ) - 1 3 + tan ⁡ ( 2 a )

E multiplicar em cruz:

6 + 2 tan ⁡ ( 2 a ) - 9 tan ⁡ ( a ) - 3 tan ⁡ ( a ) tan ⁡ ( 2 a ) = 9 tan ⁡ ( 2 a ) - 3 + 6 tan ⁡ ( 2 a ) tan ⁡ ( a ) - 2 tan ⁡ ( a )

Agora vamos agrupar os termos iguais:

9 - 9 tan ⁡ ( 2 a ) tan ⁡ ( a ) = 7 tan ⁡ ( 2 a ) + 7 tan ⁡ ( a )

Agora isolar o 7 e o 9:

9 1 - tan ⁡ ( a ) tan ⁡ ( 2 a ) = 7 tan ⁡ ( a ) + tan ⁡ ( 2 a )

9 7 = tan ⁡ ( a ) + tan ⁡ ( 2 a ) 1 - tan ⁡ ( a ) tan ⁡ ( 2 a )

Opa, opa, opa. Tá aparecendo um cara conhecido aí! Lembra da tan ⁡ ( 3 a ) ?

tan ⁡ ( 3 a ) = tan ⁡ 2 a + a = tan ⁡ ( a ) + tan ⁡ ( 2 a ) 1 - tan ⁡ ( a ) tan ⁡ ( 2 a )

É exatamente a mesma coisa! Então podemos dizer que:

tan ⁡ ( 3 a ) = 9 7

Passo 4

Agora que temos tan ⁡ ( 3 a ) , conseguimos achar tan ⁡ ( 6 a ) . Só substituir:

tan ⁡ ( 6 a ) = tan ⁡ ( 3 a + 3 a ) = 2 tan ⁡ ( 3 a ) 1 - tan ⁡ ( 3 a ) 2

tan ⁡ ( 6 a ) = 2 × 9 7 1 - 9 7 2

tan ⁡ ( 6 a ) = 18 7 1 - 81 49

tan ⁡ ( 6 a ) = 18 7 49 49 - 81 49 = 18 7 - 32 49

tan ⁡ ( 6 a ) = 18 7 × - 49 32

tan ⁡ ( 6 a ) = - 63 16

Aí você pode pensar: “Nossa, mas eu nunca iria pensar nisso na hora da prova!”. Cara, soma e subtração de arcos não tem jeito, você sempre vai ter que abrir as fórmulas pra chegar no que você quer. Da trabalho, mas pelo menos da certo. Hahaha

Resposta

tan ⁡ ( 6 a ) = - 63 16

Exercícios de Livros Relacionados

Calcule a soma dos 12 primeiros termos da série cos alpha , c o s (alpha + pi) , c o s (alpha + 2 pi) , ...
Sendo A do primeiro quadrante e arc sen x = A, ache arc cos x.
Resolva a equação:a r c t g ((1 + e^x)/(2)) + a r c t g ((1 - e^x)/(2)) = (pi)/(4)
Calcule t g (a r c s e n (3)/(4)) .
Prove as igualdades:a ) 2 a r c t g (2)/(3) + a r c cos (12)/(13) = (pi)/(2) b ) 3 a r c s e n (1)/(4) + a r c cos (11)/(16) = (pi)/(2)