Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Teste da integral

Ver Todos os Exercícios

Teoria

Introdução

Olá, pessoal! Existem vários testes que ajudam a gente a descobrir se uma série converge ou diverge. E hoje vamos aprender um teste que garante a convergência de uma série. Ele é o Teste da Integral.

Por exemplo, vamos estudar a convergência da série abaixo

∑ n = 1 ∞ n e - n 2

Repara que ela é uma mistura de série geométrica, mas tem uma cara de p-série. Então, galera, eu já adianto que aplicar outros testes para estudar essa convergência será um pouco complicado. Por isso, vamos usar aqui o teste da integral. Em resumo, ele diz o seguinte:

- Se temos uma função decrescente f ( x ) tal que f n = a n

(O que a gente ta dizendo aqui é que substituindo um valor n na função, teremos o termo geral da série ( a n ).)

- Então, se a integral dessa função converge, a série também converge.

Opa, leia a última frase de novo! Repara que o que vamos fazer aqui é integrar o termo geral da nossa série para ver a convergência dela. Vamos lá!

Função crescente e decrescente

Mas antes, repara que na definição do teste da integral, eu ressaltei que a nossa f ( x ) tem que ser decrescente. Então vamos dar uma revisada nesses conceitos?

Olha para função f ( x ) = 2 x , abaixo

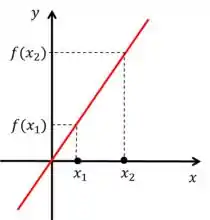
Repara que x 1 < x 2 , assim como f x 1 < f x 2 . Quando isso acontecer, nós temos uma função crescente.

Agora olha para função f x = - x + 2 ,

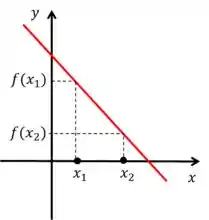
Repara que continuamos com x 1 < x 2 , mas aqui inverteu e f x 1 > f x 2 . Quando isso acontecer, nós temos uma função decrescente.

Formalmente dizemos que seja f x uma função contínua em um intervalo ( a , b ) , então temos:

f   é   c r e s c e n t e   s e   e   s o m e n t e   s e   f x 1 < f x 2   q u a n d o   x 1 < x 2   f   é   d e c r e s c e n t e   s e   e   s o m e n t e   s e   f x 1 > f x 2   q u a n d o   x 1 < x 2

Mas, galera, a gente não precisa sempre desenhar a função para saber se ela está crescendo ou não! A gente pode fazer isso derivando!

Vamos lembrar agora de um teste que nos mostra se função é crescente ou decrescente:

S e   f ' x > 0   ∀   x   e m   a , b   e n t ã o   f   é   c r e s c e n t e   e m   a , b   S e   f ' x < 0   ∀   x   e m   a , b   e n t ã o   f   é   d e c r e s c e n t e   e m   a , b S e   f ' x = 0   ∀   x   e m   a , b   e n t ã o   f   é   c o n s t a n t e   e m   a , b

Então, se você quiser descobrir aonde a função é crescente, basta derivar e ver onde que a derivada é maior que 0. Se quiser saber onde a função é decrescente, basta ver onde a derivada é menor que 0!

Com isso, vamos aplicar tudo no exemplo dado e estudar a convergência da série usando o teste da integral!

Aplicando o teste da integral

Lembra do nosso exemplo, né? Olha ele aqui de novo pronto para ser resolvido,

∑ n = 1 ∞ n e - n 2

Passo 1: Temos:

a n = n e - n 2

Se definirmos

f x = x e - x 2

Temos f n = a n . Em termos práticos, nós trocamos o n por x .Como você pode ver, a função f ( x ) é relativamente simples de se integrar, o que é um indício de que o Teste da integral deve ser uma boa.

Passo 2: Vamos ver agora se ela é decrescente! Repara que ela começa em n = 1 , então nós só temos que ver se ela decresce a partir daquele ponto. Então vamos derivar,

f x = x e - x 2

f ' x = e - x 2 1 - 2 x 2

A gente tá interessado no intervalo a partir de 1 , então vamos substituir esse ponto,

f ' 1 = e - 1 2 1 - 2 1 2 = - 1 e

Repara que para o intervalo que nós estamos interessados nossa f ’ x < 0 , então nossa função é decrescente!

Isso acima não é suficiente para dizer que a função é decrescente em todo o intervalo de 1 até –inf, apenas que ela é decrescente no ponto x=1.

Agora, partiu integrar!

Passo 3: Vamos, agora, calcular a integral do teste

∫ 1 ∞ f x   d x = ∫ 1 ∞ x e - x 2 d x

Essa é uma integral imprópria (o intervalo de integração é infinito). Você se lembra de como calcular esse tipo de integral? Basta lembrar a seguinte propriedade:

∫ a ∞ f x d x = lim b → ∞ ⁡ ∫ a b f x d x

Ou seja, substituímos o infinito por uma variável b e depois tomamos seu limite. Vamos fazer isso nesse problema:

∫ 1 ∞ x e - x 2 d x = lim b → ∞ ⁡ ∫ 1 b x e - x 2 d x

Só mudamos a forma de escrever! Agora sabemos calcular.

Sendo u = e - x 2 , temos d u = - 2 x e - x 2 d x , o que nos dá:

∫ 1 ∞ x e - x 2 d x = lim b → ∞ ⁡ ∫ - d u 2 = lim b → ∞ ⁡ - u 2

= lim b → ∞ ⁡ - e - x 2 2 1 b

= lim b → ∞ ⁡ ( e - 1 - e - b 2 ) 2

Note que

lim b → ∞ ⁡ e - b 2 = lim b → ∞ ⁡ 1 e b 2 = 0

Então

lim b → ∞ ⁡ ( e - 1 - e - b 2 ) 2 = 0 + e - 1 2 = 1 2 e

Pronto, acabamos de ver que a nossa integral converge para um ponto. Portanto pelo Teste da Integral, a série do problema também converge.

OBS: A série não precisa necessariamente começar em n = 1 . Por exemplo, se tivermos:

∑ n = 4 ∞ 1 n - 3 2

Fazemos a seguinte conta:

∫ 4 ∞ 1 x - 3 2 d x

Repara que aqui a série é decrescente apenas a partir de n = 4 . Não tem problema, a gente faz o teste da integral a partir desse valor de n , pois depois dele ela decresce! Doideira né!? Partiu exercícios!

Resumindo

De uma forma mais matemática temos

Considere a sequência a n , onde a n = f ( n ) . Sendo f uma função positiva decrescente em [ 1 ,   ∞ ) , então:

s e   ∫ 1 ∞ f x d x   c o n v e r g e ,   e n t ã o   ∑ n = 1 ∞ a n   c o n v e r g e s e   ∫ 1 ∞ f x d x   d i v e r g e ,   e n t ã o   ∑ n = 1 ∞ a n   d i v e r g e            

Mas olha só, a função TEM QUE SER DECRESCENTE! Se ela for crescente, com certeza a integral dela diverge e você não precisa fazer o teste da integral.

Certo, agora partiu exercícios!

Aplicando o teste da integral

Resumindo

Exercícios Resolvidos

Exercício Resolvido #1

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 667, exercício 4

Use o teste da integral para determinar se a série é convergente ou divergente.

∑ n = 1 ∞ 1 n 4

Passo 1

Temos

a n = 1 n 4

Logo, podemos definir

f x = 1 x 4

Assim, temos f n = a n .

Passo 2

Agora devemos verificar se a função é decrescente!

f ' x = - 1 4 x 5 4 = - 1 4 x x 4

Observe que se x > 0 ,   a raiz será positiva, então a derivada será negativa, ou seja, a função é decrescente!

Passo 3

Agora, vamos calcular a integral com intervalo finito

∫ 1 b 1 x 4 d x = ∫ 1 b x - 1 / 4   d x =

= 4 3 x 3 / 4 1 b =

= 4 ( b 3 / 4 - 1 ) 3

Passo 4

Agora vamos tomar o limite dessa expressão que encontramos.

∫ 1 ∞ 1 x 4 d x = lim b → ∞ ⁡ ∫ 1 b 1 x 4 d x = lim b → ∞ ⁡ 4 ( b 3 / 4 - 1 ) 3 = ∞

Note que lim b → ∞ ⁡ b 3 / 4 = ∞

Como a integral diverge, pelo Teste da integral, a série do problema diverge.

Resposta

A série diverge.

Exercício Resolvido #2

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 667, exercício 16

Use o teste da integral para determinar se a série é convergente ou divergente.

∑ n = 1 ∞ n 2 n 3 + 1

Passo 1

Olhando para a série, identificamos

a n = n 2 n 3 + 1

Assim, podemos definir

f x = x 2 x 3 + 1

O que nos dá f n = a n .

Passo 2

Agora precisamos determinar se essa função é decrescente! Por isso devemos calcular a derivada de f usando a regra do quociente

f ' x = 2 x x 3 + 1 - x 2 3 x 2 x 3 + 1 2 = - x 4 + 2 x x 3 + 1 2 = x - x 3 + 2 x 3 + 1 2

Como o denominador é sempre maior que zero, pois está elevado ao quadrado, devemos garantir que o numerador é negativo!

Se x > 2 3 , o numerador será negativo e a função será decrescente!

Passo 3

Vamos, agora, calcular a integral com intervalo limitado.

∫ 1 b x 2 x 3 + 1 d x

Veja, podemos definir

x 3 = u       →       3 x 2 d x = d u

Isso nos dá

= 1 3 ∫ 1 b 3 d u u + 1 =

= ln ⁡ u + 1 3 1 b 3 = ln ⁡ ( b 3 + 1 ) - ln ⁡ 2 3

Passo 4

Agora vamos tomar o limite dessa expressão que encontramos.

∫ 1 ∞ x 2 x 3 + 1 d x = lim b → ∞ ⁡ ∫ 1 b x 2 x 3 + 1 d x = lim b → ∞ ⁡ ln ⁡ ( b 3 + 1 ) - ln ⁡ 2 3 =

= lim b → ∞ ⁡ ln ⁡ ( b 3 + 1 ) 3 - ln ⁡ 2 3 = ∞

Como a integral diverge, pelo Teste da integral, a série do problema diverge.

Resposta

A série diverge.

Exercício Resolvido #3

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 667, exercício 19

Determine se a série é convergente ou divergente.

∑ n = 1 ∞ ln ⁡ n n 3

Passo 1

Temos:

a n = ln ⁡ n n 3

Logo, podemos definir

f x = ln ⁡ x x 3

Assim, temos f n = a n .

Passo 2

Vamos calcular a derivada para garantir que essa função é decrescente

f ' x = x 2 - 3 x 2 ln ⁡ x x 6 = 1 - 3 ln ⁡ x x 4

Como o denominador está elevado a potência par, ele é sempre positivo. Basta, então, analisar o numerador.

Se x > e 1 3 , a função será decrescente, pois o numerador será menor que zero.

Passo 3

Agora, vamos calcular a integral com intervalo finito.

∫ e 1 3 b ln ⁡ x x 3 d x =

Como não conseguimos identificar uma substituição direta, vamos usar a integração por partes:

∫ u d v = u v - ∫ v d u

Definindo

d x x 3 = d v   →   - 1 2 x 2 = v

ln ⁡ x = u → 1 x d x = d u

∫ ln ⁡ x x 3 d x = - ln ⁡ x 2 x 2 - ∫ - 1 2 x 2 ⋅ 1 x d x =

= - ln ⁡ x 2 x 2 + ∫ 1 2 x 3   d x =

= - ln ⁡ x 2 x 2 - 1 4 x 2 = - 2 ln ⁡ ( x ) + 1 4 x 2

∫ e 1 / 3 b ln ⁡ x x 3 d x = - 2 ln ⁡ ( x ) + 1 4 x 2 e 1 / 3 b = - 2 ln ⁡ ( b ) + 1 4 b 2 + 2 ln ⁡ e 1 / 3 + 1 4 e 1 / 3 2 =

= - 2 ln ⁡ ( b ) + 1 4 b 2 + 5 12 e 2 3

Passo 4

Agora vamos tomar o limite dessa expressão que encontramos.

∫ e 1 3 ∞ ln ⁡ x x 3 d x = lim b → ∞ ⁡ ∫ e 1 3 b ln ⁡ x x 3 d x

= lim b → ∞ ⁡ - 2 ln ⁡ ( b ) + 1 4 b 2 + 5 12 e 2 3 = lim b → ∞ ⁡ - 2 ln ⁡ ( b ) + 1 4 b 2 + 5 12 e 2 3

Como tanto o numerador quanto o denominador da razão tendem a infinito, podemos aplicar a regra de L’Hospital aqui, derivando ambos os termos:

= lim b → ∞ ⁡ - 2 b 8 b + 5 12 e 2 3 =

= lim b → ∞ ⁡ - 1 4 b 2 + 5 12 e 2 3 = 5 12 e 2 3

Note que lim b → ∞ ⁡ 1 / 4 b 2 = 0 .

Como a integral converge, pelo Teste da integral, a série do problema converge.

Resposta

A série converge.

Exercício Resolvido #4

USP - Cálculo 4 - P1 2012 – 2a

Determine se a série converge ou diverge

∑ n = 1 ∞ 1 n 1 + ln ⁡ n 2

Passo 1

Se olharmos bem esse termo da série vai para 0 quando n → ∞ , então o teste da divergência não vai ajudar.

Repara que temos ln ⁡ n e 1 n no termo geral, isso nos dá uma dica de usarmos o teste da integral.

Para o teste da integral temos que fazer

f x = 1 x 1 + ln ⁡ x 2

Antes de mais nada devemos olhar essa função e ver se ela é decrescente, para isso vamos analisar o sinal da sua derivada

f ' x = 0 - 1 + ln ⁡ x 2 + x 2 ln ⁡ x 1 x x 1 + ln ⁡ x 2 2 = - 1 + ln ⁡ x 2 + 2 ln ⁡ x x 1 + ln ⁡ x 2 2

Vamos dar uma arrumada nisso, repara que temos

1 + ln ⁡ x 2 + 2 ln ⁡ x = ln ⁡ x 2 + 2 ln ⁡ x + 1 = ln ⁡ x + 1 2

Então

f ' x = - ln ⁡ x + 1 2 x 1 + ln ⁡ x 2 2

O denominador e o numerador são sempre positivos, então com aquele menos de fora a derivada vai ser negativa sempre, assim a nossa função é decrescente e podemos usar o teste da integral.

Agora devemos olhar a convergência da integral

∫ 1 ∞ f x d x = ∫ 1 ∞ 1 x 1 + ln ⁡ x 2 d x

Se essa integral convergir então a série converge, se ela divergir a série diverge.

Passo 2

Vamos para essa integral

∫ 1 ∞ 1 x 1 + ln ⁡ x 2 d x

Essa integral com ∞ é uma integral imprópria, e ela não tem nenhum ponto de descontinuidade nesse intervalo, então vamos ter

∫ 1 ∞ 1 x 1 + ln ⁡ x 2 d x = lim a → ∞ ⁡ ∫ 1 a 1 x 1 + ln ⁡ x 2 d x

Temos que resolver

∫ 1 x 1 + ln ⁡ x 2 d x

Vamos fazer

ln ⁡ x = u

d u = 1 x d x

E a integral vai ficar

∫ 1 x 1 + ln ⁡ x 2 d x = ∫ 1 1 + u 2 d u

Passo 3

Vamos resolver essa integral

∫ 1 1 + u 2 d u

Aqui vamos usar substituição trigonométrica, como temos u 2 + 1 vamos fazer

u = 1 ⋅ tan ⁡ θ

Assim

d u = sec 2 ⁡ θ d θ

Substituindo na integral

∫ 1 1 + u 2 d u = ∫ 1 tan ⁡ θ 2 + 1 sec 2 ⁡ θ d θ = ∫ sec 2 ⁡ θ d θ tan 2 ⁡ θ + 1

Lembrando que

sec 2 ⁡ θ = tan 2 ⁡ θ + 1

Assim vamos ter

∫ sec 2 ⁡ θ d θ tan 2 ⁡ θ + 1 = ∫ sec 2 ⁡ θ d θ sec 2 ⁡ θ = θ

Como

θ = arctan ⁡ u

Vamos ter

∫ 1 1 + u 2 d u = arctan ⁡ u

Passo 4

Isso nos diz que

∫ 1 1 + u 2 d u = arctan ⁡ u

Voltando para x

∫ 1 x ( 1 + ln ⁡ x 2 d x = arctan ⁡ ln ⁡ x

Passo 5

Voltando para o nosso limite temos

lim a → ∞ ⁡ ∫ 1 a 1 x ( 1 + ln ⁡ x 2 d x = lim a → ∞ ⁡ arctan ⁡ ln ⁡ x 1 a = lim a → ∞ ⁡ arctan ⁡ ln ⁡ a - arctan ⁡ ln ⁡ 1

Temos

lim a → ∞ ⁡ arctan ⁡ ln ⁡ a - arctan ⁡ 0 = lim a → ∞ ⁡ arctan ⁡ ln ⁡ a + 0 = π 2

E essa integral converge a série converge

Resposta

Converge

Exercícios de Livros Relacionados

9-26. Determine se a série é convergente ou divergente.20. ∑ n = 1 ∞ 1 n 2 + 6 n + 13
Leonhard Euler foi capaz de calcular a soma exata da série p com p = 2 : ζ x = ∑ n = 1 ∞ 1 n 2 = π 2 6 Utilize esse fato para encontrar a soma de cada série. ∑ n = 1 ∞ 1 ( 2 n ) 2
Leonhard Euler foi capaz de calcular a soma exata da série p com p = 2 : �� x = ∑ n = 1 ∞ 1 n 2 = π 2 6 �� Utilize esse fato para encontrar a soma de cada série.b) ∑ n = 3 ∞ 1 ( n + 1 ) ² ²
9-26. Determine se a série é convergente ou divergente.18. ∑ n = 3 ∞ 3 n - 4 n 2 - 2 n
Quantos termos da série ∑ n = 2 ∞ 1 / n ln ⁡ n 2 você precisaria somar para encontrar sua soma com precisão de 0,01?