Teste da Série Alternada
Produzido por Carolina SabaTeoria
Fala galera. Sejam bem vindos ao Responde Aí, a plataforma de exatas criada para ajudar você a mandar super bem nas suas provas da faculdade!
Estamos aqui hoje para te ajudar a entender um conteúdo importante no estudo de séries. o teste da série alternada.
Preparado para aprender de uma vez por toda? Então só bora!
Conhecimentos Prévios
O que é série alternada?
O que vamos estudar agora são as séries que mudam de sinais a cada termo. Como assim? Veja só:
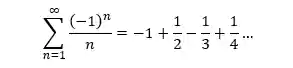
Percebeu que os sinais se alternam? Isso que nós chamamos de Série alternada.
Quando você vir, então, um termo
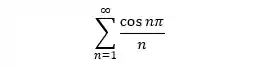
De cara, você não vê que essa é uma série alternada, mas veja seus termos:
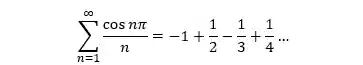
Essa é exatamente a mesma série que acabamos de ver, apenas escrita de forma diferente! Perceba que, como
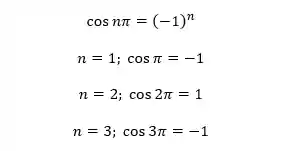
E assim por diante.
Então, a partir de agora, quando você vir um seno ou cosseno em uma série, já fique ligado, pode ser uma série alternada.
Teste da Série Alternada
Para testarmos a convergência de uma série alternada vamos usar um método específico para essas séries chamado teste da série alternada ou critério de Leibniz.
O teste da série alternada diz o seguinte:

Vamos pegar um exemplo, ok?
Olha essa série alternada aqui:
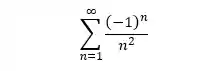
Para esse caso, a gente tem que o termo geral
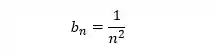
Note que
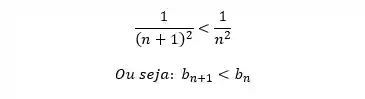
Assim, o primeiro critério do teste da série alternada é satisfeito.
Além disso, o limite do termo geral, quando
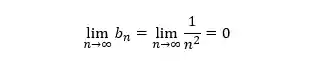
Desse modo, o segundo critério também é satisfeito e chegamos a conclusão que a série converge!
Viu? Esse teste é bem simples 😉
Convergência absoluta
Dizemos que uma série alternada é absolutamente convergente quando a série que tem termo geral igual ao módulo do termo geral da série alternada converge.
Em outras palavras:
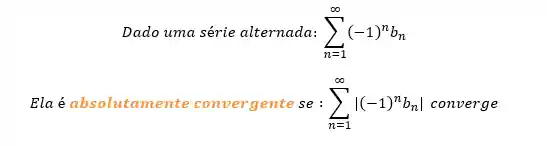
Para encontrar a convergência da série somente com termos positivos o que você vai fazer é usar os outros testes de convergência como: teste da divergência, teste da comparação, teste da comparação no limite, teste da integral, etc.
O que é interessante em achar a convergência absoluta é que toda série absolutamente convergente é convergente.
Mas, fica atento, pois nem toda série convergente é absolutamente convergente.
Convergência condicional
Uma série alternada é dita condicionalmente convergente quando ela converge como série alternada, mas não converge como série de termos positivos.
Olha essa série aqui:
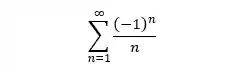
Ela é chamada de série harmônica alternada, pois , desconsiderando o sinal de negativo temos a série harmônica.
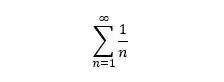
A série harmônica é uma série divergente, mas a série harmônica alternada converge quando aplicamos o teste da série alternada, então vemos que a série harmônica alternada é condicionalmente convergente, sacou?
E a gente finaliza esse conteúdo por aqui. Não é nenhum bicho de sete cabeças viu?
Além desse conteúdo em texto nós temos ele em vídeo também e você pode conferir bem aqui embaixo 👇🏽
Vídeo
Curtiu nosso conteúdo? Então assine com a gente para ter acesso a muito mais!
Teste da Série Alternada
Exercícios Resolvidos
Exercício Resolvido #1
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 677, exercício 11
Teste a série quanto a convergência ou divergência.
Passo 1
Como ele só pede para testar a convergência da série, não precisamos ficar pensando se ela será condicionamento ou absolutamente convergente.
Como temos o termo sabemos que é uma série alternada com
Então, partiu usar o teste das séries alternadas.
Passo 2
Como ver se é decrescente? Não podemos afirmar isso de cara, temos que calcular sua derivada e ver se ela é negativa. Sendo
Temos
Como estamos considerando apenas a parte onde é positivo, sabemos que quando :
Portanto, sabemos que em , a função acima é decrescente. Agora precisamos checar se tende a zero.
Logo, pelo Teste das séries alternadas, a série converge.
Resposta
A série converge.
Exercício Resolvido #2
PUC-RJ - Cálculo 3 - P3 2015.1 - 1b
b) Diga se a série abaixo converge ou diverge.
Passo 1
b)Para determinar que a série converge vamos usar o teste das séries alternadas. Primeiro vamos ver que
Onde é o termo geral da nossa série.
Para ver se a série converge temos que verificar duas coisas:
- é decrescente
Passo 2
Bom, vamos começar pelo começo:
Quero mostrar que é decrescente, para isso vamos fazer
Assim
Agora podemos ver se essa é decrescente, se ela for a nossa série também vai ser.
Para isso temos que olhar o sinal de
Passo 3
Agora vamos analisar o sinal de
O denominador é sempre positivo, no numerador temos uma função de grau, com , assim depois da segunda raiz ele vai ser negativo, assim:
E isso garante que é decrescente.
Passo 4
Para mostrar a segunda condição só temos que calcular o limite:
Bom,
Isso é uma indeterminação, vamos usar L’Hopital:
Continuou dando indeterminação, vamos usar L’Hopital de novo:
Portanto temos que a série converge.
Resposta
A série Converge
Exercício Resolvido #3
USP - Cálculo 4 - P1 2010 - 2b
Determine se a série abaixo é absolutamente convergente, condicionalmente convergente ou divergente:
Passo 1
Uma série alternada né galerinha? Vamos primeiro fazer o teste para ver se ela é absolutamente convergente, olhando essa cara, podemos comparar ela com uma função que conhecemos, mas teste da comparação não parece fácil de fazer. Mas podemos comparar ela com o teste da comparação no limite! Mas que função escolher? Ué, podemos aproveitar uma própria função que já tem nessa série : , sabemos que ela é uma p-série com , logo é divergente, então vamos ver isso daí:
Mas sabemos que , podemos substituir isso por :
Aplicando L’Hospital:
Logo a série não é absolutamente convergente!
Passo 2
Vamos usar o critério de Leibniz para verificar se ela é condicionalmente convergente, se você reparar na função , vai ver que ela é uma série descrecente, pois o valor da função vai caindo de acordo com o aumento de , mas repare também que o valor do logaritmo no limite é , ou seja, ela é limitada inferiormente, consequentemente ela é condicionalmente convergente pelo critério de Leibniz
Resposta
Condicionalmente Convergente!
Exercício Resolvido #4
USP - Cálculo 4 - P1 2013 - 2c
Determine se a série abaixo é absolutamente convergente, condicionalmente convergente ou divergente:
Passo 1
Bem, é uma série alternada, vamos ver se ela é absolutamente convergente. Mas antes temos que analisar o comportamento dessa função, nem sabemos se ela tende a quando , vamos ver isso daí:
Da pra substituir , então quando o
Assim fica:
Inderterminação de , logo, por L’Hospital:
Ok, o teste da divergência serve só quando o limite é diferente de , que aí afirmamos que ela diverge, vamos usar algum outro teste!
Passo 2
Vamos comparar com , já que ele aparece tanto na série, vamos fazer o teste da comparação no limite:
Fazendo a mesma substituição !
Por L’Hospital:
Novamente:
Então as séries tem o mesmo comportamente, como já sabemos que converge, concluímos que a série converge absolutamente pelo critério da comparação no limite!
Resposta
Converge Absolutamente