Modelagem de Problemas
Teoria
Introdução
Você já deve ter visto várias aplicações pra EDOs, agora a gente vai conversar sobre as aplicações de sistemas de EDO. Nós temos alguns casos que são bem característicos e vamos ensinar vocês a montar as equações de cada um desses casos.
A resolução nós não vamos falar nessa teoria, mas você vai perceber nas próximas teorias que se aprender a montar as equações direito a resolução sai de forma automática.
Os casos que vamos ver serão: sistema de molas acopladas, circuitos elétricos e mistura entre tanques.
Sistema de molas acopladas
Em um sistema de molas acopladas nós temos duas molas conectadas e queremos descobrir a deformação de cada uma delas em função do tempo. Tomando a figura abaixo com as molas e , com constantes e respectivamente, conectadas com os blocos de massa e . Seja a equação do deslocamento do bloco e a equação do deslocamento do bloco .
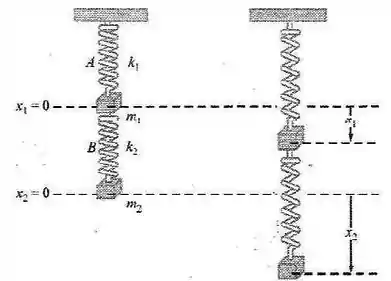
Agora vamos ter que usar aquele conhecimento de Física pra montar o nosso sistema de EDOs. Supondo que não temos nenhuma força externa, não tem a força da gravidade, no bloco de massa teremos uma força elástica da mola e uma da mola de forma que.
O sinal negativo da força da mola é por uma convenção de sinal. A deformação da mola vai ser o quanto o bloco desceu menos o quanto o bloco desceu.
Como nós só temos essas duas forças agindo no bloco de massa , pela segunda lei de Newton temos que.
Como
Nossas equações já estão começando a aparecer. No bloco de massa nós só teremos a ação da força , esse sinal negativo aparece porque no bloco a força puxava o bloco pra baixo enquanto no bloco ela puxa pra cima. De forma análoga ao que fizemos pro primeiro bloco nós obtemos a seguinte equação.
O nosso sistema fica então.
Agora já temos as equações pra essa aplicação.
Circuitos Elétricos
Essa é a parte mais chatinha porque tem bastante física, vou tentar simplificar bastante pra vocês pegarem a ideia do que tem que fazer pra resolver uma questão dessa.
Pra resolver esses problemas vamos precisar basicamente da primeira e da segunda lei de Kirchhoff. Vamos enunciar elas aqui embaixo e depois a gente vê direitinho num exemplo
Primeira lei de Kirchhoff
A primeira lei é a lei das correntes, ela diz que a soma das correntes entrando e saindo em um nó é igual a zero. Isso quer dizer que toda corrente que entra em um nó tem que sair também.
Segunda lei de Kirchhoff
A segunda lei é a lei das malhas, ela diz que a soma das forças eletromotrizes em uma malha é igual à soma das quedas de potencial. Essa é mais confusa, mas a ideia é simples. Resistores, Indutores e Capacitores geram variação de potencial quando uma corrente passa por eles, essa lei diz que a ddp entre dois pontos é a soma dessas quedas.
Antes de aplicarmos essas leis tem algumas decorebas que você tem que guardar sobre queda de potencial. Abaixo estão as fórmulas de como fica a queda de potencial quando uma corrente passa por um indutor, resistor ou capacitor
Você percebeu que só a formula do capacitor que tá com ao invés de né? Isso é porque a formula do capacitor é com carga, mas nós só temos que lembrar da seguinte relação entre carga e corrente que fica tudo certo.
Agora nós já temos as nossas leis e as nossas decorebas, vamos aplicar no circuito abaixo.
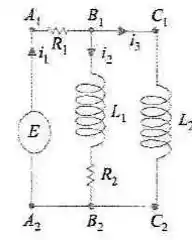
No nó nós temos corrente entrando e correntes e saindo ,então pela primeira lei de Kirchhoff.
Agora vamos usar a segunda lei. O potencial entre e é dado por , onde é uma função de um força eletromotriz. Pela segunda lei de Kirchhoff a gente sabe que esse também é igual a queda de potencial quando a gente analisa o caminho ou o caminho . Utilizando as nossas decorebas nós temos.
Agora nós podemos usar a equação que achamos com a primeira lei pra sumir com o e assim nós ficamos com as seguintes equações.
Conseguimos nosso sistema de EDOs
Mistura entre tanques
A ideia de problemas com tanques é bem simples. Vamos supor que temos dois tanques que possuem quantidades de um sal. Vamos definir as funções da quantidade de sal nos tanques como e . Vamos usar a figura abaixo pra ficar mais fácil de entender como funciona essa modelagem.
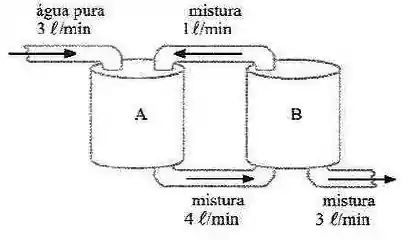
Vamos designar a nossa função pro tanque e pro tanque . A grande chave desses problema é lembrar que a variação da quantidade de sal, a derivada em função do tempo, vai ser igual a taxa de sal que entra menos a que sai. As taxas vão ser a concentração do sal vezes o fluxo de liquido. Sendo assim nós vamos ter.
Pra gente poder resolver o problema vamos supor que os dois tanques tem 20 litros de agua pura. Bora resolver então.
No tanque temos entrando agua pura e agua da mistura do tanque . A agua pura tem concentração de sal igual a 0 e a agua da mistura de tem concentração de , que é a quantidade de sal desse tanque dividida pelo volume dele. Temos saindo nesse mesmo tanque uma mistura com concentração de , que é a quantidade de sal desse tanque dividida pelo volume dele.
No tanque nós vamos ter aquela mistura que saiu do tanque entrando no tanque . Saindo nós vamos ter agora aquela mesma mistura que tava entrando em e agora uma outra saída, com a mesma concentração, que vai pra fora dos dois tanques como mostra a figura.
Bem simples né galera?
Circuitos Elétricos
Mistura entre tanques
Exercícios Resolvidos
Exercício Resolvido #1
Dennis Zill, Equações diferenciais volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2006, pp19-18
Estabeleça o sistema de equações dado abaixo a partir da figura.
Passo 1
Nessa questão vamos ter que usar os conhecimentos de física para montar as equações. Sabemos da primeira lei de Kirchhoff que
Para acharmos as outras equações vamos ter que analisar cada malha separada.
Passo 2
Analisando somente a malha que contem o indutor e o resistor . Pela segunda lei de Kirchhoff temos.
Já encontramos nossa primeira equação.
Passo 3
Analisando a malha geral. Pela segunda lei de Kirchhoff temos.
Como é a carga que está no capacitor e é a única corrente que passa pelo capacitor, temos.
Passo 4
Ao igualarmos as equações encontradas no passo 2 e 3.
Como nós sabemos que
Como sabemos que
Encontramos nossa segunda equação.
Resposta
Demonstramos como encontrar as equações a partir da figura.
Exercício Resolvido #2
Dennis Zill, Equações diferenciais volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2006, pp26-18
Considere dois tanques e com o líquido sendo bombeado para dentro e para fora às taxas mostradas na figura abaixo. Sendo o tanque contendo litros de água em que foram dissolvidos 25 gramas de sal e o tanque contendo litros de água pura. Qual é o sistema de equações diferenciais se, em lugar de água pura, bombearmos para dentro do tanque uma solução de salmoura contendo .
Passo 1
Esse é um caso clássico de tanque, Para resolver temos que lembrar daquelas equações bizuradas que vimos na teoria. Seja a concentração de sal no tanque e a concentração no tanque , Temos.
Passo 2
Vamos aos valores. No problema ele diz que entra no tanque água com concentração de a uma taxa de . Pela figura nós percebemos que também entra água vinda do tanque , essa agua vai ter uma concentração de que é a concentração de sal em dividido pelo volume total.
A taxa de saída do tanque vai ter a concentração de dividida pelo volume total, Como a taxa é de
Sendo assim.
Passo 3
Vamos tratar do tanque agora. O tanque só recebe água do tanque que vai ser igual a taxa de saída de que nós já calculamos.
A taxa de saída vão ser os dois fluxos que nós vemos na figura. Os dois tem a concentração de e as taxas como escrito na figura. Sendo assim.
Então a nossa equação fica
Passo 4
O sistema fica