Considere um sistema de potência simples consistindo em uma fonte ideal de tensão, um transformador elevador ideal, uma linha de transmissão, um transformador abaixador ideal e uma carga. A tensão da fonte é A impedância da linha de transmissão é e a impedância da carga é .
Assuma que os transformadores não estão presentes no circuito. Qual é a tensão da carga e a eficiência do sistema?
Assuma que o transformador é um transformador elevador e que o transformadoré um transformador abaixador . Qual é a tensão da carga e a eficiência do sistema?
Passo 1
Na letra ele pede para desconsiderar os dois transformadores. Então o circuito será:

Pela Lei de Ohm, a corrente na carga será:
Logo, a tensão da carga será:
Passo 2
Para calcular a eficiência do sistema, fazemos:
Lembrando que as perdas ocorrem da linha de transmissão, a potência de entrada será:
Logo, a eficiência será:
Passo 3
Na letra ele se refere ao circuito abaixo: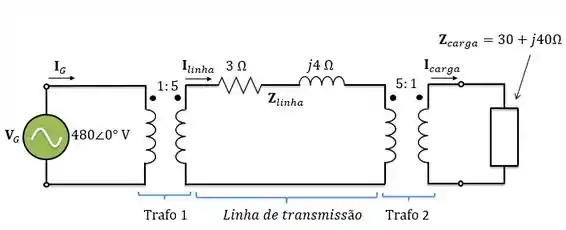
Como a gente quer saber a tensão em cima da carga, vamos refletir tudo para o primário do transformador 1.
A relação de transformação do transformador 1 é:
A relação de transformação do transformador 2 é:
Refletindo a carga do secundário para o primário do transformador 2:
Até então o circuito está assim:
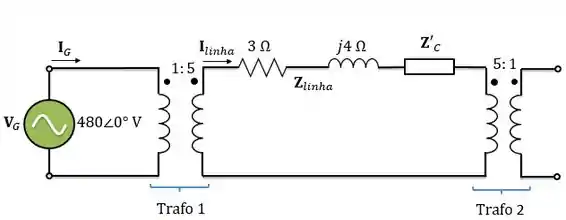
Agora, temos que refletir a impedância da carga novamente, mas desta vez para o primário do transformador 1 . Então:
Substituindo a equação na equação :
Logo:
Esse resultado é interessante, porque diz que a impedância do secundário do transformador 2 é igual à impedância refletida para o primário do transformador 1. Mas por que isso aconteceu?
Se a gente notar, as relações de transformação têm valores inversos. Isso faz com que, no final de tudo, elas simplifiquem. Então:
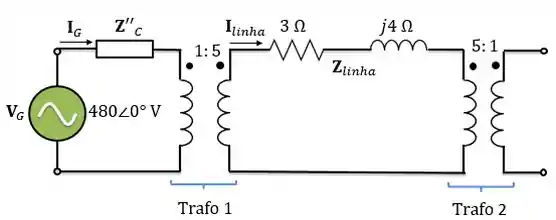
Passo 4
Agora falta a gente refletir a impedância da linha do secundário para o primário do transformador 1. Então:
Passo 5
Para calcularmos a corrente que circula no circuito abaixo, utilizamos a Lei de Ohm:
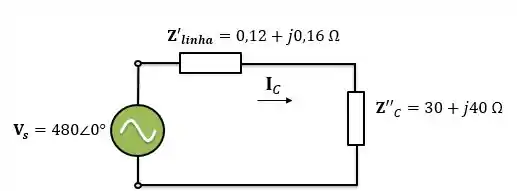
Passo 6
Logo, a tensão na carga será:
Passo 7
Agora vamos calcular a eficiência do sistema:
A potência de entrada tem que levar em consideração as perdas na linha de transmissão:
Portanto, a eficiência será: