Um gerador monofásico de alimenta uma carga através de uma linha de transmissão. A impedância da carga é e da linha é .
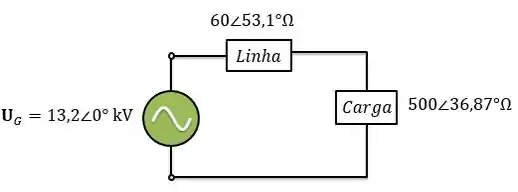
Se um gerador for conectado diretamente à carga como no circuito abaixo, qual é a razão entre a tensão da carga e a tensão gerada ? Quais os valores das perdas do sistema?
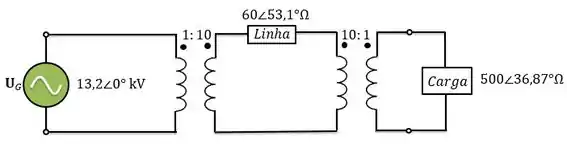
Se dois transformadores forem colocados no sistema conforme o circuito abaixo, qual será o valor da nova razão entre as tensões da carga e do gerador? Quais os valores das perdas no sistema agora? (Os transformadores podem ser considerados ideais)
Passo 1
Para fazer letra primeiro temos que encontrar a corrente do circuito:
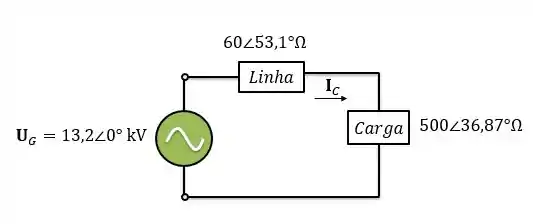
Pela Lei de Ohm, a corrente na carga será:
Passo 2
A tensão da carga será:
Passo 3
A razão entre a tensão da carga e do gerador será:
Isso significa que a tensão da carga é da tensão do gerador.
Passo 4
As perdas do sistema serão causadas pela resistência da linha de transmissão. Então:
A resistência da linha será:
Logo:
Passo 5
Para a letra precisaremos calcular a nova tensão em cima da carga.
Como a gente quer saber a tensão em cima da carga, vamos refletir tudo para o primário do transformador 1.
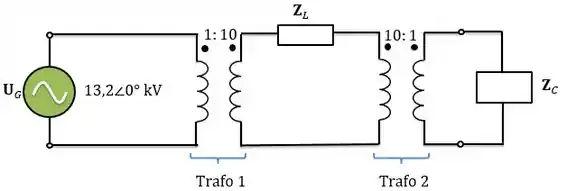
A relação de transformação do transformador 1 é:
A relação de transformação do transformador 2 é:
Refletindo a carga do secundário para o primário do transformador 2:
Até então o circuito está assim:
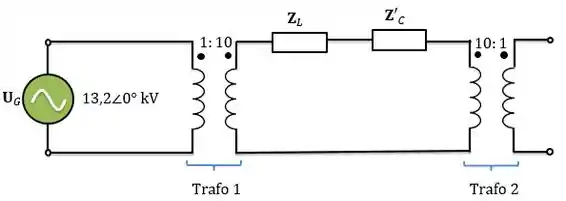
Agora, temos que refletir a impedância da carga novamente, mas desta vez para o primário do transformador 1 . Então:
Substituindo a equação na equação :
Logo:
Esse resultado é interessante, porque diz que a impedância do secundário do transformador 2 é igual à impedância refletida para o primário do transformador 1. Mas por que isso aconteceu?
Se a gente notar, as relações de transformação têm valores inversos. Isso faz com que, no final de tudo, elas simplifiquem. Então:
Ou, ainda:
Passo 6
Agora falta a gente refletir a impedância da linha do secundário para o primário do transformador 1. Então:
Ou, ainda:
Passo 7
Depois de fazer todas as reflexões necessárias, temos o seguinte circuito:
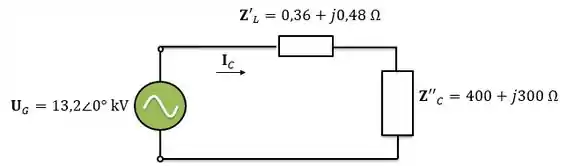
Pela Lei de Ohm, a corrente do circuito será:
Passo 8
Portanto, a nova tensão na carga será:
Passo 9
Após a conexão dos dois transformadores no circuito, a nova razão entre as tensões da carga e da fonte será:
Isso significa que a tensão da carga é da tensão do gerador.
Passo 10
As perdas do sistema serão causadas pela resistência da linha de transmissão. Então: