Classificação de Pontos Críticos em Funções de 2 Variáveis
Produzido por Bruno NeresTeoria
Agora chegou a hora de ver pra que diabos serve achar os pontos críticos de uma função. Assim como para funções de uma variável, isso vai servir pra achar os extremos da função.
Para uma variável, tínhamos três possibilidades quando a derivada era zero: máximo, mínimo ou ponto de inflexão (nem máximo nem mínimo), certo?
E aí fazíamos o teste da derivada segunda. Dependendo do sinal da derivada segunda, dava pra saber qual dessas opções era o caso.
Agora, temos um novo teste da derivada segunda. Ele vai ser nosso meio de classificar pontos críticos de funções de 2 variáveis.
Nosso teste da derivada segunda consiste, agora, em calcular o determinante da matriz hessiana, no ponto crítico de interesse e analisar o seu sinal.
Mas que diabos é matriz hessiana? É uma matriz com as derivadas de segunda ordem da função.
Então o que temos que fazer é calcular:
Chamamos esse determinante de hessiano, por isso a letra .
Ou seja:
Agora, dependendo do caso, o ponto pode ser um ponto de máximo, mínimo ou ponto de sela (nem máximo nem mínimo). Assim:
é ponto de máximo ou mínimo
Se é ponto de mínimo
Se é ponto de máximo
é ponto de sela
não se sabe
Por exemplo, para classificar os pontos críticos de
Primeiro temos que achar seus pontos críticos, igualando suas derivadas parciais a zero:
Portanto, o único ponto crítico da é o ponto .
Calculando derivadas segundas e substituindo em :
Repare que as derivadas segundas são constantes, elas não dependem das coordenadas do ponto. Mas se dependessem, era só fazer
Calculando :
Como , então este é um ponto de máximo ou mínimo. Para saber, basta analisar o sinal de . Temos que , então este é um ponto de máximo.
Aqui o gráfico da função:
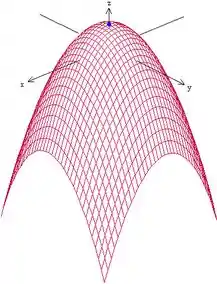
De fato podemos ver que o ponto é um ponto de máximo!
Método alternativo
Vamos dar uma olhada numa outra maneira de classificar pontos críticos de 2 variáveis. Se sua faculdade não cobra isso fique à vontade pra pular essa parte! ;)
Esse método envolve álgebra linear. Primeiro nós montamos a matriz hessiana do ponto crítico que estamos estudando, que nem fizemos agora a pouco. Mas agora vamos nos interessar nos autovalores dessa matriz hessiana:
- Se todos os autovalores são positivos então temos um ponto de mínimo
- Se todos os autovalores são negativos então temos um ponto de máximo
- Se os autovalores alternam entre positivos e negativos então temos um ponto de sela
Show? Vamos verificar pro exemplo lá de cima!
Achamos um único ponto crítico, , e sua matriz hessiana é:
Vamos agora calcular os autovalores dela. Para isso, precisamos resolver o determinante da matriz hessiana subtraída da matriz identidade, multiplicada por , e igualar esse determinante a zero. Ou seja:
Como temos dois autovalores negativos esse é um ponto de máximo. Que nem achamos antes!
Método alternativo
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, exemplo 4.4, p.131 (modificado)
Seja . Identifique e classifique o(s) ponto(s) crítico(s) de .
Passo 1
Calcular gradiente:
Passo 2
Encontrar pontos críticos:
Passo 3
Igualando as coordenadas:
Dividindo tudo por 2:
Pela segunda equação:
Substituindo na primeira equação:
Pela segunda equação novamente:
Então:
Então o único ponto crítico é .
Passo 4
Vamos analisar que tipo de ponto crítico é este:
Calculando derivadas segundas:
Passo 5
Calculando essas derivadas no ponto :
Passo 6
Calculando :
Como , então este é um ponto de sela.
Resposta
A função tem um ponto de sela em .
Exercício Resolvido #2
Cálculo 2 UNICAMP, Exame 2014 Noite, questão 2
Determine e classifique o(s) ponto(s) crítico(s) da função
Passo 1
Assim que a gente vir essas palavrinhas mágicas, “classifique os pontos críticos”, o nosso reflexo tem que ser: calcular as derivadas parciais, igualá-las a 0 e depois mandar ver no teste da derivada segunda! Então vamos fazer isso, começando pelas derivadas parciais!
Usando a regra da cadeia:
Passo 2
Show! Agora vamos igualar essas derivadas a 0:
Da segunda equação, tiramos
Substituindo na primeira, vai dar:
Beleza, então só tem um ponto crítico, o ponto .
Passo 3
Agora só resta classificar esse ponto crítico, usando o teste da derivada segunda, então vamos calcular as derivadas segundas! Lembrando que e . Assim,
Também temos:
E pras derivadas mistas:
Passo 4
Pronto! Agora podemos aplicar o teste da derivada segunda :) O nosso determinante vai ser:
Lembrando: como o ponto não é ponto de sela. Ele pode ser um ponto de máximo ou mínimo local, dependendo do sinal de .
Mas , portanto o ponto é um ponto de mínimo local.
Resposta
tem 1 ponto crítico: o ponto de mínimo local .
Exercício Resolvido #3
Cálculo 2 UFRJ, P2 2013.2, questão 2
A função possui
- Infinitos pontos de sela
- Infinitos pontos de máximo local
- Infinitos pontos de mínimo local
- Exatamente um ponto de mínimo local e um de máximo local
- Nenhuma das outras alternativas
Passo 1
Devemos começar achando os pontos críticos. Primeiro vamos calcular as derivadas da função
Então os pontos críticos são aquele que
Passo 2
Da segunda equação temos
Com sendo um número inteiro.
Dessa forma na primeira equação temos
O cosseno vai ser sempre diferente de zero, logo
O ponto crítico é
Com sendo um número inteiro.
Passo 3
Agora devemos calcular o determinante de
Vamos primeiro achar as derivadas segundas
Passo 4
Substituindo os valores dos pontos críticos vamos encontrar
Passo 5
Voltando ao determinante
Como
Vamos ter
Então todos os pontos críticos são pontos de sela, e teremos infinitos pontos de sela.
Resposta
Alternativa (a)
Exercício Resolvido #4
Cálculo 2 USP, P3 2010, questão 2
Seja em que e são números reais não nulos. Encontre os pontos críticos de e classifique-os em função de e .
Passo 1
Partiu encontrar os pontos críticos! Sabemos que esses pontos ocorrem quando as derivadas parciais dão , certo? Sendo assim, calculemos essas derivadas!
Derivando em relação a , usamos a regra do produto:
Ou seja, a derivada de , vezes , mais vezes a derivada de !
Agora, derivemos em relação a :
Para isso, apenas tratamos o como constante e usamos a regra da cadeia ;)
Passo 2
Próximo passo, igualar cada derivada a !
Como temos esse termo com o igual duas vezes, coloquemos em evidência:
E agora, vemos que a única maneira de zerar essa equação é quando o termo entre parêntesis dá , pois não importa o número que elevemos , ele nunca será ! Para isso, temos que , e então ;)
Passo 3
Fazendo o mesmo processo para a derivada em relação a , temos:
Para essa equação ser zerada, temos que , ou , certo? Porque, novamente, o termo com o não vai ser nunca.
Olha a nossa função inicial,
Repara que , isso porque tem uma divisão com ali, então não pode ser ponto crítico.
Assim, nosso único ponto crítico fica sendo !
Passo 4
Beleza, agora que temos o ponto crítico, como classificá-lo? Precisamos da matriz com as segundas derivadas, certo? Então, antes de mais nada, cadê essas derivadas? Vamos encontrá-las!
Derivando novamente em relação a , teremos:
Derivando cada termo da diferença acima, temos:
Fazendo essa distributiva do , temos:
Como os dois primeiros termos são iguais e de sinais opostos, cortamos eles! Por fim,
Show! Derivadas em relação a estão aí :)
Passo 5
Agora, derivemos a em relação a novamente:
Apenas usando a regra do produto,
Ok.. não parece ter muito mais coisa pra fazer hehehe
Só pro passo não ficar curto além da conta, vamos encontrar as derivadas mistas? Lembrando que , podemos escolher, entre derivar em relação a a , ou derivar em relação a a ! Fiquemos com a primeira opção :]
Colocando o termoem evidência,
Passo 6
Como o nosso , candidato a máximo, mínimo ou ponto se sela, é , coloquemos esses valores para e em cada uma das segundas derivadas para ver o valor que elas assumem!
Para a segunda derivada em relação a , temos:
Para a segunda derivada em relação a , temos:
Como o termo ,
Para as derivadas mistas, temos:
Como o termo ,
Passo 7
Beleza, agora é preencher o determinante!
Agora temos que analisar esse resultado...
Como o termo com o será sempre positivo, caso , então o determinante é menor que , e o é ponto de sela!
Caso , temos a opção de também. Nesse caso, teremos o determinante maior que , e o , então, teríamos um ponto de mínimo local!
Caso , temos a opção de . Nesse caso, teremos o determinante maior que , e o , então, teríamos um ponto de máximo local!
Resposta
- Caso , então o determinante é menor que , e o é ponto de sela!
- Caso , temos a opção de também, então, teríamos um ponto de mínimo local!
- Caso , temos a opção de também, então, teríamos um ponto de máximo local!
Exercício Resolvido #5
Cálculo 2 CEFET-RJ, P1 2014.2 Prof. Péricles Aguiar, questão 3
Um fio de arame com de comprimento será cortado em 3 pedaços. Um deles será encurvado na forma de uma circunferêcia, outro na forma de um quadrado, e o terceiro na forma de um triângulo equilátero. Como deve ser cortado o fio para que a área combinada das três figuras seja a maior possível?
Passo 1
Certo, vamos simplificar o problema. Temos uma função , que é o comprimento do fio e outra Área Total, que queremos encontrar o ponto extremo dela. Então, vamos lá! Comecemos encontrando a função :
Em que , e são os tamanhos os quais o fio foi cortado. Isso significa que, na verdade, , e são os perímetros das figuras!
Passo 2
Agora, o que acha de definirmos a função ?
Em que é a área total, é a área do círculo, é a área do quadrado e é a area do triângulo.
Passo 3
Então, chegou a hora de definir quais são as áreas e comprimentos que formam a área e o perímetro totais:
Em que R é o raio da circunferência
E é o perímetro do círculo
Em que é o lado do quadrado
E é o perímetro do quadrado
Em que s é o lado do triângulo
E é o perímetro do triângulo
Lembrando que , e são os tamanhos em que o fio foi cortado (ou seja, os perímetros das figuras)!
Passo 4
Pronto!! Agora que você já aguentou até aqui, segura mais um pouco que chegou a parte fácil!
Encontramos as áreas em função de , e , certo? Então vamos reescrever a função Área Total:
Aqui vem uma pequena modificação na função. Sabemos que , e são os tamanhos dos cortes no fio. Então:
Assim, podemos isolar uma das variáveis. Vamos isolar o
E, finalmente, substituimos esse valor de na equação
Ótimo, temos a função Area Total exatamente como era pra ser :) Ela está agora em função de apenas duas variáveis.
Passo 5
Para encontrar o pontos críticos de vamos começar encontrando suas primeira e segundas derivadas parciais:
Derivando em relação a e igualando a derivada a 0...
Derivando em relação a e igualando a derivada a 0...
OBS: Estamos igualando a Derivada a porque temos que encontrar os pontos críticos!
Derivando em relação a ...
Derivando em relação a ...
E, por último, derivamos uma das primeira derivadas em relação a outra:
Passo 6
Tendo as derivadas parciais, vamos fazer o teste da segunda derivada:
E o importante não é o resultado, mas sim, sabermos de ele é maior, menor ou igual a . Este, é maior que ! Isso significa, que, para qualquer e qualquer , teremos um ponto de mínimo!
Passo 7
A partir das equações das primeiras derivadas, temos:
Então,
logo,
Passo 8
Legal, encontramos uma relação entre e . Com ela, basta que substituamos esse valor de em função de em uma das equações da primeira derivada.
Como ...
Isolando o ...
Passo 9
Finalmente!! Conseguimos o tamanho de um dos cortes em função do comprimento total ! Agora, vamos encontrar o outro com a nossa relação entre e :
Então...
E agora, só falta o perímetro do triângulo, :
Resposta
As expressões para os três cortes podem ser dadas em função do comprimento total por:
Círculo:
Quadrado:
Triângulo: