Ponto Crítico de Uma Função de Várias Variáveis
Teoria
Heeey! Seja muito bem vindo ao Responde Aí! Bora bater um papo sobre Ponto Crítico de Uma Função de Várias Variáveis?!
Vamos direto ao ponto, sem enrolação!
Os pontos críticos de uma função de várias variáveis são aqueles onde as derivadas parciais valem zero, ou pelo menos uma delas não existe.
Agora que a gente já sabe o que é um ponto crítico de uma função, podemos aprender como achar!
Como achar os pontos críticos de uma função?
Vamos relembrar como que calculávamos o ponto crítico de funções com apenas uma variável! Se liga no exemplo a baixo:
Calculamos a derivada dessa função:
Igualamos a derivada a zero:
Podemos confirmar olhando seu gráfico:
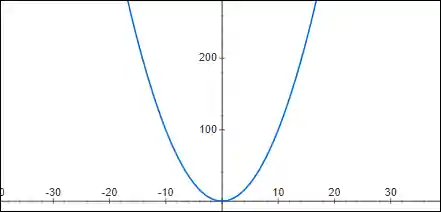
Molezinha, não é?!
Agora vamos aprender como achamos os pontos críticos em funções de duas variáveis!
Ponto crítico de uma função de duas variáveis
Já vamos começar com um exemplo:
Calculamos as derivadas parciais de
Pra um ponto ser um ponto crítico pelo menos uma delas não pode existir, ou todas elas têm que valer zero.
Assim, ficamos com o sistema:
Substituindo a segunda equação na primeira, ficamos com:
Logo
Portanto,
Bora pra mais um exemplo então!
Arrumando a casa:
Igualando a primeira equação à zero:
Agora a segunda equação:
Como a nossa exponencial nunca da zero para um número real, temos que:
Como já vimos que
Logo, nossos pontos críticos são:
E é só isso!
Mas se você quiser, também temos esse conteúdo em vídeo, confere aqui em baixo:
Partiu exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, exemplo 4.4, p.131 (modificado)
Seja . Identifique o(s) ponto(s) crítico(s) de .
Passo 1
Calcular gradiente:
Passo 2
Encontrar pontos críticos:
Passo 3
Igualando as coordenadas:
Colocando em evidência:
Pela segunda equação:
Substituindo na primeira equação:
Pela segunda equação novamente:
Então:
Então o único ponto crítico é .
Resposta
A função tem um ponto crítico em .
Exercício Resolvido #2
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, p. 358 (modificado)
Mostre que é um ponto crítico de , não importando o valor da constante .
Passo 1
Vamos calcular as derivadas parciais da :
Passo 2
No ponto , as derivadas parciais valem:
Então o valor de realmente não importa: de qualquer forma as derivadas parciais se anulam!
Portanto, o ponto é um ponto crítico de .
Resposta
pra qualquer .
Exercício Resolvido #3
Cálculo 2 PUC-RJ, P2 2013.2, questão 1 (modificada)
Considere a função
Encontre todos os pontos críticos de .
Passo 1
Vamos calcular as derivadas parciais da , usando a regra do produto e a regra da cadeia:
Botando em evidência:
E pra derivada parcial em relação a temos
Agora botamos em evidência:
Resumindo:
Passo 2
Agora vamos zerar as derivadas parciais.
A exponencial nunca vale zero, então temos
Passo 3
Subtraindo a 2ª equação da 1ª:
Passo 4
Beleza, agora substituímos numa das equações que achamos:
Show, estamos quase acabando.
Passo 5
Se , então . E se :
Então a função tem 2 pontos críticos: os pontos e .
Resposta
e
Exercício Resolvido #4
Cálculo 2 UFRJ, P2 2014.2, questão 4
Suponha que a função tem um ponto crítico em no espaço. Se e são números reais positivos, então a função tem um ponto crítico em
(a)
(b)
(c)
(d)
(e) a informação é insuficiente
Passo 1
Essa é uma questão mais teórica, mas você vai ver que não tem mistério!
é um ponto crítico de , ou seja nesse ponto as derivadas parciais se anulam, ou uma delas não existe, certo?
Vamos primeiro considerar que as derivadas parciais valem zero:
Agora vamos dar uma olhada na função :
Repare que as derivadas parciais da são as derivadas parciais da multiplicando ! O , constante, some. Pelas regras básicas de derivação, temos:
Passo 2
E no ponto as derivadas parciais da são todas iguais a zero né?? Ótimo, então elas também vão ser zero pra :
Então nesse caso o ponto também é um ponto crítico da !
Passo 3
Agora vamos ver o caso em que é um ponto crítico da porque uma das derivadas parciais não existe.
Quando dizemos que a derivada parcial não existe é porque ela não é definida nesse ponto. Vamos supor, por exemplo, que a derivada parcial de em relação a não existe. E, como já vimos:
Ou seja:
A só é a multiplicada por uma constante, então ela também não existe!
Portanto, em qualquer um dos casos o ponto é ponto crítico da .
Resposta
Alternativa (a)