Calcule a integral do campo vetorial ao longo da curva interseção da superfície , com o plano , orientada no sentido de crescimento de .
Passo 1
O enunciado pede a integral do campo vetorial ao longo de uma curva né? Sabemos que o que ele está pedindo, em outras palavras, é isso aqui
Vamos tentar visualizar nossa curva pra ver qual a melhor forma de calcular isso, ele quer a interseção dessas duas superfícies aqui
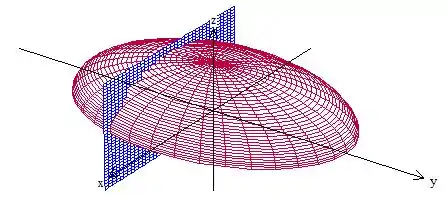
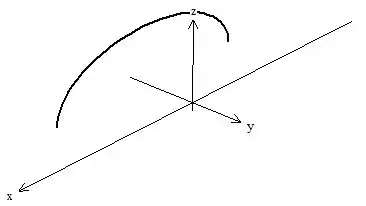
É uma curva aberta, certo? O problema é que esse campo é muito complexo pra gente resolver a integral de forma direta, vamos ter que aplicar algum teorema aqui. Primeiramente, vamos ver como é o rotacional de , às vezes isso facilita o exercício
Que beleza, o rotacional é nulo! Podemos então tentar aplicar o teorema de Stokes, pra isso vamos fechar essa curva ai. O jeito mais fácil é simplesmente ligar as extremidades da curva , fica assim
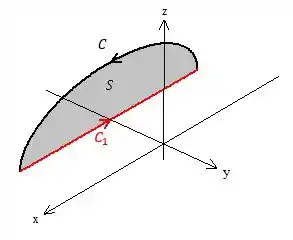
O teorema de Stokes fica assim
Como o rotacional é nulo, essa integral dupla fica igual a zero, portanto
Precisamos só calcular essa integral da curva !
Passo 2
Pra calcular essa integral de linha, vamos precisar de uma parametrização da reta , ela liga os pontos extremos da curva aberta , mas que pontos são esses?
Esses pontos pertencem a elipse
E aos planos e , portanto
Portanto os pontos são
Passo 3
A reta que queremos parametrizar começa em positivo e termina em negativo, não é? Então essa reta pode ser parametrizada por
Beleza, tendo a parametrização da reta, vamos ver como fica o campo nesses novos parâmetros
Passo 4
Agora é só juntar tudo na integral
Passo 5
Agora é só voltar lá pro que montamos nos teorema de Stokes