Calcule a integral de linha de campo vetorial onde é a curva definida como interseção, no primeiro octante, do cilindro com o plano , e o campo
Escolhe e indique a orientação da curva .
Passo 1
Bom, já viu que a expressão desse campo é zoadaça né, sem condições de resolver isso aí pela definição, vamos tentar Stokes.
Começamos calculando o rotacional para ver no que dá:
E, como o campo está definido em todo o , podemos dizer que ele é conservativo e tudo fica lindo :D
Passo 2
Beleza, agora vamos dar uma olhada na curva , que é dada pela interseção de:
Graficamente é isso aqui:
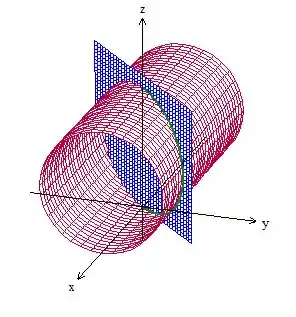
A curva é essa elipse onde as superfícies se cortam. Como a curva se limita ao primeiro octante, temos isso aqui:
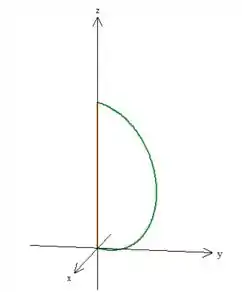
O problema pediu para a gente orientar , vamos parametrizar em coordenadas polares deslocadas com :
Vamos orientar de a , ou seja, do plano , sentido anti-horário.
Para entender os intervalos, precisamos imaginar que o arco está centralizado (porque a nossa parametrização “fez” isso). Temos, então:
Passo 3
Agora, para aplicarmos Stokes, precisamos fechar essa curva e definir uma superfície.Vamos fechar com esse segmento de reta que une os ponto inicial e final mesmo:
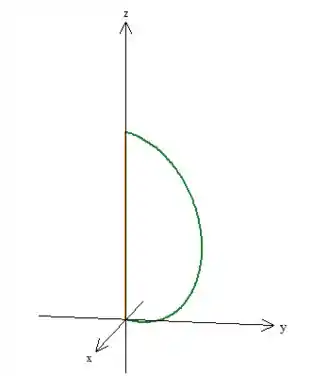
Para manter a orientação que demos ao arco:
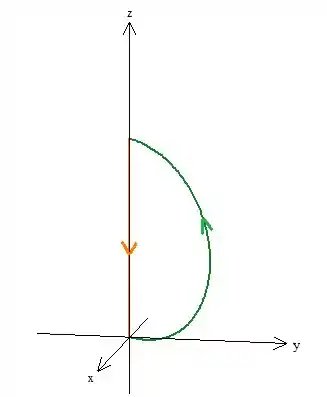
Então, podemos aplicar o teorema;
Onde é qualquer superfície que tenha a figura acima como fronteira.
Passo 4
Para calcular a integral no segmento, precisamos, antes de tudo, parametrizá-lo.
Como ele é paralelo ao eixo e tem , podemos escrever:
Onde vai de a (veja o desenho). Agora, derivamos isso aí:
Aplicando a fórmula:
O que nos dá:
Passo 5
Temos então: