Calcule a integral de linha vetorial , onde
E é a intersecção, no primeiro octante, do cilindro e com o plano , do ponto inicial até o ponto final . (Obs.: e
Passo 1
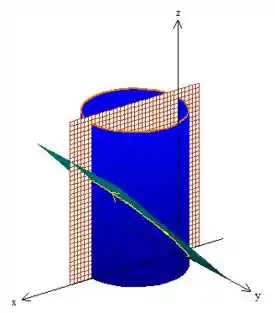
Para a gente ter uma noção clara do que vamos ter que fazer, é legal a gente ter uma boa visão de , certo? Então me acompanha aqui!
Bem... é a intersecção do cilindro com o plano . E esse cilindro está deslocado uma unidade em , se lembra?
Completando quadrado...
Fazendo a intersecção com o plano que é um plano paralelo ao eixo , e lembrando que queremos apenas o primeiro octante, obteremos a em amarelo. :D
Passo 2
Podemos ver que resolver aquele integral de linha direto pode nos dar muita dor da cabeça! Logo a gente vai recorrer a um método alternativo: ao teorema de Stokes que nos diz o seguinte
Onde
- é a borda de uma superfície fechada
- são os vetores normais a orientada positivamente
- é o rotacional do campo não singular (o campo que temos é não singular!:D)
Passo 3
Começando pelo , devemos escolher uma superfície fechada que tenha como borda, justamente a curva que queremos simplificar.
Ora! A superfície mais simples que faz isso é justamente a que está em cima do plano que delimita
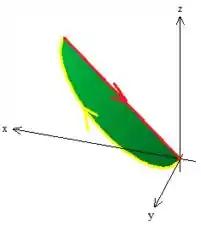
Cuidado! Essa orientação de toda borda deve ser a mesma pedida no exercício, okay?
Logo, do primeiro lado da equação de Stokes acima, teremos :
Portanto, pra gente encontrar o resultado que a gente quer, vamos calcular essas outras duais integrais aí e ver no que dá! :)
Passo 4
Vamos começar com a integral de superfície, e, portanto, a parametrizando.
Como a superfície está delimitada pelo cilindro, podemos pensar em uma parametrização em coordenadas cilíndricas (Mas lembre-se!: o cilindro está deslocado)
Como na superfície ,
Logo,
Onde varia até chegar o raio máximo do cilindro e dá uma meia volta, ou seja,
Passo 5
Vamos prosseguir calculando o .
Lembrando da fórmula da rotacional de um campo e calculando as integrais a gente vai ter
Ótimo! O rotacional realmente simplifica a nossa vida. Vamos ver se o vetor normal faz o mesmo?
Calculando essas derivadas parciais da superfície
E jogando no determinante esses vetores e;
Calculando... vamos obter
Observe que precisamos de mudar o sinal do vetor normal porque a curva está orientanda negativamente, logo, pela regrada mão direita precisamos da coordenada negativa, ou seja
Passo 6
Jogando tudo na integral de superfície e resolvendo o produto interno do rotacional com vetor normal:
Note que a única coordenada que nos interessa é a primeira e a última, pois elas não vão zerar, porém... precisamos mudar as coordenadas e para as coordenadas polares
Em a gente mata a integral mole e em é um polinômio, logo a gente mata fácil
Passo 7
Agora falta pra gente a integral de linha , que eu prometo ser mais simples!;)
Vamos começar parametrizando essa curva que é uma reta onde e , pois ela está em cima do plano
Logo
Onde então vai de até , pois queremos que a reta vá do ponto até o !
Agora derivando a superfície para obter o termo
Bem... não esquecendo de aplicar no campo vetorial a parametrização, podemos, por fim, ir para a integral
Resolvendo esse produto interno...
Conforme prometido, está aí! ;)
Passo 8
Agora voltando para o nosso problema e substituindo tudo nas integrais...