Calcule onde é a curva parametrizada por , e o campo
Passo 1
Vamos lá galera, fazer essa integral de linha diretamente parece impossível, né? Vamos tentar outra estratégia aqui. Perceba que a curva é aberta, ela tem esse formato aqui
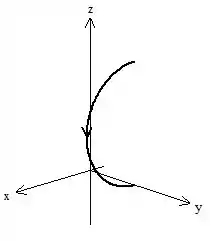
Se não podemos calcular direto, vamos tentar fechar essa curva e usar o teorema de Stokes, perceba que o rotacional desse campo é bem simples
Vamos então fechar com a reta que liga as extremidades dessa curva! Assim olha
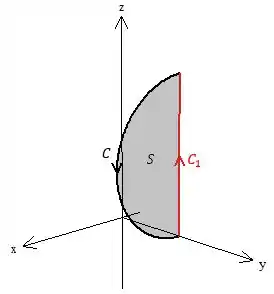
O teorema de Stokes fica
Precisamos então só calcular a integral dupla e a integral de linha de , vamos lá?
Passo 2
Vamos começar com a integral de superfície, ela é uma superfície contida no plano , certo? Com isso a normal é fácil de ser encontrada! Se você não lembra, a normal de um plano qualquer
No nosso plano , temos que , e , portanto
Lembrando que o rotacional calculado lá no passo 1 é esse aqui
A nossa integral de superfície fica isso aqui então
Que beleza! A área da superfície facilita muito! Perceba que a nossa superfície é metade da área de um círculo de raio ! Portanto
Passo 3
Vamos agora para a nossa integral de linha da curva
Precisamos de uma parametrização dessa reta, não é? Ela liga as extremidades da curva , vamos descobrir quais são esses pontos
Então a nossa reta é constante em e , podemos parametrizá-la como
Beleza, substituindo esses valores no campo ficamos com
A derivada da parametrização é essa aqui
Portanto a integral de linha fica isso aqui
Passo 4
Agora é só voltar lá pro que montamos no teorema de Stokes