Teorema de Stokes, Integral de linha – caso vetorial
Seja a curva em parametrizada por . Seja
um campo vetorial em . Calcule a integral de linha do campo vetorial ao longo de .
Passo 1
A curva é alguma coisa desse tipo.
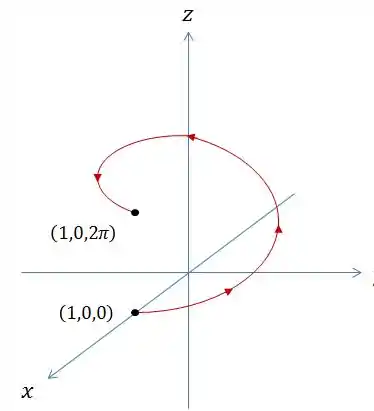
A gente pode até usar a parametrização que o problema nos deu e tentar resolver isso aqui por uma integral de linha de um campo vetorial, mas tá vendo como essa função é escrota?!
Então provavelmente tem uma outra forma de resolver isso.
Se a curva fosse fechada, nós poderíamos usar o Teorema de Stokes pra resolver o problema, certo?
Então porque não fechamos essa curva?!
Po, mas como assim?!
Se liga, se o Teorema de Stokes calcula a integral de linha sobre uma curva fechada , ela calcularia a integral de linha sobre a curva que é o que queremos, mais a integral de linha sobre a curva que vamos usar pra fechar, que vamos chamar de .
Basicamente, o que acontece é o seguinte:
Passo 2
Imaginando qual curva seria melhor pra fechar a curva , o que vem logo à cabeça é uma linha ligando os pontos inicial e final de .
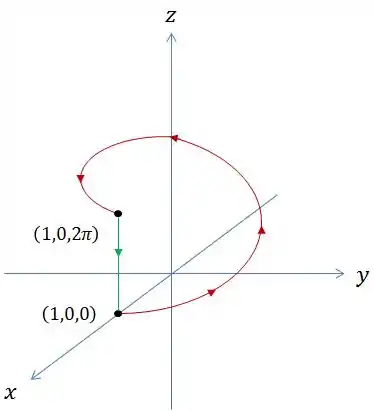
E parece curva boa porque, nela, o e o permanecem constantes e só o varia.
Repara que essa nova curva vai de à , estamos ligando o ponto final ao inicial para fechar essa curva, pode parecer estranho que agora a reta vai ter mudado a ordem mas é isso mesmo que acontece quando fechamos uma curva.
Pelo teorema de Stokes aqui, a nossa superfície é o interior dessa curva aí, é meio difícil imaginar, mas como a curva é fechada, ela tem uma superfície que podemos usar o teorema, beleza?
Bom, vamos pros cálculos.
Passo 3
De acordo com o Teorema de Stokes:
Vamos começar calculando o rotacional de .
Show de bola! Então é um campo conservativo! Isso vai facilitar a nossa vida! :D
E a integral de linha de um campo conservativo sobre uma curva fechada é SEMPRE igual a zero.
Portanto:
Passo 4
Vamos começar parametrizando a nossa curva.
Nela, como podemos ver no gráfico, e permanecem constantes e somente varia. Como temos que seguir o sentido da trajetória, os pontos inicial e final da curva são:
Então uma parametrização que parece boa é a seguinte:
Passo 5
Para montar a integral, precisamos saber quem é e .
Passo 6
Agora podemos montar a integral
Voltando pra integral: