Sejam e a interseção de e , percorrida de a . Calcule
Passo 1
Precisamos calcular uma integral de linha, né? Mas percebe que, mesmo que façamos uma parametrização fácil de , nosso campo tem um termo de , com certeza não vai ser simples de integrar isso ai. Vamos então tentar aplicar o Teorema de Stokes, lembra como ele é?
Portanto, vamos precisar calcular o , achar os limites de e, caso seja uma curva aberta, vamos ter que fechar com uma curva simples! Vamos verificar isso então, nosso esboço é assim:
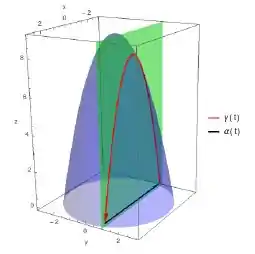
Sendo que a curva que estamos interessados é a vermelha, que é aberta. Precisamos fechar com a reta azul, que vai de a . Portanto, se chamarmos nossa curva azul de , nosso Teorema de Stokes fica:
Passo 2
Vamos começar então calculando nosso primeiro termo, para isso, vamos achar o , em seguida a normal e por fim os limites de integração. Bastante coisa né? Vamos passo a passo então.
A fórmula do rotacional é essa aqui:
Vamos fazer cada um com calma, nosso campo é esse aqui:
Com isso, nosso rotacional fica assim
Nossa superfície está inteira no plano né? Então é bem simples fazer essa parametrização aqui:
Tendo a parametrização, nosso rotacional com os novos parâmetros fica:
Passo 3
Nossa normal é calculada pelo seguinte produto vetorial:
Onde
Passo 4
Para calcular os limites da nossa superfície vamos ver a nossa equação escrita com os novos parâmetros:
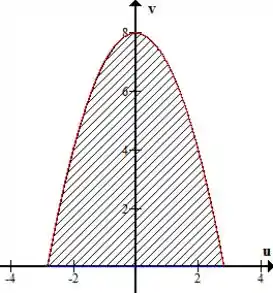
Passo 5
Juntando tudo isso na integral de superfície:
No nosso produto escalar quase tudo vai zerar! Nossa integral vai ficar assim então:
Integrando em :
Integrando em :
Passo 6
Falta agora só a gente calcular a integral de linha da reta que usamos para fechar a curva , né? Vamos ter que calcular isso aqui:
Onde é a reta que liga a , é ao contrário mesmo! Nossa parametrização vai ficar assim:
Nosso campo escrito com essa nova parametrização fica assim:
Passo 7
Substituindo tudo na integral:
Passo 8
Para acabar com a questão, voltando para o nosso Teorema de Stokes, tínhamos que:
Onde
Com isso, nossa resposta fica: