Calcule a soma dos módulos dos autovalores da matriz

Belezoca pra gente encontrar os autovalores de uma matriz, resolvemos a seguinte equação:

Onde é a matriz diagonal que possui os autovalores na diagonal principal:

Portanto queremos que o determinante dessa diferença seja igual a :

Então se a gente calcular esse determinante, os valores de que satisfazerem a igualdade, serão nossos autovalores.

Mas agora que vem o bizu matador das galáxias, porque pra calcular esse determinante, a gente pode separar essa matriz por matrizes em blocos, desse jeito:

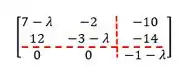
Agora a gente dividiu nossa matriz em matrizes distintas e :

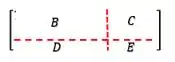
Onde temos:

E o determinante dessa matriz, pode ser calculado como se fosse um determinante de matriz , multiplicando os termos em forma de cruz, tipo assim:

E o legal da gente fazer essa divisão, é que se a gente reparar na matriz, vemos que é uma matriz formada somente de zeros:

Isso quer dizer que o produto vai ser igual a :

Tal que nosso determinante se resume ao produto entre:

Agora que a gente viu que podemos separar esse determinante em blocos, vamos dividir cada um deles pra gente calcular separado, saca só:

Então para o primeiro determinante, temos:

Ainda podemos reorganizar essa equação do segundo grau, como um produtinho notável, desse jeito:

Iradoso, e para o outro determinante, obtemos:

Portanto, temos que na verdade o determinante da matriz , é dado por:

E como queremos igualar esse limite a zero, fazemos:

Logo, nossos autovalores são:

E como queremos a soma do módulo deles, fazemos:

Meczada, então nossa resposta certa é a letra (a).