Encontre a solução do problema de valor inicial dado. Esboce o gráfico da solução e descreva seu comportamento quando aumenta.
Passo 1
Vamos começar então lembrando que devemos trocar nossa EDO pela equação auxiliar, certo? Onde trocamos
Ficamos então com
Resolvendo essa equação do segundo grau teremos inicialmente para o delta
Onde esses são os termos da equação do segundo grau, na forma
Observamos então que
Tranquilo? Bora calcular nosso delta então
Passo 2
Bom, haverá duas soluções para nossa equação. Supondo então que nossa solução é dada por , temos que nossa solução geral será
e
Ficando com e . Substituindo em nossa EDO, temos que
Caímos em uma equação de segundo grau. Resolvendo pelo método de Bhaskara, chegamos que
Presta atenção aqui que nosso delta é positivo. Teremos diferentes tipos de soluções de acordo com o delta, lembra? As possíveis soluções são
Já sabemos que nosso delta é positivo! Vamos agora calcular o valor de
Tendo como raízes e . Assim, temos que nossa solução geral para a EDO dada é (já que o delta é maior que zero)
Nós já temos os valores de e , então agora é só ser feliz substituindo no formato acima:
Passo 3
Aplicando as condições de contorno (para podermos descobrir os valores das constantes), temos
Logo,
Para derivar isso vamos aplicar a regra do produto no produto com o e no produto com o .
Bora lá então, agora vamos substituir os valores iniciais pra descobrirmos o valor das constantes. O enunciado nos deu
Então temos
Lembrando que o exponencial de zero vale 1, certo??
Agora pra a derivada
Opa, temos duas equações e duas incógnitas! Isso significa que conseguimos descobrir o valor dessas constantes aí montando um pequeno sistema de equações:
Se nós multiplicarmos a segunda equação por (-1), teremos
Agora somamos as duas equações
O que nos dá
Opa, já temos o valor de então já podemos descobrir o basta substituir em uma das duas equações que temos.
Passo 4
Maravilha! Já temos então o valor das duas constantes. Agora é só substituir na solução que tínhamos.
Assim nossa equação que satisfaz a EDO é
E o gráfico é algo desse tipo
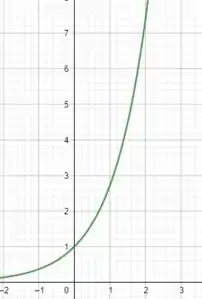
onde com o aumento de , aumenta exponencialmente. Tranquilo???