Circuitos Trifásicos
Produzido por Alexandre NunesTeoria
Hoje a gente vai conversar sobre os circuitos trifásicos, quando as fontes de tensão estão conectadas com a carga. A gente vai ver que há várias formas de fazer essa conexão e vamos fazer exemplos para ver como funciona!
Bora lá?!
Circuito Trifásico: Conexão Estrela-Estrela (Y-Y)
Um sistema estrela-estrela equilibrado é formado por uma fonte trifásica em estrela equilibrada ligada com uma carga em estrela também equilibrada, como no exemplo abaixo:
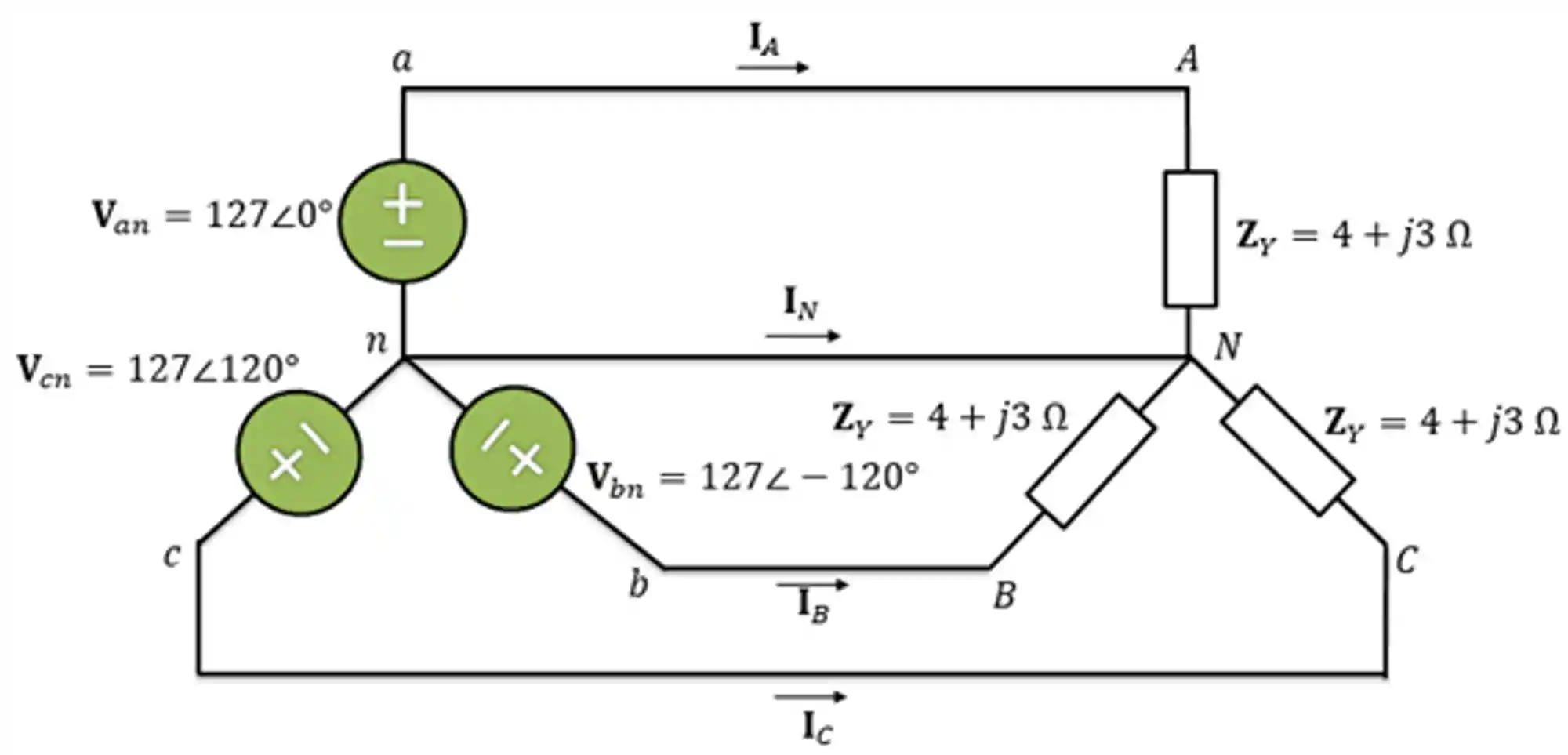
Para esse circuito, vamos calcular as correntes de linha, a corrente que passa pelo neutro e as tensões de linha. Mas não precisa se preocupar, vamos aprender no passo a passo!
📢 Clique para ver mais:
Passo 1: Encontrar as Correntes de Linha
Como o circuito trifásico é equilibrado, para encontrarmos as correntes de linha podemos analisar apenas uma fase, já que em todas as fases o módulo da corrente será o mesmo.
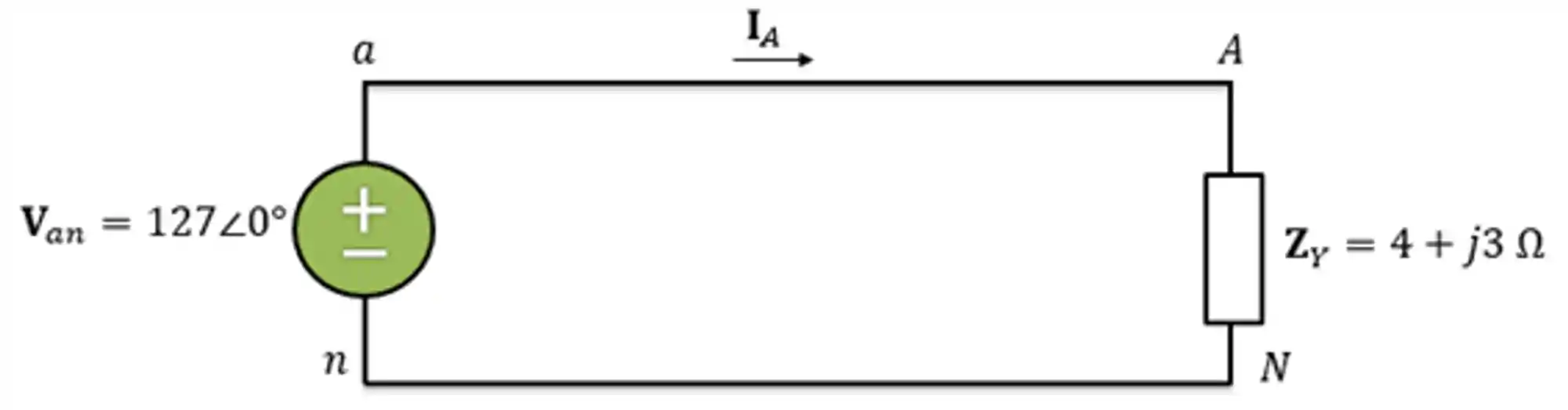
Pela lei de Ohm:
Para o nosso caso temos:
Substituindo e calculando:
Analisando as fontes de tensão, vemos que elas estão na sequência abc. Então, as correntes de linha também estarão na sequência positiva. Na fase b, temos:
E na fase c:
Passo 2: Encontrar as Correntes que passam pelo Neutro
Para calcular a corrente que passa pelo neutro, vamos utilizar a boa e velha lei das correntes de Kirchhoff no neutro:
Isso mesmo! Não circula corrente pelo neutro em um circuito Y-Y equilibrado! Por isso, podemos eliminar a ligação entre o neutro da fonte e da carga.
Passo 3: Calcular as tensões de linha
Agora, vamos calcular as tensões de linha. Sabemos que na ligação estrela temos a seguinte relação entre os módulos da tensão de linha e de fase:
Logo:
Como o sistema é equilibrado, todas as tensões de linha têm o mesmo módulo:
Você também pode conferir esse conteúdo em vídeo:
Passo 4: Calcular os Ângulos da Tensão de Linha
Falta calcularmos os ângulos dessas tensões de linha. Como a sequência é abc, as tensões de linha estão adiantadas em relação às tensões de fase em
Circuito Trifásico: Conexão Estrela-Triângulo (Y-Δ)
O sistema estrela-triângulo equilibrado é formado por uma fonte trifásica em estrela equilibrada ligada com uma carga em triângulo também equilibrada, como no exemplo abaixo:
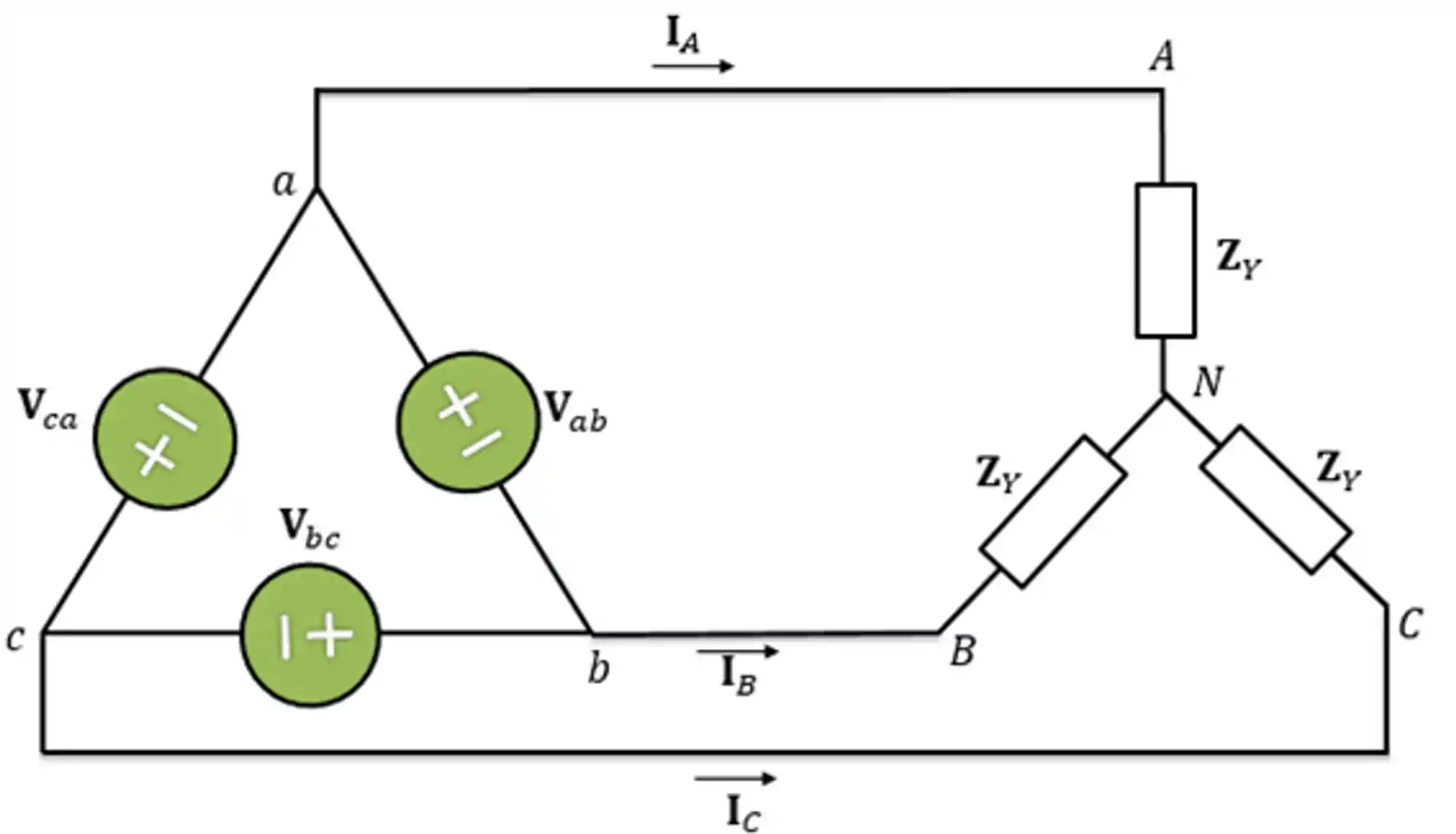
Circuito Trifásico: Conexão Triângulo-Triângulo (Δ-Δ)
A conexão triângulo-triângulo pode ser representada da seguinte forma:
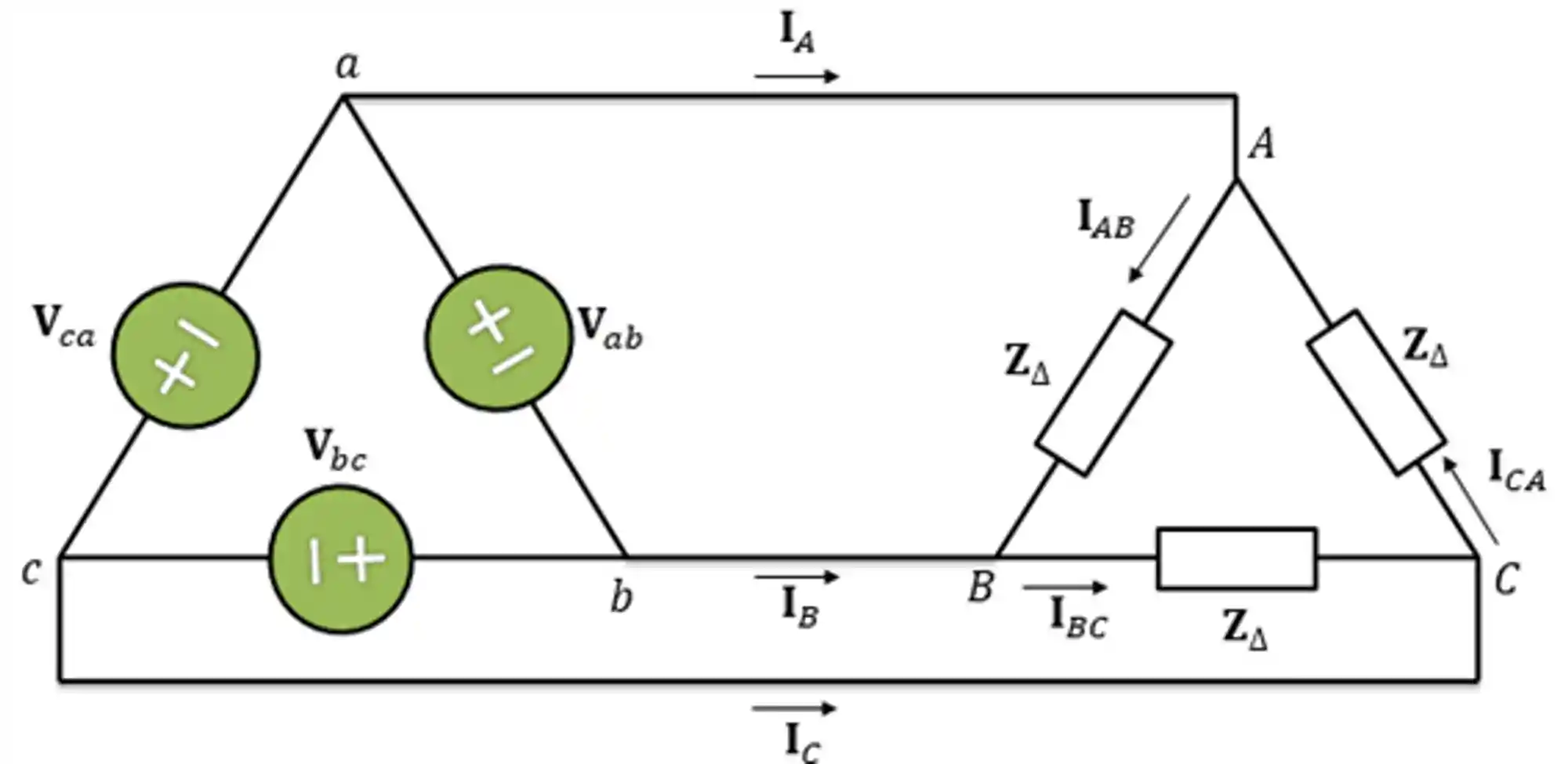
O triângulo-triângulo equilibrado é formado por uma fonte trifásica em triângulo equilibrada ligada com uma carga em triângulo também equilibrada e sua análise é praticamente a mesma dos casos anteriores.
Circuito Trifásico: Conexão Triângulo-Estrela (Δ-Y)
Para a conexão do tipo triângulo-estrela temos:
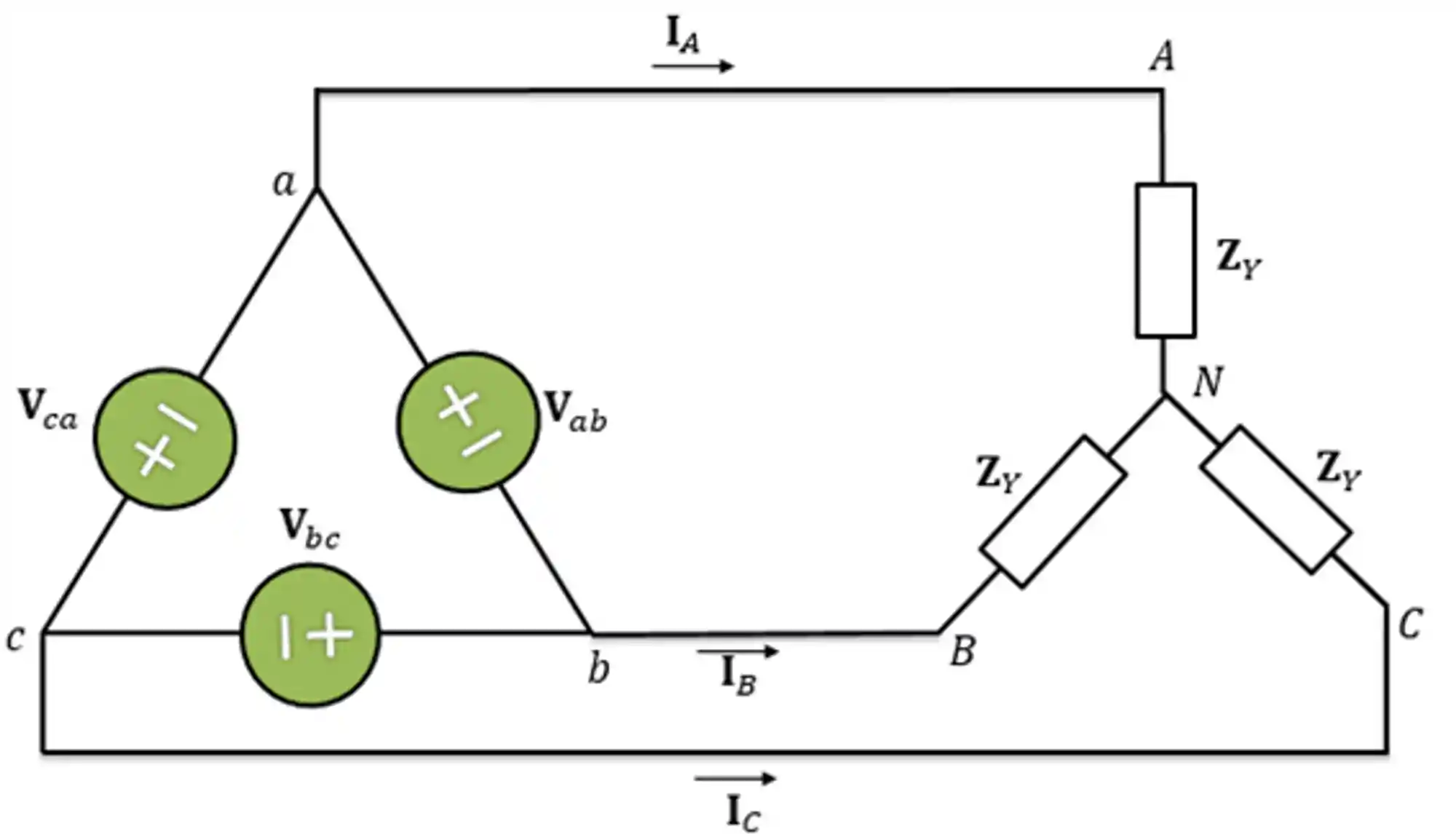
Como podemos ver, o sistema ∆-Y equilibrado é formado por uma fonte trifásica em triângulo equilibrada ligada com uma carga em estrela também equilibrada. Normalmente, quando temos esse circuito, nós transformamos a fonte de triângulo para estrela através das relações entre as tensões de linha e de fase.
Potência Trifásica
A potência instantânea em um circuito trifásico é dada pela soma da potência instantânea de cada fase:
Onde as tensões da fase são:
As correntes de fase são:
Sendo
Olha que interessante! A potência no circuito trifásico, seja ele qual for, é uma constante. Ou seja: ela não varia com o tempo como ocorre com as potências de apenas uma fase. Com isso, a potência instantânea é igual a potência média
Agora vamos praticar com exercícios?