Seja Q uma matriz ortogonal
(a) Considere a matriz onde
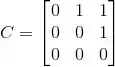
Determine explicitamente
(b) Determine os autovalores da matriz onde
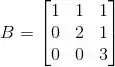
Passo 1
(a) Sabemos que:
E é a matriz multiplicada por ela mesma 501 vezes!!!!
Pra questão ter pedido algo desse tipo, é porque com certeza vai aparecer algum padrão enquanto fazemos essas multiplicações, então não se assustem!
Vamos começar a multiplicar C por ela mesma:
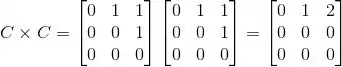

Ou seja, a partir de agora, sempre que multiplicarmos por C de novo vamos obter a matriz nula.
Então:
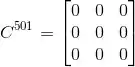
E:
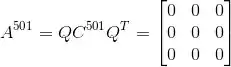
Passo 2
(b) Vamos dizer que:
Lembra que o enunciado disse que Q é ortogonal??
Isso significa que:
Então:
Por isso, pela definição, a matriz A é semelhante a matriz B.
E duas matrizes semelhantes tem os mesmos autovalores.
Logo, achar os autovalores de é a mesma coisa que achar os autovalores de B.
Como temos a matriz B, vamos calcular os autovalores dela.
Fazendo que:
Ficamos com:
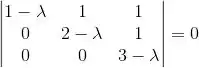
E achamos os autovalores:
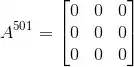
Resposta
(a)
(b) , e