Uma barra rígida de comprimento e peso é mantida a apoiada em uma escora de comprimento . A escora é posicionada de modo a receber a menor força de compressão possível. Desprezar o peso da escora e supor que , e funcionem como apoios simples. Calcular:
o ângulo para o qual a força na escora é mínima;
a força mínima;
a área da seção transversal da escora, sendo a tensão admissível do material da mesma;
o encurtamento da escora;
a energia de deformação acumulada.
Dica do Expert: Em um momento desse exercício, pode ser útil lembrar que e que . (Essas duas fórmulas vêm das fórmulas para seno e cosseno de .)
Passo 1
O que está acontecendo?
O momento gerado pelo peso da barra rígida é equilibrado pelo momento gerado pela força que a escora faz na barra:
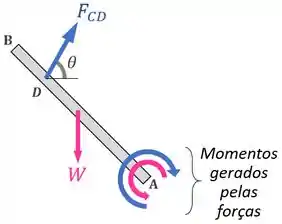
Daí que, pelo princípio da ação e reação, a barra vai reagir à força feita nela pela escora com uma força de compressão na escora de mesma intensidade :
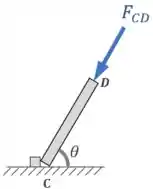
E o que é que o exercício quer?
Nos itens e , o exercício quer que a gente analise essa força , para que depois, a gente use ela para calcular outros valores nos itens , e .
Daí que o grande desafio desse exercício é encontrar uma expressão para a força .
Para fazer isso, vamos ter que aplicar as condições de equilíbrio na barra , o que vai nos dar um tanto de trabalho uma vez que o braço e a direção de dependem do ângulo .
Depois que tivermos uma expressão para , vamos poder prosseguir, item por item, fornecendo as respostas do exercício!
Passo 2
Então, vamos começar aplicando as condições de equilíbrio na barra !
Fazendo um diagrama de corpo livre dela, temos as seguintes forças:
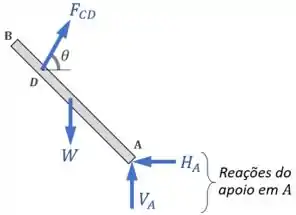
A condição de equilíbrio que vai nos permitir encontrar uma expressão para a força mais facilmente vai ser o equilíbrio de momentos em relação ao ponto :
Agora, calcular o momento da força inclinada é um tanto complicado, então vamos decompor ela em uma componente horizontal e uma componente vertical :
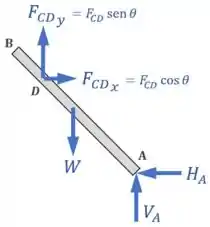
Em seguida, antes de podemos fazer o somatório de momentos , precisamos encontrar os braços das forças , e em relação ao ponto .
Então, vamos fazer uma pausa para olhar para os ângulos do exercício e encontrar os braços das forças!
O peso atua no meio da barra rígida de comprimento , mas a barra está com uma inclinação de , então temos que o braço do peso vai ser igual à , como mostra a figura:
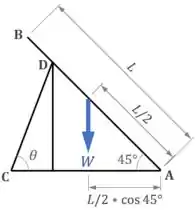
Já o braço da força vai ser igual à , como mostra a figura abaixo:
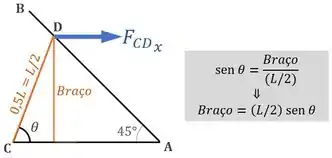
Por fim, o braço da força vai ser igual ao braço da força :
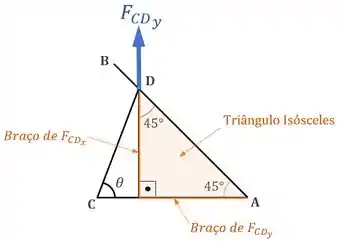
Passo 3
Agora que entendemos como são os braços das forças em relação ao ponto , podemos finalmente realizar o somatório de momentos:
As forças e vão realizar um momento no sentido anti-horário (), enquanto que a força vai realizar um momento no sentido horário ().
Dessa forma, o somatório de momentos fica assim:
Substituindo os valores encontrados para os braços, temos que:
Dividindo tudo por , isso fica assim:
Passando a parte que está subtraindo para o outro lado e depois substituindo e , encontramos que:
E, finalmente, isolando , encontramos uma expressão que descreve essa força:
Passo 4
Pronto! Agora que temos uma expressão que descreve a força , podemos passar a resolver os itens do exercício.
Começando pelo item : Calcular o ângulo para o qual a força na escora é mínima.
Bom, a força é dada por:
Essa expressão vai ser mínima quando a expressão “” que está dividindo ela for máxima.
Agora, se a gente se lembrar lá de cálculo, vamos nos lembrar que os máximos e mínimos das funções ocorrem quando as suas derivadas são iguais à zero.
Então vamos aplicar essa condição da derivada igual a zero aqui e descobrir qual é o valor de que satisfaz ela:
Usando a regra do produto , isso fica assim:
Lembrando que derivada de seno é cosseno e que derivada de cosseno é menos seno, conseguimos calcular essas derivadas:
E fazendo as multiplicações e arrumando tudo, isso fica assim:
Agora, eu não vou mentir: fiquei chateado/perdido com esse exercício quando cheguei aqui.
A gente quer isolar para descobrir o valor de que satisfaz a condição da derivada igual à zero, mas nessa expressão acima, não tem nenhum jeito fácil de isolar .

Aí eu fui dormir....
No dia seguinte, quando acordei, percebi que aquela expressão acima me lembrava das fórmulas do seno e cosseno de :
E pois não é que quando você usa que e , você encontra que:
Daí que, usando isso, você pode pegar a expressão que tinhamos encontrado:
E reescrever ela assim:
Passando pro outro lado, temos que:
Dividindo tudo por , isso fica assim:
E enquanto que o primeiro ângulo a ter uma tangente igual a é o ângulo de , o primeiro ângulo a ter uma tangente igual a é o ângulo de , de tal forma que:
Sendo assim, encontramos o ângulo para o qual a força vai ser mínima!
Felizmente, à partir daqui, o exercício fica mais tranquilo. 😊
Passo 5
Item resolvido, seguimos para o item : Calcular a força mínima.
Pegando a expressão que tinhamos encontrado para a força , temos que:
Como acabamos de ver que é mínima quando , a força mínima vai ser:
A gente pode deixar esse resultado em função dos senos e cossenos assim.
Ou a gente pode usar uma calculadora para encontrar o que todos esses senos e cossenos vão dar.
Usando a calculadora, encontramos que:
Passo 6
No próximo item, o item , queremos calcular a área da seção transversal da escora, sendo a tensão admissível do material da mesma.
Então vamos nos lembrar...
Se um material tem uma tensão admissível , isso significa que a tensão no material tem que ser menor ou igual que essa tensão admissível:
E a tensão normal na nossa escora pode ser dada pela fórmula da tensão normal média:
Agora, nós vimos lá no primeiro passo, quando entedemos o que estava acontecendo no exercício, que a escora está submetida a uma força de compressão .
Então a intensidade da força interna normal na nossa escora vai ser igual à intensidade dessa força , que calculamos como .
Fazendo essa substituição, a expressão anterior fica assim:
Isolando a área , que é o que queremos encontrar, obtemos que:
Ou seja, a área mínima da seção transversal da escora vai ser:
E assim finalizamos o item .
Passo 7
Para o item , queremos calcular o encurtamento da escora.
Esse encurtamento também pode ser entendido como a variação de comprimento que a escora sofre quando é comprimida e que é dada pela fórmula:
Sabemos que a escora possui uma força interna normal , e um comprimento .
E podemos considerar que ela possui um módulo de elasticidade e uma área igual a área mínima que ele pode ter, que foi encontrada no último item.
Fazendo isso, temos que:
Cortando em cima e em baixo e arrumando essa equação, ela fica assim:
Ou seja, o encurtamento na escora é:
Passo 8
Finalmente (!), chegamos ao item : Calcular a energia de deformação acumulada na escoa.
Se considerarmos que o material da escora está se comportando de forma linear-elástica/de acordo com a Lei de Hooke, vamos ter que a energia de deformação na escora vai ser dada por:
Onde:
- é a tensão na escora. Se considerarmos que a escora possui a menor área de seção transversal possível, vai ser igual a ;
- é a deformação na escora, que pode ser calculada pela Lei de Hooke . Considerando uma tensão , vamos ter que ;
- E é o volume da escora.
Fazendo essas considerações, a energia de deformação fica assim:
Arrumando, isso dá:
E, assim, finalizamos o exercício!