A estrutura abaixo suporta um peso em sua ponta e é sustentada pelo cabo de aço , que forma um ângulo com a horizontal. Considerando que o cabo de aço possuí uma área de seção transversal e que ele se comporta de acordo com a Lei de Hooke, possuindo um módulo de elasticidade , determine:
a força de tração no cabo em função do ângulo ;
o valor de para o qual a força é mínima;
& a densidade de energia de deformação no cabo quando é mínima.
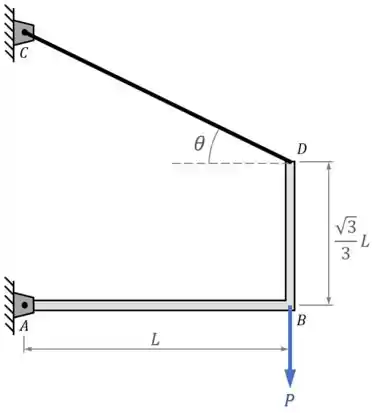
Passo 1
O que está acontecendo?
A estrutura traciona o cabo de aço com uma força .
O cabo reage a essa tração fazendo uma força de mesma intensidade que contribui para o equilíbrio da estrutura, como mostra o Diagrama de Corpo Livre da estrutura:
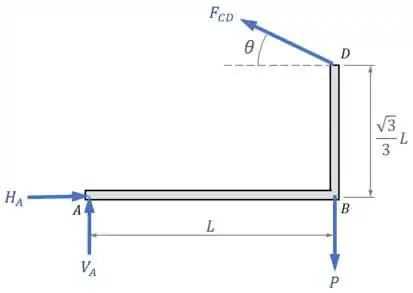
Aplicando as condições de equilíbrio nessa estrutura , é possível encontrar uma expressão para a força em função do peso e do ângulo , respondendo assim o item .
Em seguida, para responder o item , vamos ter que usar a propriedade que vimos em cálculo que diz que os máximos e mínimos de uma função ocorrem quando a sua derivada é igual a zero.
Por fim, para resolver o item , vamos ter que utilizar o valor encontrado para no item anterior para encontrar a força mínima.
Com isso, vamos poder calcular a tensão normal média no cabo de aço, e, em seguida, calcular a densidade de energia de deformação .
Passo 2
Começando pelo item :
Para encontrar a força em função do ângulo , vamos ter que observar o Diagrama de Corpo Livre da estrutura :
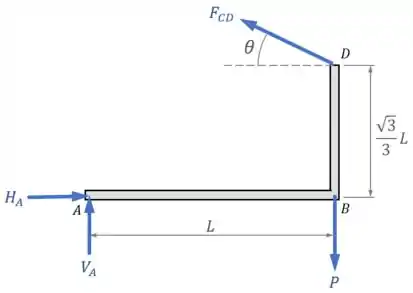
E aplicar as condições de equilíbrio para essa estrutura.
Então vamos pensar...
A condição de equilíbrio que nos permite encontrar sem que a gente tenha que se preocupar em calcular as reações no apoio em ( e ) vai ser o equilíbrio de momentos em relação ao ponto :
Em relação ao ponto , já conseguimos ver que o peso vai gerar um momento no sentido horário () com um braço .
Quanto a força , fica difícil visualizar o braço do momento que ela vai gerar uma vez que ela é uma força inclinada.
Para facilitar nossa vida, podemos decompor em uma componente horizontal e uma componente vertical :
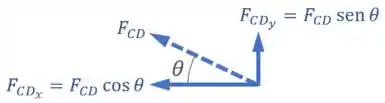
Pensando assim, vamos ter que, em relação ao ponto :
- A força vai gerar um momento no sentido anti-horário () com um braço ;
- E a força vai gerar outro momento no sentido anti-horário (), mas com um braço .
Agora que entendemos como vão ficar os momentos em relação ao ponto , podemos fazer o somatório de momentos, que fica assim:
Dividindo tudo por e passando para o outro lado, temos que:
Substituindo e :
Tirando em evidência:
Finalmente, isolando encontramos que:
E assim está resolvido o item !
Passo 3
Agora, no item , temos que analisar para qual valor de a força abaixo vai ser mínima:
Bom, essa força vai ser mínima quando a expressão “” que está dividindo ela for máxima.
Agora, lá em cálculo nós vimos que os máximos e mínimos das funções ocorrem quando as suas derivadas são iguais à zero.
Então vamos aplicar essa condição da derivada igual a zero aqui e descobrir qual é o valor de que satisfaz ela:
Sabendo que derivada de seno é cosseno e que derivada de cosseno é menos seno, essa derivada fica assim:
Passando para o outro lado, temos que:
Dividindo tudo por , encontramos que:
O que significa que:
O ângulo que possui tangente igual à é o ângulo de , então temos que:
Ou seja, podemos dizer que a força é mínima quando !
Passo 4
Finalmente, para o item , vamos precisar da tensão normal média no cabo de aço para podermos encontrar a densidade de energia de deformação .
Para encontrar , vamos primeiro encontrar o valor da força mínima, e, em seguida, encontrar a tensão normal média correspondente.
Aplicando a fórmula que encontramos para no item , temos que:
Substituindo :
Como e :
Simplificando essa expressão, ela fica assim:
Ou seja:
Simplificando mais uma vez, finalmente encontramos que:
Ou seja, a força mínima no cabo de aço ocorre quando e é igual a .
Além disso, como a força é a força de tração no cabo, vamos ter que a força interna normal no cabo vai ser igual a , ou seja:
E essa força normal vai gerar uma tensão normal média no cabo de aço:
Passo 5
Agora que conhecemos o valor da tensão normal média no cabo quando a força é mínima, podemos calcular a densidade de energia de deformação no cabo nesse caso.
Da fórmula da densidade de energia de deformação , temos que:
Nós não conhecemos a deformação no cabo, mas sabemos que o cabo está seguindo a Lei de Hooke , de tal forma que:
Fazendo essa substituição na fórmula de , encontramos que:
Substituindo o valor encontrado para a tensão normal média :
O que nos dá a resposta para o item :