Os dados obtidos em um ensaio de tensão-deformação para um material cerâmico são dados na tabela. A curva é linear entre a origem e o primeiro ponto. Represente o diagrama em gráfico e determine o valor aproximado do módulo de tenacidade. A tensão de ruptura é .
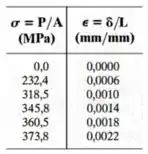
Dica do Expert: Se você fez o exercício passado, o gráfico é o mesmo!
Passo 1
O primeiro passo desse exercício é desenhar o gráfico, que vai ser o mesmo do exercício passado, caso você já tenha feito ele:
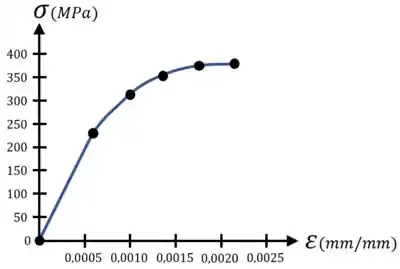
Passo 2
Agora, em seguida, o exercício quer que a gente calcule o módulo de tenacidade do material.
Lembra aí!
Para calcular isso, vamos ter que calcular a área debaixo de todo o gráfico do diagrama tensão-deformação desse material:
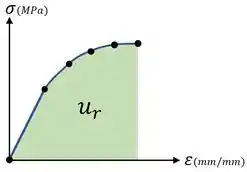
E, para calcular essa área, vamos ter que aproximar ela como a soma das áreas de uma série de triângulos, retângulos e trapézios que aproximam essa curva.
A gente pode escolher dividir essa área como quiser! Só devemos evitar ignorar algum pedaço grande de área.
Para obter o mesmo gabarito do livro, dividimos essa área assim:
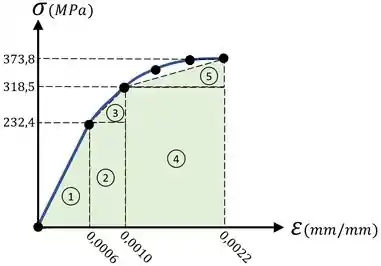
De tal forma que vai ser a soma das áreas das regiões a :
Observando o gráfico, calculamos essas áreas individuais assim:
Finalmente, calculando tudo isso, encontramos que:
Resposta
(O seu resultado pode ser maior ou menor, já que o cálculo de é aproximado.)