Um atleta ao fazer exercício de flexão no solo para em equilíbrio estático na posição superior, desenhada abaixo. Seu corpo guarda um ângulo com a horizontal. Considere o corpo como uma barra fina, homogênea de massa , apoiada em um ponto O localizado no ponto de contato da extremidade dos pés com o solo. Admita o centro de massa (CM) distante do eixo de rotação. Considere os braços na vertical, de massa desprezível, fazendo uma força total vertical sobre um ponto B nos ombros. O ponto B dista do eixo de rotação O. A aceleração da gravidade é .
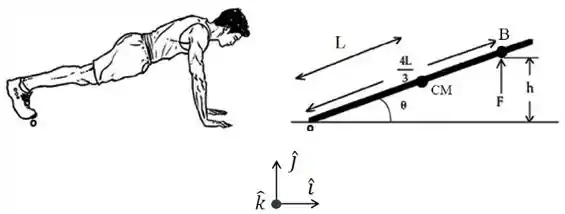
(a) Encontre uma expressão literal para o valor da força aplicada em B em função dos dados fornecidos.
(b) Obtenha uma expressão literal para o módulo da força normal que o solo produz sobre os pés do atleta em função dos dados fornecidos.
Passo 1
Temos que a “barra” está em equilíbrio estático. Isso significa que ela está em repouso tanto para translação quanto para rotação.
Então, tanto o somatório de forças tem que ser zero:
Quanto o somatório de torques tem que ser zero:
Beleza, isso é um bom ponto de partida.
Passo 2
Na letra (a), queremos achar o valor da força .
Quais são as forças sobre a barra?
Lembrando que a força peso está aplicada no CM e a força normal é perpendicular à superfície:
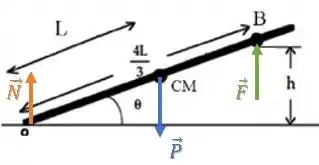
Podemos pensar em usar qualquer uma daquelas duas equações de equilíbrio...
Dá um olhada na equação do somatório de forças:
Nós já conhecemos a força peso da barra, pois temos a massa e a gravidade .
Porém, não conhecemos nem a força , que queremos, nem a força normal . Assim, não conseguimos resolver o problema só com isso.
Passo 3
Temos que usar a equação do somatório de torques:
Teoricamente, poderíamos calcular o torque em qualquer ponto da barra, já que em todos ele é nulo.
Mas, vamos calcular o torque das forças a partir do ponto de rotação O, pois assim, o torque da força normal será nulo, já que a força está aplicada no eixo de rotação .
Assim, teremos apenas o valor da força como desconhecido:
Passo 4
Vamos ao cálculo dos torques e .
Torque é calculado como o produto vetorial entre o vetor distância e o vetor força :
Para a nossa barra, esses vetores ficariam assim, para a força peso, por exemplo:
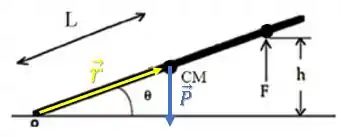
Para calcular o módulo desse torque, podemos optar por duas opções, que resultam NO MESMO VALOR:
Opção 1: Decompor a força peso em suas componentes paralela e perpendicular ao vetor .
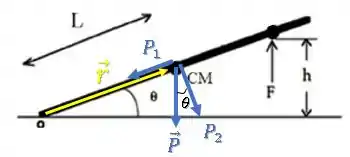
Como apenas a componente perpendicular ao raio gera torque, teríamos:
Opção 2: Decompor o vetor nas componentes paralela e perpendicular à foça peso .
Como a força peso apenas gera torque perpendicularmente ao raio, só precisamos fazer isso:
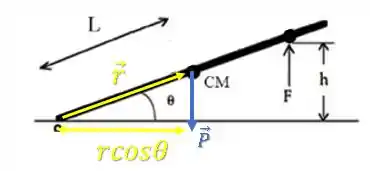
Então o torque da força peso fica assim:
OBS: Se você está confuso em porque apareceu um cosseno do ângulo em vez de um seno como naquela fórmula de produto vetorial:
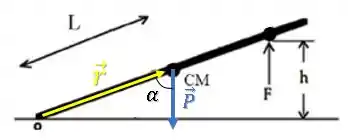
Essa fórmula funciona para o ângulo entre os dois vetores e .
No caso da barra, o ângulo entre os dois vetores seria esse ângulo aqui:
Enfim, voltando...
Passo 5
Vamos usar a opção 2.
Então, já vimos que o torque da força peso é:
A distância é:
Então:
Vamos fazer o mesmo procedimento para a força .
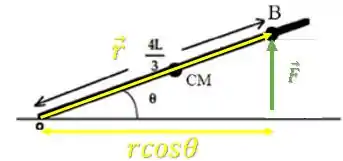
O torque da força será:
O valor de é:
Então:
Passo 6
Vamos voltar à equação dos torques e encontrar o valor de .
Devemos tomar muito cuidade com o sinal de cada torque!
Olha aqui para as forças:
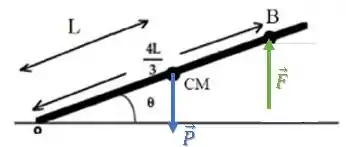
A força peso tenta girar a barra no sentido horário enquanto a força tenta girar a barra no sentido anti-horário.
Então, seus torques devem ter sinais opostos:
Cortando e , temos:
Substituindo :
Achamos o valor da força para a letra (a).
Passo 7
Na letra (b), queremos o valor da força .
Agora que já tivemos esse trabalho todo para achar essa força , achar a força normal fica fácil.
Poderíamos calcular o torque com relação a um ponto diferente, o que dá um pouco de trabalho...
Ou então, usar aquela primeira equação de equilíbrio de forças:
Substituindo os valores das forças, temos:
Ufa, essa foi mole!

Resposta
(a)
(b)