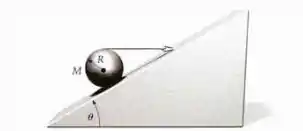
Uma esfera homogênea, de raio e massa , é mantida em repouso, por um cordão horizontal, sobre um plano inclinado de ângulo , como mostrado na figura abaixo. Seja .
- Qual é a tração no cordão?
- Qual é a força normal exercida sobre a esfera pelo plano inclinado?
- Qual é a força de atrito atuando sobre a esfera?
Passo 1
Primeiro, vamos marcar as forças que atuam na figura.
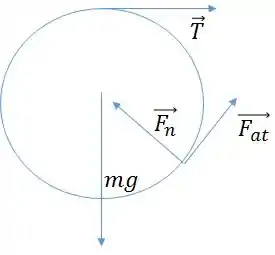
: Força normal, perpendicular à superfície
: Tração da corda
: Força de atrito
: Força peso
Conforme mostra a figura abaixo:
Passo 2
Vamos agora analisar as equações de equilíbrio. Mas antes disso, vamos mudar o eixo para a seguinte forma:
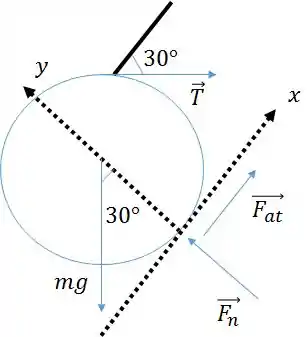
Por que isso?
Nossa análise vai ficar mais simples.
Já temos o ângulo de inclinação das forças e e podemos achar a decomposição desses vetores facilmente utilizando o ângulo ( lembre-se de cosseno é o lado colado ao ângulo e seno o lado oposto).
Passo 3
Agora que montamos o diagrama de forças, podemos aplicar as condições de equilíbrio.
Vamos começar aplicando para um eixo de rotação no centro da esfera. Dessa forma, sabemos que os momentos gerados por e são zeros.
Perceba que a distância do centro da esfera (eixo de rotação) até a linha de atuação das forças e vale . Essa distância também é perpendicular à linha de ação das duas forças. Assim, podemos aplicar, escolhendo o sentido anti-horário como positivo:
Passo 4
Vamos agora aplicar as outras condições de equilíbrio estático. Mas, antes disso, vamos decompor as forças necessárias.
Lembrando que mudamos os eixos tradicionais lá em cima para a análise ficar mais simples.
Sendo assim, está no eixo e no eixo e precisamos achar as componentes das forças e .
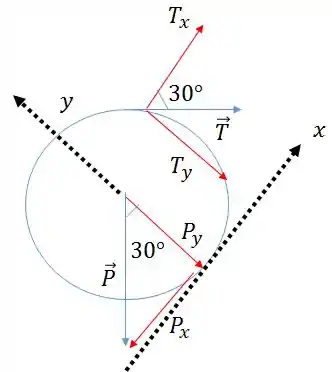
Agora ficou mais tranquilo fazer essa decomposição:
Passo 5
Agora podemos aplicar as outras condições de equilíbrio estático.
Vamos começar por para descobrirmos .
Como :
Passo 6
Vamos aplicar agora para descobrirmos .
Passo 7
Pela equação de momento que aplicamos no passo 3, sabemos que: