Na figura abaixo, uma esfera uniforme de massa e raio é mantida em repouso por uma corda de massa desprezível, presa a uma parede sem atrito a uma distância acima do centro da esfera.
Determine
- A tensão da corda
- A força que a parede exerce sobre a esfera

Passo 1
Vamos montar o problema.
Temos
a força normal
o peso da bola
a tração
o ângulo que a tração faz com a parede
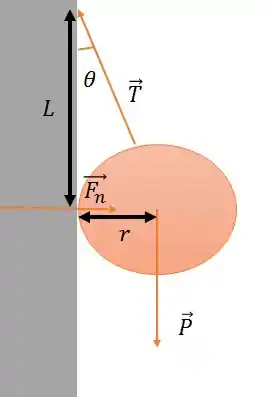
Passo 2
Podemos descobrir o valor desse ângulo, já que temos os dois catetos de um triângulo retângulo e r.
Passo 3
Então, podemos aplicar as condições de equilíbrio.
Vamos aplicar
Para isso, temos que decompor em e .
Pela figura, aplicando decomposição de vetores, vemos que
, repare que o sentido está negativo
Então,
Passo 4
Vamos resolver as equação.
Vou começar pela
Passo 5
Agora aplcamos na equação: