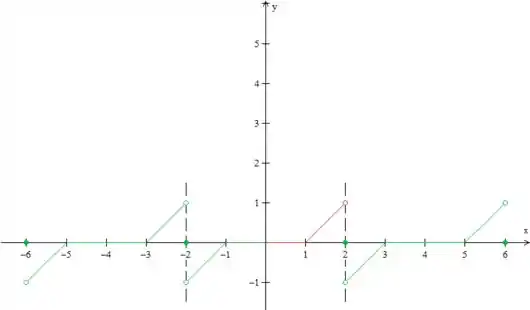
No problema é dada uma função em um intervalo de comprimento . Esboce os gráficos das extensões par e ímpar de de período .
Passo 1
Vamos começar pela extensão par, que é mais simples. A primeira coisa que você deve fazer é desenhar os dados do problema (que estão entre colchetes):
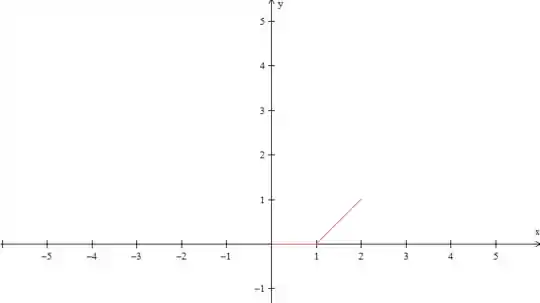
Certo. Agora, como queremos uma extensão par, vamos espelhar essa função no eixo , ok?
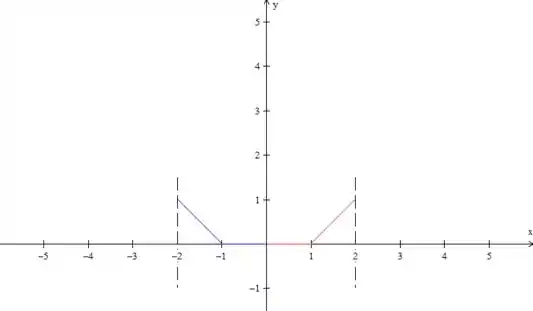
Beleza, esse vai ser o período da função, esse é o padrão que se repete, então vamos repetir isso para a esquerda e para a direita:
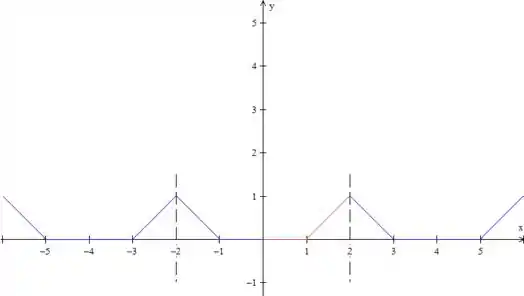
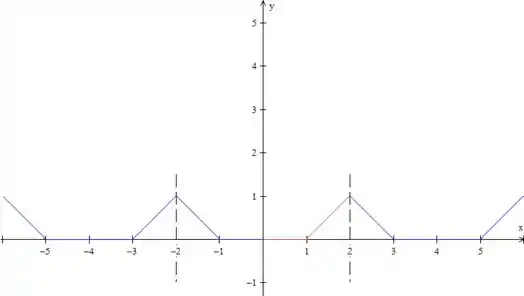
Pronto, essa é a extensão par de . É bom você sempre desenhar esse tracejado para marcar o período da função, para não se perder!
Passo 2
Agora queremos a extensão ímpar, ela é um pouco mais chatinha, mas a ideia é a mesma. Primeiro desenhamos o que o enunciado nos dá
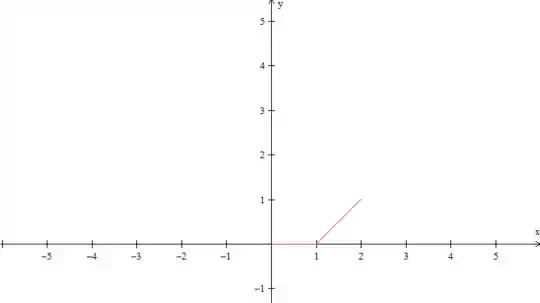
Agora rebatemos isso no eixo . Como assim? Isso não é a extensão par? Você já vai entender:
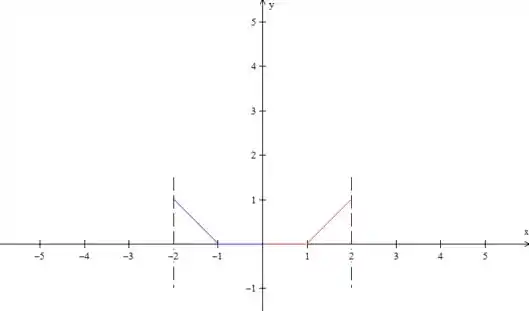
Agora, essa parte “nova” em azul, nós rebatemos no eixo , mas só ela! Em termos práticos: vamos jogar a função em azul para baixo:
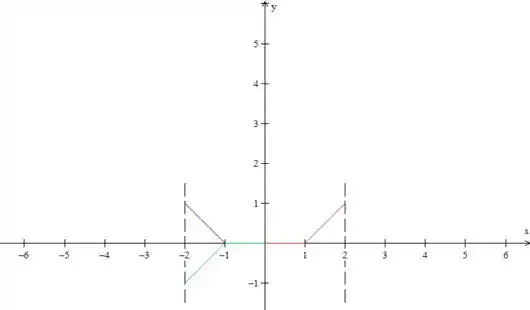
O padrão, que vai se repetir a cada período é então essa parte vermelha mais a verde. Vamos então “copiar” isso para a esquerda e para a direita, ok?
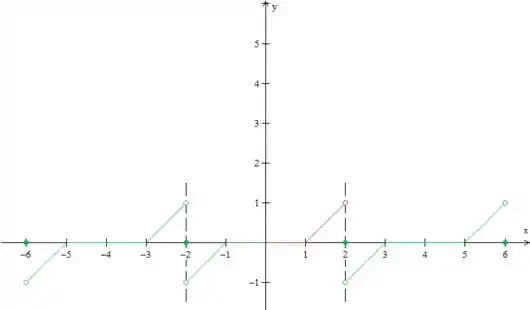
Repare que nós só definimos os pontos de descontinuidade no final. Por quê?
Para uma função periódica ser ímpar, devemos ter
Sempre! E foi o que nós fizemos aqui, por isso só escrevemos os pontos de descontinuidade no final (repare que todos os pontos preenchidos estão no ). Se essa condição não ocorrer, então a função periódica não satisfaz a simetria de uma função ímpar, lembre-se disso!
É interessante reparar também que uma função ímpar sempre vale zero na origem, pois é simétrica em relação a ela.
Resposta
a)
b)