Condução com Geração Térmica
Produzido por Giovanna RonzéTeoria
Introdução
Fala, galerinha! Tudo certo? Aqui nesse tópico a gente vai ver um caso especial de condução. É o caso em que energia térmica é gerada ou consumida dentro do corpo.
Mas você já parou pra pensar em como se gera ou se consome energia em um certo volume? Basicamente, a geração de energia térmica acontece em fios, chips e aquecedores, por onde uma corrente elétrica passa e acaba dissipando energia térmica por efeito Joule.
Mas pode ser também que esteja ocorrendo alguma reação exotérmica (libera calor) e a energia térmica esteja sendo gerada ali dentro. Por outro lado, se essa reação for endotérmica, uma parte da energia que entrar no volume pode ser consumida pela reação.

O que queremos fazer aqui é prever qual vai ser a temperatura em todos os pontos de uma geometria que esteja gerando ou consumindo calor. Pra isso, a gente precisa encontrar uma expressão que descreva a temperatura, ou seja, a distribuição de temperatura.
A gente já fez isso, tá lembrado? Agora, a diferença é que o termo de geração não será mais zero como estávamos considerando até aqui, então as coisas vão mudar um pouco!
Pra encontrar a distribuição de temperatura, a gente precisa recorrer à equação do calor e vocês vão perceber que a gente faz sempre o mesmo passo-a-passo:
- Identificar o sistema de coordenadas a ser usado (cartesiano, cilíndrico ou esférico);
- Fazer as simplificações que cabem ao problema;
- Integrar a equação na dimensão em que ocorre a condução ( ou );
- Agrupar de um lado da equação o termo da derivada e do outro o restante dos termos;
- Integrar a nova equação para obter o perfil de temperatura;
- Identificar as condições de contorno que podem ser usadas nas superfícies;
- Com as condições de contorno, calcular as constantes de integração;
- Xablau! Teremos a distribuição de temperatura no corpo.
Bora ver se isso dá certo mesmo? Se liga aí então!
Parede Plana
Bora encontrar o perfil de temperaturas nas paredes nas situações onde há geração de calor dentro delas.
Passo 1: Como o sistema é retangular, a gente vai usar a equação do calor em coordenadas cartesianas:
Passo 2: Hipóteses simplificadoras:
- Condução unidimensional em : não há variação em ou .
- Estado estacionário: não há variação ao longo do tempo.
- Com geração de energia: o termo é diferente de zero.
- Propriedades constantes: a condutividade térmica pode sair da derivada.
Assim, a Equação do Calor fica dessa forma:
Passos 3 e 4: Assim, podemos fazer a primeira integração da equação em relação a :
Passo 5: Integrando mais uma vez a equação em termos de :
Prontinho! Esse será o perfil de temperaturas em uma parede plana com geração:
Os Passos 6 e 7 dependem das condições de contorno que o problema der. E aí, Xablau!
Pela equação, com aquele lá, a gente vê que a temperatura se comporta como uma parábola ao longo de . Basicamente, uma parábola pode ter sua concavidade pra cima ou pra baixo, certo? O que vai dizer isso é o termo que multiplica !
- Se o calor for gerado dentro da parede, então . Dessa maneira, o termo que multiplica é negativo e a parábola tem concavidade pra baixo.
- Se o calor for consumido dentro da parede, então . Dessa maneira, o termo que multiplica é positivo e a parábola tem concavidade pra cima.
Mas mesmo quando definida a concavidade da parábola, as condições de contorno podem mexer com a cara da curva, dá uma olhada:
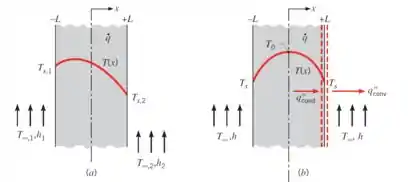
A imagem mostra o caso em que a condição de contorno de um lado é diferente da do outro lado. Já a imagem mostra o caso em que as duas condições de contorno são iguais (simetria).
Sistemas Cilíndricos
Como eu te disse no passo-a-passo, a única coisa que muda para sistemas cilíndricos é que trabalhamos com coordenadas diferentes: as coordenadas cilíndricas. Lembra da Equação do Calor em coordenas cilíndricas? Não? Então tá aí:
Admitindo a condução unidimensional em e todas as outras considerações lá de cima, a gente fica com o seguinte:
Integrando a equação em termos de :
Assim:
Integrando novamente a equação em termos de , a gente fica com:
Mesmo esquema, viu? Esse é o perfil de temperatura em cilindros e cascas cilíndricas (anéis). Pra descobrir as constantes, é só a gente aplicar as condições de contorno do problema.
Sistemas Esféricos
Tá cansado já de ver a mesma coisa, não? Então vou agilizar as coisas pra você, já que a gente é parça! Se a gente não lembrava da equação com coordenadas cilíndricas, a da esfera então... Então, olha só:
Com aquelas simplificações todas, só resta isso aqui:
E depois de aplicar o nosso passo-a-passo maroto, a gente consegue o perfil de temperatura numa esfera:
E, mais uma vez, as constantes saem das condições de contorno que você aplicar!
Agora que vocês já estão craques com as equações de calor, bora dar uma exercitada. Então se alonga aí e parte pras questões!
Parede Plana
Sistemas Cilíndricos
Sistemas Esféricos
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma parede plana é composta por dois materiais e. A parede de material apresenta uma geração de energia de , e espessura de . A parede de material , sem geração de calor, é caracterizada por e .
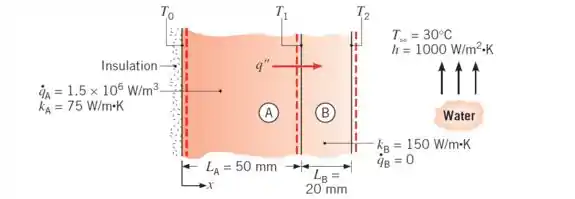
A superfície interna do material é bem isolada, enquanto que a superfície externa está sendo resfriada por uma corrente de água a e .
Esquematize o perfil de temperatura que existe no sistema sob condições de estado estacionário.
Determine a temperatura da interface dos materiais e a temperatura da superfície resfriada.
Passo 1
Esquematize o perfil de temperatura que existe no sistema sob condições de estado estacionário.
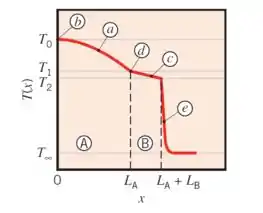
Já discutimos nos tópicos anteriores como são os perfis de temperatura na parede plana com geração (parabólico) e sem geração (reta). Então vamos analisar como o perfil de temperatura se comporta em cada material.
Material A:
Além disso, sabemos que o fluxo de calor na superfície isolada é zero, ou seja:
Se a derivada da temperatura é nula, isso significa que esse ponto será um ponto de máxima ou de mínima temperatura.
Como há geração de calor na superfície A e esse calor só escapa pela direita (lado do material B), podemos afirmar que:
Sendo assim, a gente conclui que a temperatura em é um ponto de máximo e a parábola no material tem concavidade pra baixo!
Passo 2
Material B:
Por fim, a gente pode avaliar a derivada das curvas na transição do material A para o material . “Mas como?”
A condutividade térmica nos dá essa informação! Quanto maior a condutividade térmica de um material, menor será a resistência térmica de condução e, consequentemente, as temperaturas estre duas extremidades serão mais parecidas.
Sendo assim, quando a gente avalia quantos graus variaram em um determinado espaço de tempo (conceito da derivada), esse valor será pequeno.
Sendo assim, como a condutividade térmica do material é maior que a do material , podemos afirmar que a derivada do perfil em será menor que a derivada em .
Passo 3
Por fim, o perfil de temperatura da superfície para o fluido é semelhante a uma exponencial, pois a convecção é um fenômeno muito intenso e a temperatura, em pouco espaço, já alcança o valor da temperatura no seio do fluido ().
Diante disso tudo, propomos o seguinte perfil de temperatura:
Passo 4
Determine a temperatura da interface dos materiais e a temperatura da superfície resfriada.
A temperatura da superfície externa () pode ser obtida se fizermos um balanço de energia na parede de material . Como não há geração nesse material, temos que o fluxo de calor que entra pela superfície a temperatura de é o mesmo fluxo que sai por convecção pela superfície a :
Esse fluxo de calor pode ser determinado por um segundo balanço de energia, mas agora na parede de material . Como não há fluxo pela superfícies isolada, todo o calor gerado no material , sai pela superfície em .
Dessa maneira, a gente pode escrever o seguinte:
Dividindo pela área de troca térmica, pra escrevermos em termos do fluxo de calor e não da taxa, ficamos com:
Igualando as duas expressões pro fluxo que achamos, teremos:
Isolando a temperatura , a gente fica com:
Onde:
Substituindo os valores:
Passo 5
Pra gente encontrar a temperatura , a gente pode fazer um circuito na parte da direita do sistema, porque ali não há geração então a gente pode montar circuito térmico!
Fazendo isso, teremos o seguinte:

Dessa maneira a gente pode escrever o fluxo de calor da seguinte forma:
Obs.: Estamso definindo as resistências térmicas associadas ao fluxo de calor, ao invés da taxa de transferência de calor.
Isolando a temperatura de interesse , a gente tem que:
Onde:
Substituindo os valores:
Resposta
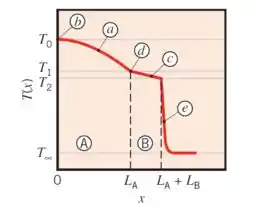
O perfil de temperatura no sistema é dado abaixo:
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
O ar no interior de uma câmara a é aquecido por convecção com por uma parede de espessura de e condutividade térmica com geração uniforme de calor de . Para evitar que a geração de calor no interior da parede seja perdida para o exterior da câmara a com , um aquecedor elétrico de fita é colocado na rede externa para fornecer um fluxo uniforme de calor .
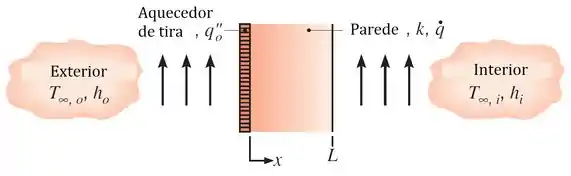
Esboce a distribuição de temperatura na parede em coordenadas para a condição em que não ocorre a perda do calor gerado no interior da parede para o exterior da câmara.
Quais são as temperaturas nas fronteiras da parede ( e ), para as condições do item ?
Determine o valor de que deve ser fornecido pelo aquecedor de fita de modo qe todo o calor gerado no interior da parede seja transferido para o interior da câmara.
Se a geração de calor da parede for interrompida e o fluxo de calor do aquecedor de fita mantido constante, qual seria a temperatura em regime estacionário da superfície externa da parede?
Passo 1
Esboce a distribuição de temperatura na parede em coordenadas para a condição em que não ocorre a perda do calor gerado no interior da parede para o exterior da câmara.
Nosso objetivo aqui é construir o perfil de temperatura dentro da parede com geração. Para isso, temos que recorrer à equação do calor em sistemas cartesianos:
Ao admitir a condução somente na direção e propriedades constantes, avaliando o estado estacionário, ficamos com:
Reorganizando a equação:
Assim, podemos integrar a equação em relação a :
Integrando mais uma vez a equação em termos de :
Assim, temos que o perfil de temperaturas é dado por:
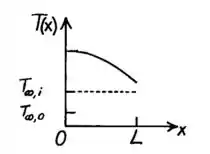
Logo, verificamos que o perfil de temperatura é parabólico! Para saber exatamente como ele é, a gente precisa das condições de contorno! Mas de forma qualitativa, a gente pode avaliar o seguinte:
A função é um semi-parábola, porque em não há perdas de energia para o ambiente, porque um fluxo de calor é fornecido nesse ponto de mesmo valor que seria a perda de energia por convecção.
Concluímos que a derivada da temperatura é zero em e, consequentemente, esse é um ponto de máximo ou de mínimo.
Como um fluxo de calor é fornecido na superfície em , espera-se que essa superfície seja mais quente que a de , logo é um ponto de máximo!
Então, o perfil será:
Passo 2
Quais são as temperaturas nas fronteiras da parede e , para as condições do item ?
Temos agora que determinar quais as temperaturas da parede: e . Como já vimos na letra a), o perfil de temperaturas dentro da parede é dado por:
Então, se conseguirmos descobrir as constantes e , poderemos calcular a temperatura em qualquer posição de , inclusive nas extremidades como é o nosso objetivo!
Para isso, a gente precisa de condições de contorno! Vamos avaliar quais são as condições de contorno. O sistema é o seguinte:
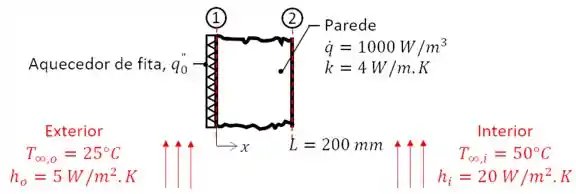
Note que, na superfície , temos a condição de um fluxo zero () e, na superfície , temos a condição do fluxo de condução ser igual ao de convecção. Então vamos trabalhar com cada condição separadamente.
Passo 3
Condição de contorno 1: fluxo zero na parede.
Já sabemos a expressão para a derivada da temperatura na letra a):
Em , temos:
Substituindo na equação:
Passo 4
Condição de contorno 2: fluxo de condução igual ao de convecção.
Substituindo a expressão da derivada da temperatura avaliada em , ficamos com:
Já sabemos que , então:
Logo:
Substituindo os valores:
Já achamos a temperatura de uma das extremidades só com essa condição de contorno! Show!
Passo 5
Se a gente avaliar o perfil em , ficaremos com:
Logo, concluímos que:
Avaliando o perfil de temperatura em , ficamos com:
Substituindo os valores:
Assim:
Passo 6
Determine o valor de que deve ser fornecido pelo aquecedor de fita de modo que todo o calor gerado no interior da parede seja transferido para o interior da câmara.
O aquecedor de tira deve fornecer um fluxo de calor suficiente para que a perda de calor para o exterior seja zero, ou seja, a quantidade de calor que ele fornece deve ser igual ao fluxo de calor que seria perdido por convecção:
Sendo assim, vamos calcular o calor de convecção que seria perdido se não houvesse o aquecedor:
Substituindo os valores:
Passo 7
Se a geração de calor da parede for interrompida e o fluxo de calor do aquecedor de fita mantido constante, qual seria a temperatura em regime estacionário da superfície externa da parede?
Se a geração de calor for interrompida a gente cai nas situações que já vimos nos outros tópicos: condução sem geração.
Sendo assim, a gente pode usar circuito térmico em todo o sistema! Dá uma olhadinha:
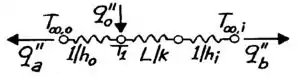
Fazendo um balanço de energia no nó de temperatura , a gente fica com:
Substituindo as expressões com as resistências térmicas:
Substituindo os valores de cada propriedade:
Reorganizando os termos, temos que:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um proprietário de um imóvel, cuja tubulação de água congelou durante um período de tempo frio, decide derreter o gelo passando uma corrente elétrica ao longo da parede do tubo. Os raios interno e externo são designados por e , e sua resistência elétrica por unidade de comprimento por . O tubo é bem isolado no exterior e durante a fusão do gelo (e água) permanece a uma temperatura constante no tubo associada ao processo de fusão.
Considerando que condições de regime estacionário são alcançadas logo depois da aplicação da corrente, determine a forma de distribuição de temperatura em regime estacionário na parede do tubo durante o processo de fusão.
Desenvolva uma expressão para o tempo necessário para fundir totalmente o gelo. Calcule esse tempo para , e .
Passo 1
Considerando que condições de regime estacionário são alcançadas logo depois da aplicação da corrente, determine a forma de distribuição de temperatura em regime estacionário na parede do tubo durante o processo de fusão.
Vamos antes de iniciar o problema, identificar todos os dados do enunciado: , , , , e . Beleza, então já sabemos que o perfil de temperatura solicitado deve estar em função somente desses parâmetros!
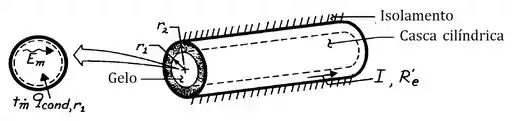
Como queremos determinar o perfil de temperatura em uma casca cilíndrica, vamos recorrer à equação do calor em coordenadas cilíndricas:
Ao admitir que a condução de calor é unidimensional em e as propriedades são constantes, temos que:
Pelo enunciado, as condições de regime estacionário são alcançadas instantaneamente, então, não há variação da temperatura ao longo do tempo. Assim:
Reorganizando a equação, a gente fica com:
Integrando a equação em termos de :
Reorganizando essa equação:
Integrando novamente a equação em termo de , a gente fica com:
Pronto! Esse é o perfil de temperatura num corpo cilíndrico. Mas repara que a gente não usou nenhum dos dados ainda! Isso porque a gente ainda não determinou as constantes e .
Passo 2
Pra gente determinar as constantes, precisamos das famosas condições de contorno. Pra identificar quais são as condições de contorno desse problema, dá uma olhadinha no esquema de novo aqui embaixo:
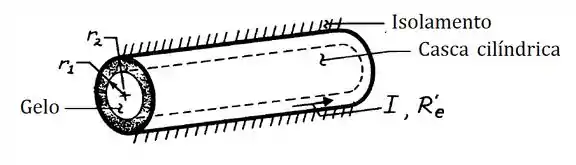
Pela imagem, a gente pode perceber que na superfície em , o fluxo de calor é zero, devido ao isolamento, então a condição de contorno será de fluxo constante nulo. Já em , a superfície está em contato com o gelo (), logo a condição de contorno será de temperatura constante e igual a .
Vamos trabalhar com uma condição por vez, beleza?
Passo 3
Bora usar essas condições de contorno agora:
- Condição de contorno 1: fluxo zero na parede em .
- Condição de contorno 2: temperatura constante e igual a .
Já encontramos no Passo 1, a expressão da derivada da temperatura:
Substituindo na equação:
Reorganizando a equação:
Passo 4
Substituindo na expressão do perfil que encontramos no Passo 1:
Então, ficamos com:
Avaliando em e substituindo o valor encontrado anteriormente de :
Passo 4
Pronto! Encontramos as duas constantes! Agora é só substituir na expressão do perfil de temperatura:
Reorganizando essa bagunça de letras, a gente fica com:
Esse é o perfil de temperatura na casca cilíndrica! Mas tem um detalhe: ele não tá escrito somente em termos daqueles parâmetros que mencionamos (, , , , e ). O calor gerado () não pode estar na expressão do perfil.
Passo 5
Pra solucionar esse problema, a gente vai tentar escrever ele em função dos demais parâmetros!
A gente sabe que a energia que é gerada é uma consequência do efeito Joule, ou seja, a corrente elétrica que passa dissipa uma taxa volumétrica de calor. E sabemos que a taxa de energia pode ser escrita como:
Assim:
Mas o dado é em termos de , ou seja, é a resistência por unidade de comprimento:
Em que é o comprimento da casca cilíndrica e é seu volume.
Em que essa área é a área transversal da casca cilíndrica:

Dessa maneira:
Substituindo as expressões:
Passo 6
Desenvolva uma expressão para o tempo necessário para fundir totalmente o gelo. Calcule esse tempo para , e .
Fazendo um balanço de energia no corpo de gelo, a gente fica com:
Dividindo pela unidade de comprimento , ficamos com:
Substituindo a expressão da taxa de calor volumétrica:
Com os valores do enunciado, temos que:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Considere uma embalagem de maçãs, cada uma com de diâmetro, na qual o ar escoa a e com velocidade de . O valor do coeficiente de transferência de calor por convecção é . No interior de cada maçã, a energia térmica é gerada uniformemente a uma taxa total de . A massa específica e a condutividade térmica da maçã são respectivamente e .
Determine as temperaturas do centro e da superfície da maçã.
Passo 1
Bora dar uma olhada num esquema que representa esse problema:
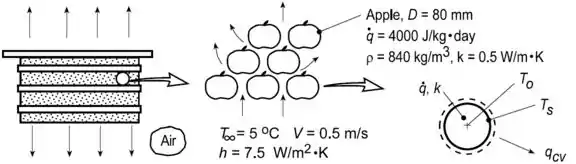
Como nosso objetivo é calcular a temperatura no centro e na superfície das maçãs e elas podem ser aproximadas de esferas, vamos usar a equação do calor em coordenadas esféricas:
Ao admitir que a condução é adimensional na direção e que as propriedades são constantes, considerando no regime estacionário, ficamos com:
Reorganizando a equação:
Integrando em termos do raio :
Reorganizando:
Integrando novamente:
Pronto! Conseguimos determinar o perfil de temperatura! Agora só a gente achar as constantes pelas condições de contorno.
Passo 2
Vamos avaliar a situação pra definir quais serão as condições de contorno:
A primeira condição de contorno que usaremos tem a ver com a simetria da esfera. “Como assim?”
Você pode pensar de duas formas diferentes:
- A energia que é gerada no volume da esfera acaba saindo por convecção pra todos os lados, devido à simetria do corpo. Sendo assim, o fluxo de calor no centro da esfera é zero.
- Como a energia é gerada em todo o volume e sai pelas superfícies, a gente pode esperar que o centro seja o ponto de máxima temperatura da esfera. Sendo assim, a derivada da temperatura no centro é zero.
Então, bora lá:
- Condição de contorno 1: fluxo de calor zero no centro.
Já encontramos no Passo 1, a expressão da derivada da temperatura:
Note que, ao avaliarmos a equação na posição , o termo com a constante tende ao infinito. Como a derivada não pode tender ao infinito, a constante deve ser zero pra cancelar a contribuição desse termo:
Passo 3
Além disso, as maçãs estão suscetíveis a convecção do ar que escoa sobre elas, logo a condição de contorno em é de convecção na superfície. Dá uma olhada:
- Condição de contorno 2: convecção na superfície.
Substituindo a expressão da derivada da temperatura avaliada em , ficamos com:
Logo:
Antes de substituir os valores, bora converter a taxa volumétrica () pra unidade no SI:
Substituindo os valores do enunciado e a taxa convertida em SI:
Em graus Celcius:
Passo 4
Agora a gente só precisa determinar a temperatura do centro! Avaliando o perfil de temperatura no centro:
Logo:
Avaliando o perfil em na superfície:
Assim, isolando a temperartuta do centro ():
Substituindo os valores:
Em graus Celcius:
Resposta
Exercício Resolvido #5
Questão 3, PUCRIO, P1-2005
Um tubo de diâmetro interno igual a e espessura igual a , tem comprimento igual a . Uma resistência elétrica gera calor dentro da parede do tubo a uma taxa igual a:
A parede externa do tubo perde calor para o ambiente, que está a e transfere calor para o fluido interno, a uma taxa igual a . Considere regime permanente e condução apenas na direção radial.
Determine:
A distribuição de temperaturas na parede do tubo.
O fluxo de calor por condução ao longo do raio (em W).
A posição onde ocorre a temperatura máxima da parede.
Passo 1
A distribuição de temperaturas na parede do tubo.
A equação de calor para sistemas cilíndricos é dada por:
Considerando regime permanente e condução apenas na direção radial, teremos:
Partiu resolver essa equação diferencial:
Integrando dos dois lados:
Onde .
Integrando novamente dos dois lados:
Passo 2
Para descobrir os valores de e , basta utilizar as condições de contorno, onde há convecção na parede externa e um fluxo térmico constante na parede interna, logo:
Dessa forma, utilizando a primeira condição de contorno:
Utilizando a segunda condição de contorno:
Finalmente, a distribuição de temperatura é dada por:
Passo 3
O fluxo de calor por condução ao longo do raio (em W).
O fluxo de calor é dado por:
Derivando a expressão da temperatura que acabamos de encontrar:
Mas aí, repara que o fluxo de calor é dado em . E o que ele quer é em . Então temos que multiplicar esse cara pela área interna, que é:
Então:
Passo 4
A posição onde ocorre a temperatura máxima da parede.
A posição será dada por:
Dessa forma:
Resposta
Exercício Resolvido #6
Questão 3, UFF, P1-2017.1
(Adaptado) Rejeitos radioativos são colocados em um recipiente esférico de parede delgada. Os rejeitos geram energia térmica por unidade de volume de forma não uniforme de acordo com a relação . Onde é o raio do recipiente e uma constante.
Mantidas as condições de regime estacionário pela imersão do recipiente em um líquido que se encontra a e que fornece um coeficiente convectivo uniforme.
Determine a distribuição de temperaturas no interior do recipiente. Expresse seu resultado em termos de , , , e (condutividade térmica do rejeito).
Passo 1
A equação de calor para um sistema esférico é dada por:
Como o problema nos disse para considerar regime estacionário, e considerando que o fluxo de calor se dá somente na direção radial, a equação de calor pode ser simplificada para:
Substituindo a expressão da geração de calor, teremos:
Passo 2
Vamos agora resolver a equação, beleza?
Multiplicando os dois lados por , teremos:
Integrando dos dois lados em relação a :
Dividindo ambos os lados por :
Integrando novamente em relação a :
Agora temos que descobrir as constantes e . Para isso, vamos precisar das condições de contorno.
Passo 3
- Condição de contorno 1: fluxo de calor zero no centro.
Nós encontramos a expressão de no passo anterior.
Se liga que, ao avaliarmos a equação na posição , o termo com a constante tende ao infinito. Como a derivada não pode tender ao infinito, a constante deve ser zero pra cancelar a contribuição desse termo, logo:
![]()
Passo 4
- Condição de contorno 2: convecção na superfície.
Onde:
E, usando a expressão da derivada:
Assim:
Reorganizando os termos pra isolar :
Assim:
Resposta
Exercício Resolvido #7
Questão 1, UFRJ, P1-2008.1
Considere um cabo elétrico longo, de raio e condutividade térmica , no qual calor é uniformemente gerado com uma taxa volumétrica de . Este cabo é revestido com uma camada de plástico de de espessura e condutividade térmica de .
O plástico está em contato perfeito com a superfície do cabo elétrico. A temperatura da superfície externa do plástico é de . No regime permanente, calcule:
Temperatura na interface entre o cabo e o plástico;
Temperatura no centro do cabo.
O revestimento plástico reduz ou aumenta a temperatura na superfície do cabo? Justifique sua resposta.
Passo 1
Temperatura na interface entre o cabo e o plástico;
Pra calcular a temperatura na interface, devemos calcular a taxa de transferência de calor. Nesse sistema, o calor está sendo gerado pelo próprio fio. Assim:
Onde é o raio do fio. Dessa forma:
Podemos calcular a temperatura na interface entre o cabo e o plástico utilizando o conceito de resistência térmica, onde:
Onde é a resistência térmica de condução através do isolante de raio externo , dada por:
Dessa forma:
Passo 2
Temperatura no centro do cabo.
Para calcular a temperatura no centro do cabo, vamos ter que resolver a equação de calor para o sistema com geração de energia.
A equação de calor para sistemas cilíndricos, considerando que regime permanente será dada por:
Onde, como condições de contorno, temos fluxo térmico nulo no centro do fio e temperatura constante para . Dessa forma:
Integrando a equação calor, teremos:
Utilizando a nossa primeira condição de contorno, temos que .
Integrando novamente a equação:
Utilizando a segunda condição de contorno:
Assim:
Como queremos saber a temperatura no centro, para :
Passo 3
O revestimento plástico reduz ou aumenta a temperatura na superfície do cabo? Justifique sua resposta.
O revestimento não interfere na temperatura do cabo porque ele não dá, nem retira calor. O revestimento na verdade irá interferir na taxa de transferência de calor do sistema.
Resposta
O revestimento não interfere na temperatura na superfície do cabo.