Escoamento em Placa Plana
Produzido por Giovanna RonzéTeoria
Introdução
Agora que já estamos voando em convecção, estamos prontos pra jogar com os grandes!

Como o próprio título adiantou, estamos preocupados aqui somente com o escoamento em placa plana.
O que queremos aqui é entender como determinar o coeficiente convectivo pra diferentes situações! Basicamente, vamos dividir esse conteúdo em situações onde consideramos a temperatura da placa constante, e onde consideramos o fluxo térmico constante. Show?
Antes de seguirmos em frente, uma coisa muito importante!!! Nós vamos ver aqui uma série de correlações, as equações têm uns números bem esquisitos, mas a boa notícia é que você não precisa decorar as equações!

Vou colocar todas elas aqui mas, se precisar delas durante uma prova, o seu livro (Ozisik, Incropera, Çengel, etc) com certeza tem essas correlações. O que precisamos saber é como as escolhes e aplicá-las. De boa?!
As correlações vão nos dar o número de Nusselt e, a partir desse cara, a gente calcula o coeficiente convectivo .
Relaxa, no final eu vou lançar um passo-a-passo diferenciado pra você!
Então partiu!
Escoamento sobre uma Placa Isotérmica
Esse é o caso que vimos até esse momento, onde consideramos que toda a placa tem uma temperatura constante. Então, a ideia é essa:
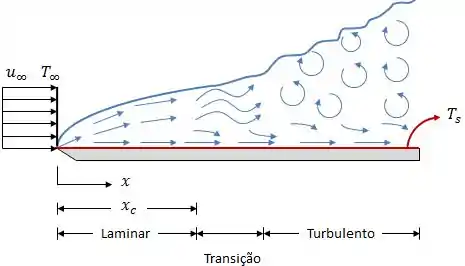
Para esse caso, quando precisarmos pegar os dados do fluido na tabela, vamos utilizar a temperatura de filme , dada por:
![]()
Pra facilitar a nossa vida, eu montei essa tabelinha para a gente!
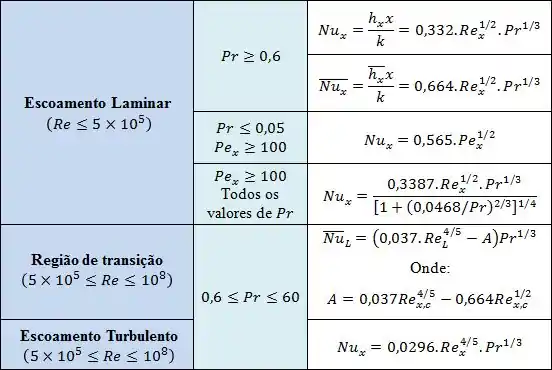
Onde é o número de Peclet, definido por .
No regime laminar, os números de Nusselt local e médio estão relacionados da seguinte forma:
![]()
“Opa! Mas o intervalo do número de Reynolds é o mesmo para a região de transição e o Escoamento Turbulento! Qual deles eu uso?!”
Cara! Muito boa a sua pergunta! Então, se estivermos interessados em calcular o coeficiente pontual, vamos utilizar a equação do escoamento turbulento, e se quisermos calcular o coeficiente médio , usamos a equação para a região de transição. Beleza?
Ainda sobre a região de transição, se considerarmos o número de Reynolds crítico![]() na equação para o número de Nusselt médio. Dessa forma, teremos que:
na equação para o número de Nusselt médio. Dessa forma, teremos que:
![]()
Caso o escoamento seja turbulento em toda a placa (ou quando temos uma pequena parte da placa com escoamento laminar), podemos calcular o número de Nusselt médio através da seguinte expressão:
![]()
Viu como as equações são esquisitas?
Se você ficar muito tempo olhando pra elas, é capaz dos seus olhos começarem a suar. Mas como eu disse antes, basta calcular o número de Reynolds, ver o valor do número de Prandtl e escolher a equação mais adequada pra resolver a nossa vida. :)
Escoamento sobre uma Placa com Fluxo Térmico Preescrito
Na real, esse não é um caso que aparece tanto mas, não estamos muito na vibe de dar margem pro azar, certo?
A ideia agora é basicamente essa:
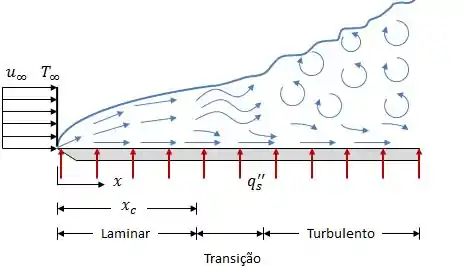
Então vou lançar aqui uma tabela muito parecida com o que vimos antes, ok?
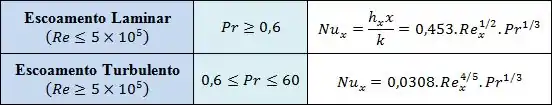
Como temos o fluxo de calor , podemos calcular a taxa de transferência de calor sem esquentar muito a cabeça:
Dessa forma, acaba não sendo necessário calcular o coeficiente convectivo médio . No entanto, nós podemos calcular a temperatura superficial média , dada por:
Onde .
Então, fique esperto pra ver se o problema vai ter dar uma placa com temperatura constante, ou com fluxo térmico constante, combinado?
Passo-a-passo diferenciado
“Peguei um problema de convecção externa, o que eu faço?!”
Como o objetivo final quando trabalhamos com convecção é calcular justamente o coeficiente convectivo , vamos fazer o seguinte:
- Identifique a geometria do escoamento: Estamos trabalhando com um escoamento sobre uma placa plana, esfera ou cilindro?
- Identifique a temperatura de referência: No caso de uma placa isotérmica, essa temperatura é a temperatura de filme. Utilize essa temperatura pra pegar os dados sobre o fluido, incluindo o número de Prandtl.
- Calcule o número de Reynolds: Utilize o número de Reynolds pra determinar se o escoamento é laminar ou turbulento.
-
Escolha a correlação adequada a partir dos valores de e . Lembrando que:
- O coeficiente local é usado para determinar o fluxo em um ponto específico;
- O coeficiente médio é usado para determinar a taxa de transferência de calor em toda a superfície.
- Calcule o coeficiente convectivo .
- Seja feliz! :)
Vamos aplicar isso na prática?! ;)
Escoamento sobre uma Placa Isotérmica
Escoamento sobre uma Placa com Fluxo Térmico Preescrito
Passo-a-passo diferenciado
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma placa plana, com largura de , é mantida a uma temperatura superficial uniforme pelo uso de módulos retangulares geradores de calor, com espessura e comprimento , que são controlados independentemente. Cada módulo encontra-se isolado de seus vizinhos, bem como em sua superfície inferior.
Ar atmosférico a escoa sobrea a superfície da placa a uma velocidade de . As propriedades termofísicas dos módulos são , e .
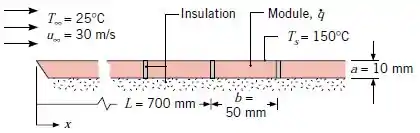
Determine a geração de energia necessária, , em um módulo posicionado a uma distância de da aresta frontal.
Determine a temperatura máxima neste módulo de geração.
Passo 1
Determine a geração de energia necessária, , em um módulo posicionado a uma distância de da aresta frontal.
Vamos nessa! Queremos encontrar a geração de energia , , para isso considerando o balanço de energia, temos:
Sabendo que:
e
Substituindo, as expressões a cima, podemos calcular :
Passo 2
Agora, que sabemos como calcular precisamos achar o coeficiente médio de convecção ():
O problema nos deu as propriedades do módulo, mas não nos deu as propriedades do ar. Assim, usando a temperatura de filme como referência, temos que:
Sabendo a temperatura de filme, podemos achar as propriedades do ar.
De acordo com a tabela A.4 do Incropera, temos que:
Passo 3
Com as propriedades dos fluidos em mãos, podemos calcular o número de Reynolds:
Como estamos interessados no módulo a da aresta frontal, . Dessa forma:
Opa! . O escoamento não é laminar nessa região!
Passo 4
A questão agora é a seguinte! Como estamos interessados em calcular a taxa de transferência de calor do módulo localizado a da aresta frontal da placa, não é uma boa usarmos a expressão para o número de Nusselt médio, porque ele vai nos dar o coeficiente convectivo médio ao longo de todos os .
Nesse caso, o coeficiente convectivo médio desse módulo que estamos interessados vai ser aproximadamente igual ao coeficiente convectivo local no centro desse módulo.
Então, vamos utilizar o número de Nusselt local no centro do módulo.
Já calculamos o número de Reynold para , mas agora estamos interessados em uma nova posição, no centro do módulo que tem comprimento .
Dessa forma, vamos calcular o novo número de Reynolds, agora para :
Como sabemos que o escoamento é turbulento em toda placa, vamos usar a seguinte correlação:
Substituindo os valores:
Passo 5
O coeficiente convectivo médio no módulo será, então:
Substituindo os valores:
Passo 6
Agora que achamos finalmente temos todas as variáveis necessárias pra calcular a geração de energia necessária (, que será:
Passo 7
Determine a temperatura máxima neste módulo de geração.
O fluxo de energia gerada no módulo deve ser igual ao fluxo de calor por condução no mesmo.
Partindo do princípio que a energia é gerada no centro do módulo, a temperatura será máxima neste mesmo ponto, a uma distância da superfície do módulo. Logo:
Reorganizando a equação:
Substituindo os valores:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Seja uma placa plana sujeita a um escoamento paralelo (superior e inferior) caracterizado por , .
Determine os coeficientes de transferência de calor por convecção médios e as taxas de transferência de calor por convecção associadas a uma placa plana com um comprimento e largura , para o escoamento de ar e temperaturas superficiais e .
Determine os coeficientes de transferência de calor por convecção médios e as taxas de transferência de calor por convecção associadas a uma placa plana com um comprimento e largura , para o escoamento de água e temperaturas superficiais e .
Passo 1
Logo de cara, tanto para a letra , quanto a para a letra , vamos determinar as propriedades que vamos usar ao longo do problema, beleza?
Pra diferenciais, vou chamar os resultados referentes à temperatura superficial de de 1, e para a temperatura superficiais de , de 2.
Letra – Ar
Temperatura de filme:
De acordo com a tabela A.4 do Incropera:
Letra – Água
Temperatura de filme:
De acordo com a tabela A.6 do Incropera:
Show! Agora podemos seguir em frente!
Passo 2
Determine os coeficientes de transferência de calor por convecção médios e as taxas de transferência de calor por convecção associadas a uma placa plana com um comprimento e largura , para o escoamento de ar e temperaturas superficiais e .
Precisamos do número de Reynolds pra escolher a correlação adequada:
De acordo com os números de Reynolds, não estamos no regime laminar.
Passo 3
Como estamos interessados em calcular os coeficientes convectivos médios, vamos utilizar a correlação para a região de transição, considerando . Logo:
Passo 4
Os coeficientes convectivos médios serão:
![]()
![]()
Passo 5
Como há troca de calor nas superfícies superior e inferior, a taxa total de transferência de calor será:
![]()
![]()
Passo 6
Determine os coeficientes de transferência de calor por convecção médios e as taxas de transferência de calor por convecção associadas a uma placa plana com um comprimento e largura , para o escoamento de água e temperaturas superficiais e .
Começando pelo número de Reynolds:
De acordo com os números de Reynolds, não estamos no regime laminar.
Passo 7
Como estamos interessados em calcular os coeficientes convectivos médios, vamos utilizar a correlação para a região de transição, considerando . Logo:
Passo 8
Os coeficientes convectivos médios serão:
![]()
![]()
Passo 9
Como há troca de calor nas superfícies superior e inferior, a taxa total de transferência de calor será:
![]()
![]()
Resposta
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Considere uma aleta retangular que é usada para resfriar o motor de uma motocicleta. A aleta possui de comprimento e está a uma temperatura de , quando a motocicleta desloca-se a uma velocidade de em ar a .
O ar encontra-se em escoamento paralelo às superfícies da aleta e condições de escoamento turbulento podem ser admitidas ao longo de toda a superfície.
Qual é a taxa de remoção de calor por unidade de largura da aleta?
Passo 1
A primeira coisa que temos que fazer aqui é determinar as propriedades do ar à temperatura de filme , que é a nossa referência.
De acordo com a tabela A.4 do Incropera:
Passo 2
Nesse caso, nem precisamos calcular o número de Reynolds pra escolher a correlação que vamos usar. Isso porque o próprio problema já nos disse que o ar encontra-se em condições de escoamento turbulento.
E, para situações onde temos escoamento turbulento sobre toda a placa, a correlação adequada é essa aqui:
Passo 3
O coeficiente convectivo médio será dado por:
Substituindo os valores:
Passo 4
Como o ar escoa pelos dois lados da aleta retangular, a taxa de transferência de calor por unidade de largura será:
Substituindo os valores:
![]()
Resposta
![]()
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Placas de aço (AISI 1010), de espessura e lados de comprimento , são transportadas na saída de um processo de tratamento térmico e simultaneamente resfriadas por ar atmosférico com velocidade e em escoamento paralelo sobre as placas.
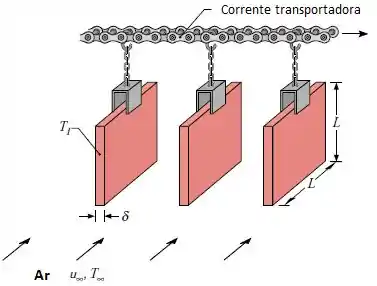
Para uma temperatura da placa inicial de , qual é a taxa de transferência de calor saindo da placa? Qual é a taxa de variação da temperatura da placa correspondente? A velocidade do ar é muito maior do que a velocidade da placa.
Passo 1
Antes de qualquer coisa, precisamos definir as propriedades dos materiais.
Para o aço (AISI 1010), vamos usar como referência a temperatura inicial da placa . Dessa forma, de acordo com a tabela A.1 do Incropera:
Já para o ar, vamos usar como referência a temperatura de filme . De acordo com a tabela A.4 do Incropera:
Passo 2
Para calcular a taxa de transferência de calor, vamos precisar do coeficiente convectivo médio mas, antes disso, precisamos calcular o número de Reynolds pra decidir qual correlação vamos usar:
Logo, vamos usar a correlação de para escoamento laminar.
Passo 3
A correlação adequada é a seguinte:
Substituindo os valores:
Passo 4
O coeficiente convectivo médio será dado por:
Passo 5
Finalmente, a taxa de transferência de calor será dada por:
Como o ar escoa pelos dois lados da placa, , onde corresponde à área de cada lado da placa. Logo:
![]()
Passo 6
Fazendo o balanço de energia na placa, temos que:
Como não temos energia entrando e sendo gerada na placa:
Dessa forma:
Reorganizando os tempos da equação, a taxa de variação da temperatura da placa correspondente será:
Substituindo os valores:
Resposta
![]()
![]()
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Cem componentes elétricos, cada um dissipando , estão fixados a superfície de uma placa quadrada de cobre , e toda a energia dissipada é transferida para a água que se encontra em escoamento paralelo sobre a superfície oposta.
Uma protuberância na aresta frontal da placa atua na perturbação da camada-limite e a placa pode ser considerada isotérmica. A velocidade e a temperatura d água são e , e as propriedades termofísicas da água podem ser aproximadas por , e .
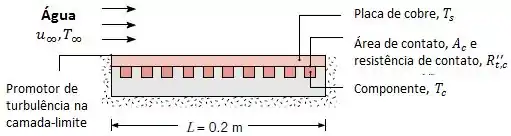
Qual é a temperatura da placa de cobre?
Se cada componente possui uma área superficial de contato com a placa de cobre igual a e a resistência térmica de contato é igual a , qual é a temperatura dos componentes? Despreze a variação de temperatura ao longo da espessura da placa de cobre.
Passo 1
Qual é a temperatura da placa de cobre?
Da equação da taxa de transferência de calor por convecção, temos que:
Podemos reorganizar essa equação e encontrar a temperatura na superfície da placa:
Show de bola! Precisamos calcular o coeficiente convectivo médio pra resolver o problema.
Passo 2
Nesse caso, o problema foi até bom com a gente, porque ele já nos deu as propriedades da água e nos disse que o escoamento ao longo de toda a placa é turbulento. Ou seja, podemos utilizar a seguinte expressão para o número de Nusselt médio:
Substituindo os valores:
Passo 3
O coeficiente convectivo médio será dado por:
Passo 4
Substituindo o valor de na expressão que chegamos no Passo 1, teremos:
Obs.: Multiplicamos a taxa de transferência de calor por 100 pois estamos trabalhando com cem componentes elétricos.
Passo 5
Se cada componente possui uma área superficial de contato com a placa de cobre igual a e a resistência térmica de contato é igual a , qual é a temperatura dos componentes? Despreze a variação de temperatura ao longo da espessura da placa de cobre.
Levando em conta a resistência de contato, a taxa de transferência de calor através de cada componente será dada por:
Reorganizando a equação, teremos:
Substituindo os valores:
Obs.: .
![]()
Resposta
![]()
Exercício Resolvido #6
Questão 2, PUCRIO, P2-2003
O número de Nusselt médio no escoamento laminar sobre uma superfície plana rugosa de comprimento igual a 1m, é dado por:
Determine qual dentre dois fluidos (A e B) deve ser escolhido para resfriar a placa, considerando que a taxa de calor transferido deve ser a mesma com os dois fluidos. Justifique sua resposta. As propriedades dos fluidos são dadas na tabela abaixo:

Passo 1
Se a taxa de calor transferido deve ser a mesma para os dois fluidos, o coeficiente convectivo deve ser o mesmo para os dois fluidos.
O coeficiente convectivo está associado como o número de Nusselt pela seguinte equação:
Substituindo a expressão dada pelo problema:
Onde é dado por:
E o número de Prandtl é dado por:
Assim, o coeficiente convectivo será:
Já que ambos os fluidos precisam de um mesmo coeficiente convectivo, o fluido mais apropriado será o que necessitar de menor velocidade de bombeamento (já que, gastaríamos menos energia pra bombeá-lo).
Passo 2
Igualando as expressões do coeficiente convectivo dos dois fluidos, teremos:
Arrumando um pouco a casa:
Com a casa arrumada, basta substituir os valores:
Assim, o fluido B é o mais adequado por necessitar de menor velocidade de bombeamento.
Resposta
O fluido B é o mais adequado por necessitar de menor velocidade de bombeamento.
Exercício Resolvido #7
Questão 3, PUC, Lista 2
(Adaptado) No processo de secagem de duas superfícies de mesmas dimensões (comprimento e largura ), mas com diferentes rugosidades, o regime de escoamento do ar sobre a superfície (na direção longitudinal) é turbulento.
As temperaturas das superfícies são , e longe dela a temperatura do fluido é . Na superfície 1, o coeficiente de troca de calor é dado por: ; e na superfície 2, , todos os valores em unidades SI. Para as duas situações, determine:
O número de Nusselt médio nas superfícies, .
Determine a taxa de calor total trocado por cada placa .
Passo 1
O número de Nusselt médio nas superfícies, .
Para calcular o número de Nusselt médio nas superfícies, precisamos dos coeficientes convectivos médios, dados por:
Assim, para a superfície 1:
Para a superfície 2:
Passo 2
Os números de Nusselt médio nas superfícies serão:
Onde é a condutividade térmica do ar à temperatura de filme, dada por:
A essa temperatura, de acordo com a tabela A.4 do Incropera, .
Logo:
![]()
![]()
Passo 3
Determine a taxa de calor total trocado por cada placa .
A taxa de calor será dada por:
Substituindo os valores:
![]()
![]()
Resposta
;
;
Exercício Resolvido #8
Questão 3, UFF, P2-2017.1
Uma placa plana quadrada de de lado tem uma de suas faces imersa em um meio com ar a que escoa paralelamente a placa com uma velocidade de . A outra face está exposta a uma chama. Essa chama está a e um coeficiente de película de pode representar a transferência de calor homogênea na área dessa face.
A placa é feita de aço inoxidável 304, as propriedades do aço podem ser consideradas constantes e iguais a seus valores a e essa placa possui uma espessura de .
Considerando que o sistema está em estado estacionário e que a radiação térmica pode ser desprezada. E sabendo que as propriedades termofísicas do ar podem ser obtidas pela tabela anexa do livro de referência e que esse se comporta como gás ideal.
Determine a temperatura na superfície de cada face da placa e a taxa de transferência de calor associada ao sistema.
Passo 1
A estratégia aqui é a seguinte: ao invés de começar calculando as temperaturas pra depois calcular a taxa de transferência de calor, vamos fazer o contrário.
Para isso, vamos analisar o problema como o seguinte circuito térmico:
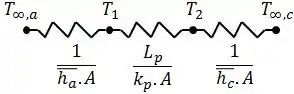
Onde os índices , e correspondem ao ar, à placa e à chama, respectivamente, e e representam as temperaturas das faces da placa.
Nesse caso, a taxa de transferência de calor será:
Onde a resistência térmica equivalente é dada por:
De acordo com a tabela A.1 do Incropera, para o aço inoxidável 304 a , a condutividade térmica será:
Repare que, da equação resistência térmica equivalente, o único valor que não conhecemos é o coeficiente convectivo entre a placa e o ar. Então vamos atrás dele.
Passo 2
Esse se trata de um problema de convecção externa. Assim, as propriedades do ar deveriam ser dadas à temperatura de filme, dada por:
Mas como não temos , vamos utilizar aqui a temperatura de , que o problema nos deu para calcular as propriedades do aço.
Assim:
Assim, utilizaremos os dados tabelados para . De acordo com a tabela A.4 do Incropera, para o ar a esta temperatura:
Passo 3
O número de Reynolds, será:
Opa! Como estamos interessados em calcular o coeficiente convectivo médio, vamos usar a correlação do número de Nusselt para a região de transição (considerando ), dada por:
Substituindo os valores:
Assim, o coeficiente convectivo entre a placa e o ar será:
Passo 4
A resistência térmica equivalente do circuito será:
Passo 5
A taxa de transferência de calor será:
Passo 6
A temperatura na parede em contato com o ar será:
Substituindo os valores:
Passo 7
A temperatura na parede em contato com a chama será:
Substituindo os valores:
Resposta
Exercício Resolvido #9
Questão 2, UFF, P2-2015.1
Uma placa plana de de espessura feita de chumbo (com propriedades constantes e dadas pelo valor dessas a ) está com uma de suas faces sob uma chama que fornece a ela . A placa é quadrada com de lado. Pela outra face, uma corrente de ar a escoa paralelamente a . O sistema está a .
Se for possível, em quanto tempo a temperatura vai atingir ? Se não for possível atingir , qual é a temperatura máxima da placa?
Assuma modelo de parâmetros concentrados para resolver o problema.
As propriedades termofísicas do ar são dadas na tabela.
Passo 1
Assumindo o modelo de parâmetros concentrados, consideramos que a temperatura no interior da placa é uniforme.
Fazendo o balando de energia, temos que:
Como o corpo não gera calor por si só, a gente fica com:
Onde o calor entra por conta do fluxo térmico da chama, e o calor sai por conta da convecção entre a placa e o ar. Dessa forma:
Resolvendo a equação acima, teremos:
Essa é uma equação diferencial linear que pode ser resolvida pelo método do fator integrante.
O fator integrante é dado por:
Pra simplificar a equação, vou chamar todo o termo constante dentro da integral de . Dessa forma:
Assim, a nossa equação diferencial terá a seguinte cara:
Onde é uma constante qualquer. Reorganizando a equação e substituindo a expressão de :
Vamos determinar essa constante mais à frente usando a condição inicial do problema, quando formos substituir os valores.
Pra seguir em frente, precisamos calcular o coeficiente convectivo.
Passo 2
Antes de calcular o coeficiente convectivo, precisamos das propriedades do ar. Como a temperatura da placa irá variar entre e , vamos usar a média dessas temperaturas pra calcular a temperatura de filme. Assim:
Assim, de acordo com a tabela A.4 do Incropera:
Para o chumbo, considerando a temperatura de , teremos:
Passo 3
Esse é um problema de convecção sobre uma placa plana. Assim, o número de Reynolds será:
Logo, como temos escoamento turbulento, a correlação mais adequada para o número de Nusselt será:
O coeficiente convectivo será:
Passo 4
Voltando à expressão que encontramos no Passo 1:
Aplicando a condição inicial de que, para , , teremos:
Substituindo os valores:
Passo 5
Como queremos calcular o tempo necessário para que a placa atinja , vamos reorganizar a equação:
Substituindo os valores:
O termo no interior do logaritmo será negativo. Como isso não pode ocorrer, significa que a temperatura da placa nunca chegará a .
Passo 6
A temperatura máxima da placa será dada para . Assim:
![]()
Resposta
A temperatura da placa nunca chegará a .
Exercício Resolvido #10
Questão 2, UFRJ, P2-2015.2
A superfície de um coletor solar pode ser considerada como uma placa plana, com dimensões de . A temperatura desta superfície é praticamente uniforme e de .
Ar a escoa sobre a placa ao longo de seu comprimento, com velocidade de . Calcule:
Coeficiente médio de transferência de calor sobre a placa;
Coeficiente local de transferência de calor em ;
Fluxo de calor local em ;
Taxa de calor trocado entre a placa e o ar.
Passo 1
Antes de qualquer coisa, precisamos das propriedades do ar. Usando a temperatura de filme como referência, temos que:
De acordo com a tabela A.4 do Incropera, temos que:
Passo 2
Coeficiente médio de transferência de calor sobre a placa;
Agora que já temos as propriedades do fluido, podemos calcular o número de Reynolds:
O regime é turbulento. Supondo escoamento turbulento em toda a placa, o número de Nusselt médio será:
Finalmente, o coeficiente convectivo médio será:
![]()
Passo 3
Coeficiente local de transferência de calor em ;
O número de Nusselt local é dado por:
Assim, o coeficiente convectivo será:
![]()
Passo 4
Fluxo de calor local em ;
O fluxo de calor será dado por:
![]()
Passo 5
Taxa de calor trocado entre a placa e o ar.
Nesse caso, como extamos interessados na taxa de calor, vamos usar o coeficiente convectivo médio.
![]()
Resposta