Equação da Energia e Bernoulli
Teoria
Opaa, seja muito bem vindo ao Responde Aí! Bora bater um papo sobre equação da energia! Pela primeira lei da termodinâmica podemos calcular a variação de energia de um sistema usando a seguinte fórmula:
Onde
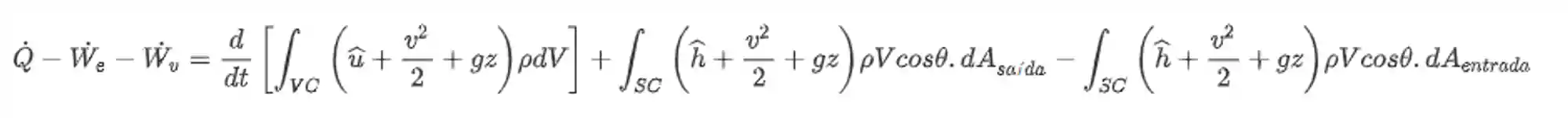
Como assim??!! 😱😱😱
📢 Clique para saber mais:
- Equações Básicas na Forma Integral para um Volume de Controle
- Equação da Quantidade de Movimento
- Livros Resolvidos
Calma, dificilmente a gente vai usar essa equação ai de cima. Tem muuuitas simplificações pela frente e a gente também vai entender o significado de cada termo! Pra começar com tudo, que tal você conferir esse vídeo super completo que o Responde Aí preparou pra você?
A primeira coisa que podemos fazer para simplificar a nossa equação é considerar o regime permanente, dessa forma temos:
Onde:
⇒ Fluxo de calor ⇒ Fluxo de trabalho de eixo ⇒ Fluxo de trabalho de outras fontes ⇒ Fluxo de massa ⇒ Entalpia ⇒ Velocidade ⇒ gravidade ⇒ altura
Para melhorar nossa situação podemos considerar conservação de massa:
Podemos também dividir toda equação pela vazão mássica, assim obtendo:
Essa equação ainda está em termos de propriedade térmicas como h que representa a entalpia. Assim, alguns estudiosos fizeram várias transformações para chegar numa forma simplificada da equação de energia:
Equação da Conservação da Energia para o Volume de Controle
Finalmente chegamos em uma equação que vamos usar bastante! A equação abaixo compara a energia entre duas superfícies:
Onde
é a perda de carga é a carga fornecida pela bomba é a carga consumida pela turbina
Equação de Bernoulli
A Equação de Bernoulli é uma simplificação da equação de conservação de energia. Nela consideramos o fluido incompressível e em escoamento permanente, sem bomba ou turbina. Podemos escrever a equação de Bernoulli da seguinte forma:
Onde
Porque os aviões voam?
Pra ficar mais claro vamos dar uma olhada no desenho da asa de um avião:
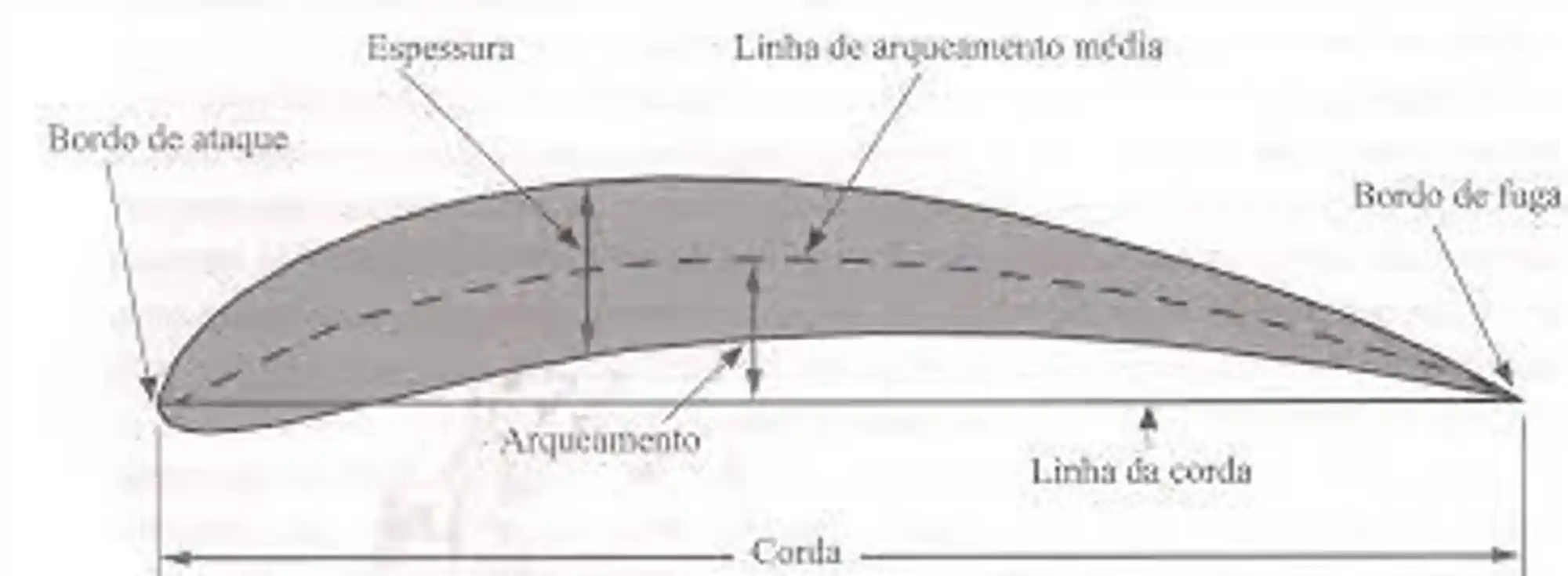
Imagina uma quantidade pequenininha de ar na ponta esquerda da asa, uma parte dela vai passar por cima da asa e outra por baixo. Beleza? Mas esse é um regime permanente, então a fração de ar que passa por cima da asa deve chegar no ponto final junto com a fração que passa por baixo da asa.
O problema é que o trajeto superior é maior que o trajeto inferior, pra resolver esse problema a velocidade da fração de ar que passa por cima da asa vai ser maior e consequentemente a pressão vai ser menor. Resumindo temos:
Se a pressão em baixo da asa é maior que a pressão em cima da asa, então a tendência do avião é ficar suspenso no ar!
Agora vamos praticar com exercícios?!
Equação da Conservação da Energia para o Volume de Controle
Equação de Bernoulli
Porque os aviões voam?
Exercícios Resolvidos
Exercício Resolvido #1
Uma central de energia às margens de um rio, como na figura abaixo, deve eliminar de calor perdido para o rio. As condições do rio a montante são e . O rio tem de largura e de profundidade. Se as perdas de calor para a atmosfera e para o solo são desprezíveis, calcule as condições do rio a jusante .
Passo 1
Vamos começar escolhendo nosso volume de controle. Nesse caso é interessante que a central de energia esteja dentro do nosso volume de controle.
Agora podemos montar a equação de energia, nesse caso temos apenas calor sendo dissipado. Se lembrarmos da equação de calor é , como estamos sempre falando de fluxo de calor:
O fluxo de massa é igual e podemos abrir ele como .
Como o fluxo de massa são iguais, temos que a vazão de entrada é igual a vazão de saída.
Em uma tabela de vemos que o da água é
Resposta
Exercício Resolvido #2
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 502, ex. 8.80
(Adaptada) Água escoa em um tubo horizontal de área transversal constante; o diâmetro do tubo é 75 mm e a velocidade média do escoamento é 5 m/s. Na entrada do tubo, a pressão manométrica é 275 kPa e a saída é à pressão atmosférica. Determine a perda de carga no tubo.
Passo 1
Nesse exercício temos um tubo horizontal. Isso quer dizer que a elevação na entrada e na saída do escoamento é a mesma:
Além disso, ao dizer que a velocidade média do escoamento é 5 m/s, podemos dizer que a velocidade de entrada e saída são iguais a esse valor:
Podemos trabalhar com pressão manométrica ou absoluta. O importante é que se escolhermos utilizar manométrica, teremos que usá-la para e . Se escolhermos usar absoluta, teremos que usá-la para e .
Só não vale misturar manométrica com absoluta, combinado? Vou escolher usar manométrica aqui:
Podemos finalmente ir para a equação da energia!
Passo 2
A equação da energia é:
Nesse caso não temos bomba nem turbina, então e
Como e , esses termos serão cancelados
Assim, podemos perceber que nesse caso, a perda de carga está relacionada apenas à queda de pressão. Substituindo os valores:
Encontramos a perda de carga!
Resposta
Exercício Resolvido #3
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 502, ex. 8.79
(Adaptada) Medidas foram feitas para a configuração de escoamento de água mostrada na figura. Na entrada, seção 1, a pressão é 70kPa (manométrica), a velocidade média é 1,75 m/s e a elevação é 2,25 m. Na saída, seção 2, a pressão, a velocidade média e a elevação são, respectivamente, 45 kPa (manométrica), 3,5 m/s e 3 m, respectivamente. Calcule a perda de carga em metros.
Passo 1
Primeiro, vamos anotar direitinho quem é quem. Na entrada (seção 1), temos:
Já na saída (seção 2), temos:
Opa! Então o enunciado nos deu todos os dados de pressão, velocidade e elevação. Com a equação da energia, vamos conseguir calcular a perda de carga que foi pedida.
Passo 2
A equação da energia é:
Como não há bomba nem turbina no nosso volume de controle (que já foi definido na figura do enunciado), então e . Atualizando a equação da energia:
Vamos substituir os valores separados no Passo 1 e calcular a perda de carga
Lembrando que o fluido é a água
Encontramos a perda de carga! :D
Resposta
Exercício Resolvido #4
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 502, ex. 8.81
Para a configuração de escoamento da figura, é sabido que a perda de carga é 1 m. Da entrada para a saída, a queda de pressão é 50 kPa, a velocidade dobra da entrada para a saída, e o aumento de elevação é de 2 m. Calcule a velocidade de entrada da água.
Passo 1
Dessa vez o enunciado deu as variáveis da equação da energia de uma forma um pouquinho diferente. O primeiro passo é escrever quem são essas variáveis.
Pela figura, vemos que a seção 1 corresponde à entrada e a seção 2 à saída.
O é negativo pois houve uma queda de pressão, ou seja, . Logo, podemos reescrever essa relação:
Agora sim, vamos para a equação da energia!
Passo 2
A equação da energia é:
Lembrando que, como não tem bomba nem turbina no volume de controle, então e . Logo, a equação da energia fica:
E agora, reorganizando os termos para podermos substituir o que encontramos pelo enunciado:
Substituindo:
Logo, a velocidade de entrada é 3,7 m/s
Resposta
Exercício Resolvido #5
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Quando a bomba da figura abaixo bombeia de água a do reservatório, a perda de carga total por atrito é de . O escoamento descarrega através de um bocal para a atmosfera. Calcule a potência da bomba em entregue para a água.
Passo 1
Vamos começar definindo as superfícies de analise de energia.
Assim, temos superfície na superfície do reservatório e uma superfície na saída do fluido.
Precisamos descobrir quanto vale e para isso vamos usar o fato do enunciado nos ter fornecido a vazão da bomba. Como o fluido é a água o fluido é incompressível e por isso podemos falar que a vazão que a bomba impõe é igual à vazão de saída.
E a velocidade com que o reservatório desce?? Se liga nessa dica, ela vai ser muito usada.
Em questões de reservatório se considera que o volume de água é tão mais tão grande que sua altura não muda, assim .
Agora vamos aplicar a equação de conservação de energia. Como a vazão mássica é igual, podemos escrever o sistema como vimos na teoria:
Agora vamos considera nosso eixo na superfície , assim
A pressão em é a pressão atmosférica e a pressão em também é .
é a perda por fricção ou atrito, assim o enunciado nos disse que vale
Então ficamos com a seguinte equação
Mas queremos a potencia da bomba, assim temos que lembrar que a potencia de uma bomba é dada por:
Resposta
Exercício Resolvido #6
A bomba da figura abaixo cria um jato d’água a , orientado para atingir uma distância horizontal máxima. As perdas por atrito do sistema são de . O jato pode ser aproximado pela trajetória de partículas sem atrito. Que potência a bomba deve entregar à água?
Passo 1
Pra resolver esse exercício, precisamos da equação de energia.
E para aplicar essa equação, vamos ter que definir o volume de controle, com limites onde temos bastante informações.
Então vamos posicionar o nosso ponto 1 de controle na superfície do reservatório e o ponto 2 na saída do tubo, no início do lançamento.
No ponto 1, consideramos:
Já no ponto 2, vamos ter:
O nosso , porque colocamos a origem do nosso eixo z nessa altura ok?
E já sacamos que vamos ter que determinar aquela velocidade ali que tá faltando.
Passo 2
O problema aqui é você sacar que pra alcançar a distância horizontal máxima a inclinação do lançamento deve ser . Isso não é óbvio, mas como você está fazendo esse exercício, já vai saber na próxima vez que precisar disso.
E com essa informação, vamos usar Torricelli para saber a velocidade do jato de água no inicio do lançamento.
Na altura máxima a velocidade em é zero (já que ele para de subir e começa a descer), assim, temos que:
Aí a gente tem a componente da velocidade no eixo z, que é igual a velocidade total vezes o sem de , que a gente definiu como 45°. E a aceleração no eixo z é a gravidade mesmo.
Passo 3
Agora que temos a velocidade em 2, podemos voltar para a equação da energia.
Que com o que a gente tem até agora:
Onde , as perdas por atrito.
A gente pode, então, cortar aqueles termos iguais e reorganizar um pouco a galera:
Pra achar:
Como queremos a potência da bomba:
Resposta
Exercício Resolvido #7
Um jato de álcool atinge a placa vertical da figura abaixo. Uma força é necessária para manter a placa estacionária. Considerando que não há perdas no bocal, calcule o fluxo de massa de álcool e a pressão absoluta na seção .
Passo 1
Fazendo a analise de momento linear na direção , chegamos em: (esse resultado é melhor explicado em um exercício da teoria de momento linear).
Como o enunciado falou , temos que a velocidade será:
Tendo a velocidade em , conseguimos calcular a vazão mássica.
Passo 2
Agora vamos usar a conservação se massa para encontrar
Agora por Bernoulli sem perdas pois nesse caso não há nenhuma perda, podemos escrever a equação:
Como o escoamento não muda de altura temos que
Podemos cortar e multiplicar por
Resposta
Exercício Resolvido #8
Considere a turbina extraindo energia através de um conduto forçado em uma barragem, como na figura abaixo. Para escoamento turbulento em dutos, a perda de carga por atrito é aproximadamente , em que a constante depende das dimensões do conduto forçado e das propriedades da água. Mostre que, para uma dada geometria de conduto forçado e vazão variável do rio, a máxima potência possível da turbina nesse caso é e ocorre quando a vazão é .
Passo 1
Nessas questões, temos que primeiro escolher as superfícies que vamos usar para estudar a energia.
Iremos analisar a superfície que é a superfície do maior reservatório e a superfície que é a superfície do líquido após passar pela turbina. Isso vai nos permitir fazer algumas simplificações.
Lembra que quando tratamos de reservatórios vamos considerá-los tão grandes que a altura da superfície não varia? Assim .
Vamos colocar nosso eixo na superfície . Assim e .
E ambas superfícies estão expostas a pressão atmosféricas.
Então escrevendo a equação de energia temos:
Passo 2
E retirando aquele termo que tá repetido dos dois lados:
Isolamos o porque, afinal, é a potência da turbina que vamos querer estudar. E a potência da turbina está correlacionada com o , que é a carga consumida pela turbina.
O enunciado nos definiu que .
A potência da turbina a gente viu lá na teoria que é:
Então:
Passo 3
Tudo muito lindo, mas e agora?
O problema fala de pressão máxima, certo? Como descobrimos o máximo de uma função??
Sim, temos que derivar e igualar a zero. Assim:
Então descobrimos que a turbina vai ter potência máxima quando .
E nesse caso a potência será de:
Resposta
Ei, a resposta está no passo a passo :)