Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 81
O coeficiente convectivo associado ao escoamento de um fluido sobre uma esfera sólida pode ser determinado pela imersão da esfera, inicialmente a 25°C, no interior do escoamento a 75°C e a medida de sua temperatura superficial em algum instante de tempo durante o processo transiente de aquecimento.
(a) Se a esfera tem um diâmetro de 0,1 m, uma condutividade térmica de 15 W/(m · K) e uma difusividade térmica de m²/s, em que instante de tempo a temperatura superficial de 60°C será registrada se o coeficiente convectivo for de 300 W/(m² · K)?
(b) Avalie o efeito do valor da difusividade térmica na resposta térmica do material calculando os históricos das temperaturas no centro e na superfície da esfera para α = , e m²/s. Represente graficamente os seus resultados para o período 0 ≤ t ≤ 300 s. De maneira análoga, avalie o efeito da condutividade térmica considerando valores de k = 1,5; 15 e 150 W/(m · K).
Passo 1
Tá legal! A primeira coisa que devemos fazer é calcular o número de Biot para esse caso, então, teremos:
Então, não poderemos usar o método da capacitância global, já que o número de Biot não é pequeno o suficiente. Vamos então usar a aproximação para condução unidimensional em uma esfera.
Passo 2
Para isso vamos utilizar a equação 5.53a vista nesse capítulo, onde temos:
Isolando dessa equação, chegamos em:
Agora, encontrando o termo , temos:
E, calculando , como estamos interessados na superfície, temos:
Passo 3
Agora, vamos precisar das constantes e que se encontram na tabela 5.1, para isso, precisamos antes calcular o número de Biot, então, teremos:
Então, para esse número de Biot, temos as seguintes constantes:
Então, substituindo os valores conhecidos na equação para , temos:
Então, como temos , a solução aproximada é válida, então, através da equação exata de , que é dada por:
Isolando o tempo dessa equação, temos:
Substituindo os valores conhecidos, chegamos em:
Passo 4
Agora para a letra (b) nós vamos utilizar as expressões dos passos anteriores, só que, precisamos de um auxílio de software para resolver de maneira iterativa. No entanto, o procedimento adotado deve ser pegar a equação de aproximação descrita no passo 2:
Vamos substituir as expressões para e , para deixar em função do tempo e das temperaturas na superfície e no centro, então, temos:
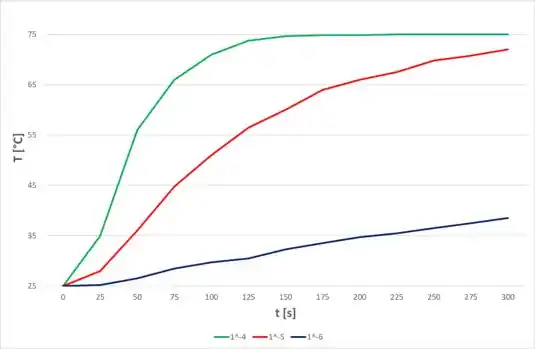
Então, utilizando essa expressão, para diferentes valores de , no intervalo de , para a temperatura no centro da esfera, temos:
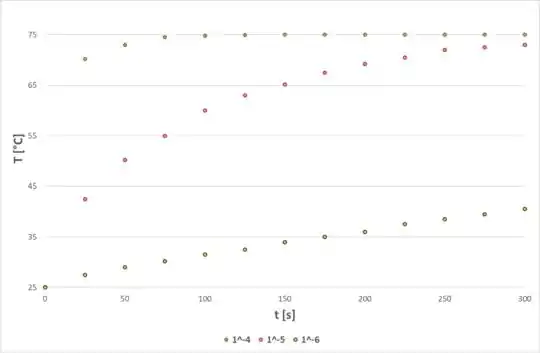
Agora, da mesma forma, para a temperatura na superfície, temos:
Passo 5
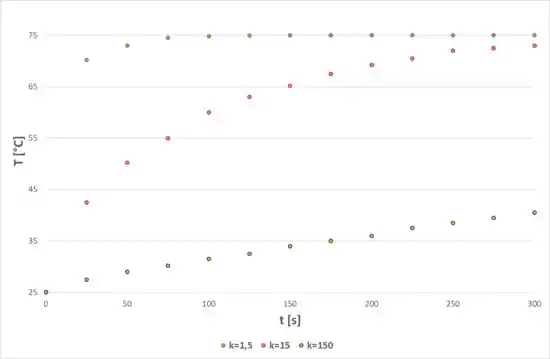
Agora, da mesma forma, vamos fixar o valor de , que foi o valor utilizado para cálculo na letra (a) e vamos variar o valor de . Dessa forma, para a temperatura no centro, temos o seguinte gráfico:
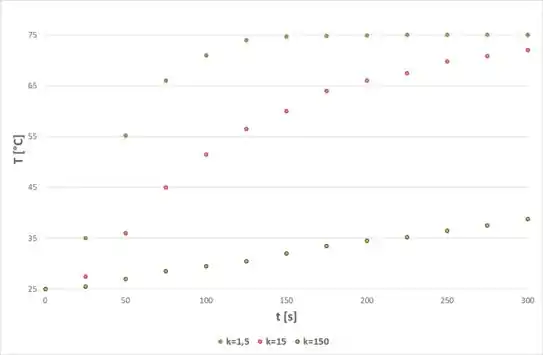
E a temperatura na superfície será:
