Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 66

Considere uma aleta plana triangular, bidimensional, com comprimento L = 50 mm e espessura na base de t = 20 mm. A condutividade térmica da aleta é k   =   25 W m K . A temperatura de sua base é T b   =   50 ° C e a aleta esta exposta a condições convectivas caracterizadas por h   =   50 W m 2 K e T ∞ = 20 ° C . Usando uma malha de diferenças finitas com Δx = 10 mm e Δy = 2

mm, e aproveitando a simetria, determine a eficiência de aleta, η a . Compare o seu valor para a eficiência da aleta com o informado na Figura 3.19.

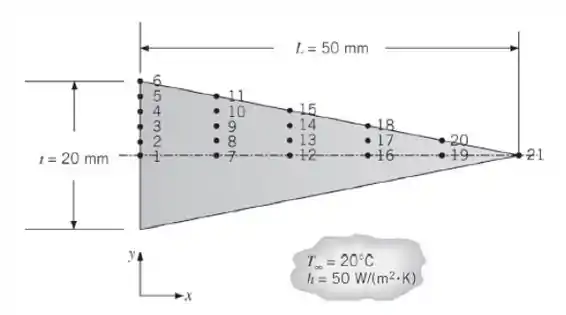
Passo 1

Boom galerinha, vamos começar?

Para desenhar o que está acontecendo aqui, nós precisamos lembrar que:

Δ x   =   10   m m

Δ y   =   2   m m

E:

Δ l = Δ x 2 + Δ y 2 = 10   m m 2 + 2 m m 2

Δ l = 10,198   m m

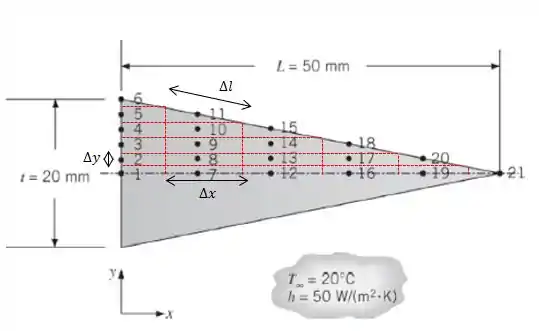
Nós queremos calcular a eficiência da aleta, certo?

Vamos dar uma olhadinha na fórmula?

η a = q ' a h A a θ b

Se:

h   =   50 W m 2 K

θ b = T b - T ∞ = 50 ° C - 20 ° C = 30 ° C

E a área desta aleta triangular pode ser dada como:

A a = 2 L 2 + t 2 2 = 2 0,05   m 2 + 0,02   m 2 2 = 0,102   m

A única coisa que precisamos é do calor da aleta, certo?

E nós também podemos usar uma fórmula, né? Mas não se esqueçam que dividimos a aleta em duas partes:

q ' a = 2 k ∆ y ∆ x T 1 - T 7 2 + T 2 - T 8 + T 3 - T 9 + T 4 - T 10 + T 5 - T 11 2

q ' a = 0,2 25 W m K T 1 - T 7 + 2 T 2 - 2 T 8 + 2 T 3 - 2 T 9 + 2 T 4 - 2 T 10 + T 5 - T 11

Pela figura nós vemos que:

T 1 = T 2 = T 3 = T 4 = T 5 = T 6 = 50 ° C

Então:

q ' a = 5 W m k - T 7 - 2 T 8 - 2 T 9 - 2 T 10 - T 11 + 400

Agora nós só precisamos das temperaturas, bora calcular?

Passo 2

Os nós no interior são calculados usando a fórmula:

T i = 1 4 ∑ T v i z i n h o s

Vamos começar?

4 T 7 = T 1 + 2 T 8 + T 12

4 T 8 = T 2 + T 7 + T 13 + T 9

4 T 9 = T 3 + T 8 + T 14 + T 10

4 T 10 = T 4 + T 9 + T 15 + T 11

4 T 12 = T 6 + 2 T 13 + T 16

4 T 13 = T 8 + T 12 + T 17 + T 14

4 T 14 = T 9 + T 13 + T 18 + T 15

4 T 16 = T 12 + 2 T 17 + T 19

4 T 17 = T 13 + T 16 + T 20 + T 18

4 T 19 = T 16 + 2 T 20 + T 21

Os demais pontos sofrem convecção, ok?

No Ponto 11:

h ∆ l k + 2 T 11 = T 5 + T 10 + h ∆ l k T ∞

Calculando o termo h ∆ l k :

h ∆ l k = 50 W m 2 K 0,01 0198   m 25 W m K = 0,02

Então:

2,02 T 11 = T 5 + T 10 + 0,4

No Ponto 15:

2,02 T 15 = T 10 + T 14 + 0,4

No Ponto 18:

2,02 T 18 = T 14 + T 17 + 0,4

No Ponto 20:

2,02 T 20 = T 17 + T 19 + 0,4

No Ponto 21:

h ∆ l k + 1 T 21 = T 19 + h ∆ l k T ∞

Então:

1 , 02 T 21 = T 19 + 0,4

Agora nós podemos achar as temperaturas:

T 7 = 47,6 ° C

T 8 = 47,6 ° C

T 9 = 47,59 ° C

T 10 = 47,58 ° C

T 11 = 47,57 ° C

T 12 = 45,3 ° C

T 13 = 45,3 ° C

T 14 = 45,29 ° C

T 15 = 45,28 ° C

T 16 = 43,11 ° C

T 17 = 43,11 ° C

T 18 = 43,10 ° C

T 19 = 41,03 ° C

T 20 = 41,03 ° C

T 21 = 39,09 ° C

Passo 3

Já que temos as temperaturas basta nós calcularmos o calor:

q ' a = 5 W m k - 47,6 ° C - 2 47,6 ° C - 2 47,59 ° C - 2 47,58 ° C - 47,57 ° C + 400

q ' a = 109 W m

E com o calor nós conseguimos achar a eficiência:

η a = 109 W m 50 W m 2 K 0,102   m 30 ° C

η a = 0,71

Nós também temos que comparar este valor para a eficiência da aleta com o informado na Figura 3.19.

Vamos dar uma olhadinha?

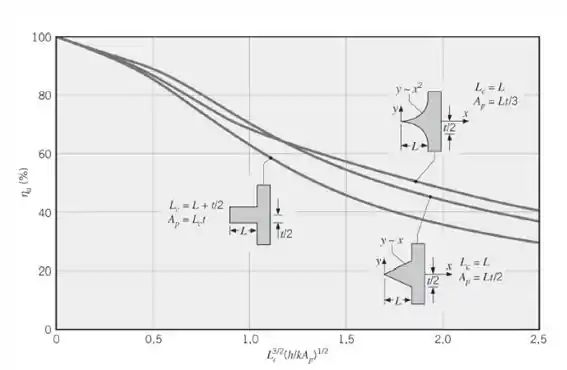
Para isso vamos calcular o eixo x:

L c 3 2 h k A p 1 2 = L 3 2 2 h k L t 1 2

Substituindo:

L c 3 2 h k A p 1 2 = 0,05   m 3 2 2 50 W m 2 K 25 W m k 0,05   m 0,02   m 1 2 = 0,707

Olhando no gráfico:

η a = 0,78

Então, quando nós comparamos o valor calculado e o valor da figura percebemos que eles são bem próximos, não é?

E assim nós acabamos mais uma !!

Resposta

η a = 0,71

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja o elemento combustível do Exemplo 5.11, que opera a uma taxa volumétrica de geração uniforme de 1 = 107 W/m3, até que a taxa de geração mude subitamente para 2 = 2 × 107 W/m3. Use o software de e
Considere o sistema do Problema 4.86. Inicialmente, a placa cerâmica ( α = 1,5×10 - 6m 2 / s ) se encontra a uma temperatura uniforme de 30 ° C . Subitamente, os elementos elétricos de aquecimento são
Duas barras muito longas (na direção normal à página) com as distribuições iniciais de temperaturas mostradas na tabela, devem ser soldadas lateralmente uma à outra. No tempo t=0 , a face equivalente
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Deduza a equação de diferenças finitas, bidimensional e transiente, para a temperatura no ponto nodal 0 localizado sobre a fronteira entre dois materiais diferentes.