Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 85
Considere uma parede plana composta constituída por três materiais (materiais , e organizados da esquerda para a direita) de condutividade térmica , e . As espessuras das três camadas da parede são , e . Há uma resistência de contato de na interface entre os materiais e , assim como na interface entre os materiais e . A face esquerda da parede composta é isolada termicamente, enquanto a face direita está exposta a condições convectivas caracterizadas por e . No Caso 1, energia térmica é gerada no material a uma taxa de . No Caso 2, energia térmica é gerada no material C a uma taxa de .
(a) Determine a temperatura máxima no interior da parede composta sob condições de regime estacionário para o Caso 1.
(b) Esboce a distribuição de temperaturas em coordenadas , em estado estacionário, para o Caso 1.
(c) Esboce a distribuição de temperaturas, em estado estacionário, para o Caso 2 nas mesmas coordenadas usadas para o Caso 1.
Passo 1
Nessa questão, queremos encontrar (a) temperatura máxima no interior da parede para o Caso 1, (b) esboçar a distribuição de temperaturas em coordenadas em estado estacionário para o caso 1, (c) esboçar a distribuição de temperaturas, em estado estacionário, para o Caso 2 em coordenadas .
PRESSUPOSTOS:
(1) condições de estado estacionário;
(2) transferência de calor unidimensional;
(3) geração uniforme de energia volumétrica.
DADOS FORNECIDOS:
Temperatura do fluido externo:
Coeficiente convectivo:
Condutividade térmica da parede A:
Condutividade térmica da parede B:
Condutividade térmica da parede C:
Espessura da parede A:
Espessura da parede B:
Espessura da parede C:
Resistência de contato:
Caso 1
Energia térmica é gerada no material :
Caso 2
Energia térmica é gerada no material C: .
Passo 2
(a) Para resolver essa questão, podemos fazer o seguinte esquema para a parede composta de dos materiais A, B e C.
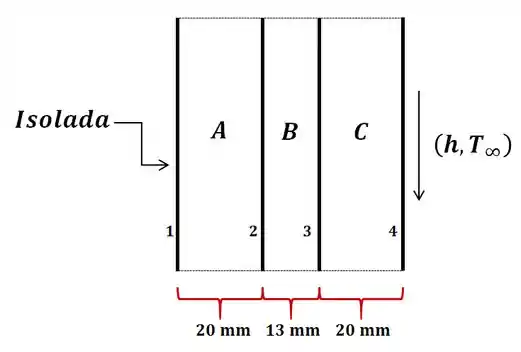
No caso 1, temos que o lado esquerdo da parede é isolado e o lado direito da parede é exposto ao ambiente tendo assim convecção. Para o caso 1, onde a energia térmica é gerada em material A, podemos desenhar o circuito de rede térmica equivalente, como mostrado abaixo:
Aqui, é a resistência de contato térmico entre os materiais A e B, B e C, é a resistência de condução no material B, é a resistência de condução no material C.
Passo 3
Para resolver essa questão é importante saber que sob condições de estado estacionário, a quantidade de calor gerada na parede A é igual à taxa de calor conduzida na parede composta. Ou seja:
Aqui, é a quantidade de calor gerado no material A e é o volume da parede A.
Com o circuito de rede térmica equivalente, podemos escrever a equação de condução de calor do material A até a extremidade direita da parede. Assim temos:
Substituindo a taxa de calor conduzida, podemos encontrara temperatura da seguinte maneira:
Substituindo os termos da equação acima pelos dados fornecidos, temos:
Passo 4
Temos que a temperatura máxima ocorre em e pode ser avaliada usando a Eq. 3.48. Assim temos:
Substituindo os termos da equação acima pelos dados obtidos, temos:
Portanto, a temperatura máxima dentro da parede composta para o caso 1, é .
Passo 5
(b) Agora, vamos encontrar as temperaturas em cada ponto da interface para esboçar a o gráfico da distribuição de temperatura para o estado estacionário. Temos que o fluxo de calor conduzido no material A, é igual no material B, é igual no material C e na convecção do lado direito da parede composta. Assim, podemos dizer que:
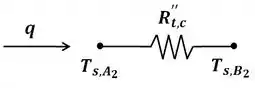
Substituindo os termos da equação acima pelos dados obtidos, temos:
Podemos dizer também que:
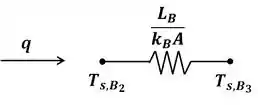
Substituindo os termos da equação acima pelos dados obtidos, temos:
Podemos dizer também que:
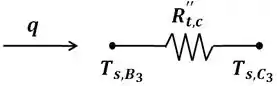
Substituindo os termos da equação acima pelos dados obtidos, temos:
Podemos dizer também que:
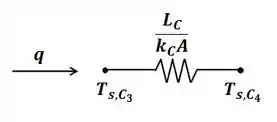
Substituindo os termos da equação acima pelos dados obtidos, temos:
Passo 6
Agora, podemos desenhar o esboço da distribuição de temperatura no estado estacionário, como mostrado abaixo.
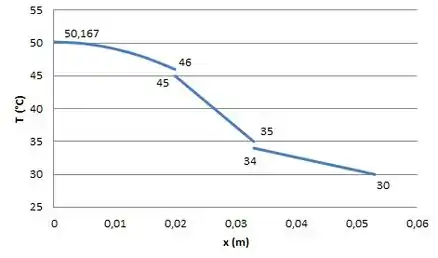
Passo 7
(c) Agora, vamos considerar o caso 2, onde a geração de calor ocorre no material C. No estado estacionário, não há calor conduzido da parede de material C para a parede de material A e B, pois a face esquerda é isolada e o calor não pode fluir. Então, vamos calcular a temperatura na superfície do material C exposta ao ambiente sabendo que o calor gerado na parede C é igual à transferência de calor por convecção externa. Ou seja:
Aqui, é a espessura do material C e é a temperatura da superfície no material C. Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 8
Temos que a temperatura máxima ocorre em e pode ser avaliada usando a Eq. 3.48. Assim temos:
Substituindo os termos da equação acima pelos dados obtidos, temos:
Passo 9
Agora, podemos desenhar o esboço da distribuição de temperatura no estado estacionário, como mostrado abaixo.
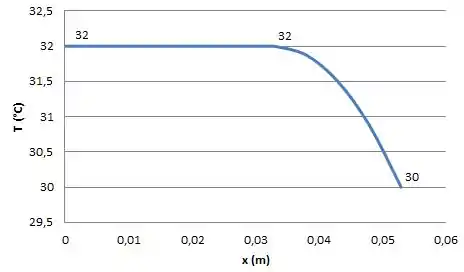
Resposta
(a)