Como um meio para aumentar a transferência de calor em circuitos integrados (chip) lógicos de alto desempenho, é comum a fixação de um dissipador de calor à superfície do chip, com o objetivo de aumentar a área superficial disponível para transferência de calor por convecção. Devido à facilidade de fabricação (efetuando cortes ortogonais em um bloco de material), uma opção atraente é a utilização de um dissipador de calor composto por aletas de seção quadrada com lado . O espaçamento entre aletas adjacentes é determinado pela largura da lâmina da serra. A soma deste espaçamento com a largura da aleta define o passo da aleta . O método utilizado para fixar o dissipador de calor ao chip determina a resistência de contato interfacial,.
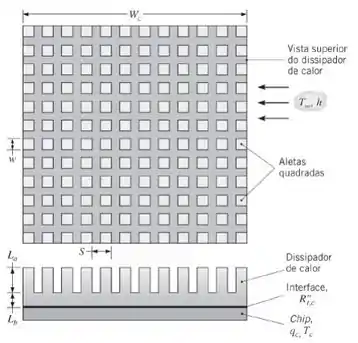
Seja um chip quadrado com largura e condições nas quais o resfriamento é feito por um líquido dielétrico com e O dissipador de calor é fabricado em cobre e suas dimensões características são e . Os valores especificados para e representam mínimos impostos por limitações de fabricação, bem como pela necessidade de manutenção de escoamento adequado nas passagens entre as aletas.
(a) Se uma junta metalúrgica fornece uma resistência de contato de e a temperatura máxima permissível do chip é de , qual é a potência máxima que o chip pode dissipar? Suponha que todo o calor seja transferido através do dissipador de calor.
(b) Pode ser possível aumentar a dissipação de calor pelo aumento de , sujeito à limitação de que , e/ou pelo aumento de (sujeito à limitação de fabricação de que ). Avalie o efeito de tais mudanças.
Passo 1
Aqui nós temos as dimensões do dissipador de calor de cobre e as condições de convecção. Onde o circuito térmico é:
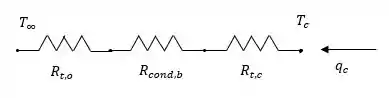
E queremos encontrar a dissipação de calor máxima permitida para uma temperatura específica do chip, resistência de contato interfacial do chip / dissipador de calor e o efeito do comprimento e largura da aleta na dissipação de calor.
Passo 2
Para resolver essa questão nós vamos assumir que:
(1) Estamos em condição de estado estacionário;
(2) A transferência de calor é unidimensional no conjunto de dissipador de calor de aletas;
(3) é constante;
(4) A resistência térmica do chip é desprezível;
(5) A transferência de calor da parte traseira do chip é desprezível;
(6) A temperatura do chip é uniforme.
Na letra (a), queremos calcular a potência máxima, que o chip pode dissipar. Para o sistema prescrito, a dissipação de energia do chip pode ser expressa como:
Onde,
A resistência térmica do conjunto de aletas é:
Onde,
E,
Passo 3
Com:
E,
Temos que:
A eficiência da aleta é:
Onde,
Então,
E,
Passo 4
Calculando agora a resistência térmica do conjunto de aletas, temos:
E a dissipação de calor máxima permitida é:
Passo 5
Na letra (b), queremos saber o efeito da dissipação de calor pelo aumento de , para isso vamos determinar em função de em quatro casos diferentes, cada um dos quais é caracterizado pelo espaçamento de aletas permitido mais próximo de
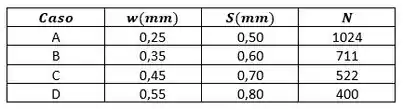
Com o aumento de e, portanto, a diminuição de , há uma redução na área total associada à transferência de calor da matriz de aletas. No entanto, para os casos A a C, a redução em é mais do que equilibrada por um aumento em (e ), causando uma redução em e, portanto, um aumento em .
À medida que a eficiência da aleta se aproxima de seu valor limite de , as reduções em devido ao aumento de não são mais equilibradas pelos aumentos em e começa a diminuir. Portanto, existe um valor ótimo de , que depende de . Para as condições deste problema, e fornecem a maior dissipação de calor.
Resposta
- Com o aumento de e, portanto, a diminuição de , há uma redução na área total associada à transferência de calor da matriz de aletas. À medida que a eficiência da aleta se aproxima de seu valor limite de , as reduções em devido ao aumento de não são mais equilibradas pelos aumentos em e começa a diminuir. Portanto, existe um valor ótimo de , que depende de .