Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 111
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a . O banho de óleo é bem misturado e isolado termicamente.
(a) Considerando que as propriedades do líquido de resfriamento são iguais às do óleo de motor a , determine a temperatura da esfera no regime estacionário.
(b) Deduza expressões em diferenças finitas explícitas para as temperaturas da esfera e do banho de óleo como funções do tempo usando um único ponto nodal tanto para a esfera quanto para o banho de óleo. Determine algum requerimento de estabilidade que possa limitar o tamanho do incremento no tempo.
(c) Determine as temperaturas da esfera e do banho de óleo após um incremento de tempo usando as expressões explícitas da parte
(b) e incrementos de tempo de e
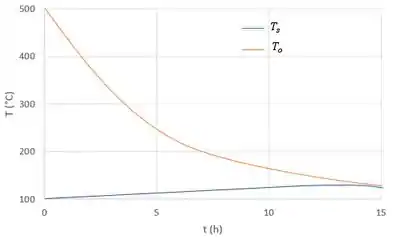
(d) Usando uma formulação implícita com , determine o tempo necessário para a esfera revestida atingir . Compare a sua resposta com o tempo associado com um banho muito grande, isolado termicamente. Represente graficamente as temperaturas da esfera e do óleo como funções do tempo na faixa . Sugestão: Veja o Comentário 3 do Exemplo 5.2.
Passo 1
No Problema 5.9 nós tínhamos o volume de uma esfera e do óleo. Além da temperatura inicial da esfera e óleo, o coeficiente de convecção, a espessura e condutividade térmica do revestimento de filme dielétrico.
Com isso, queremos achar a temperatura da esfera em estado estacionário, as expressões explícitas para as temperaturas da esfera e do óleo e os requisitos de estabilidade. O tempo necessário para que a esfera revestida atinja usando uma formulação e solução implícita de diferenças finitas e o gráfico da resposta térmica da esfera e do óleo.
Ufa! Muita coisa, mas vamos caminhar juntos que conseguimos chegar lá
Passo 2
Para resolver essa questão vamos assumir que:
(1) A camada dielétrica possui capacitância térmica desprezível em relação à esfera de aço;
(2) As propriedades são constantes;
(3) A resistência de contato é desprezível entre revestimento dielétrico e o aço;
(4) O banho de óleo é bem agitado;
5) O banho de óleo é bem isolado.
Os valores do aço e do óleo foram retirados da Tabela A-1. Na letra (a) queremos a temperatura da esfera no regime estacionário. Temos que é o coeficiente geral de transferência de calor que combina os efeitos da resistência de convecção e resistência de condução associados ao filme dielétrico. Isso é,
Onde,
Então,
Passo 3
O efeito do número de Biot é:
Desde o , uma abordagem de capacitância concentrada é apropriada para a esfera. Da mesma forma, como o óleo é bem misturado, uma abordagem de capacitância concentrada é apropriada para o óleo.
O volume da esfera é:
E o volume do óleo é:
Passo 4
A aplicação de balanços de energia na esfera e no óleo resulta em:
Onde é a temperatura no estado estacionário do óleo e da esfera. Reorganizando a equação, temos:
Substituindo os valores, temos:
Passo 5
Na letra (b) queremos algum requerimento de estabilidade que possa limitar o tamanho do incremento no tempo. Reconhecendo que a temperatura do óleo varia com o tempo a esfera produz:
Similarmente, para o óleo bem misturado, temos a expressão:
Nós queremos que o coeficiente de seja positivo. Então,
Passo 6
Na letra (c) queremos as temperaturas da esfera e do banho de óleo após um incremento de tempo. Substituindo os valores das propriedades, temperaturas iniciais e volumes nas equações anteriores para um passo de tempo temos:
Os resultados para várias etapas do tempo são:
A especificação de um intervalo de tempo maior que o critério de estabilidade leva a resultados irrealistas, conforme é mostrado na tabela acima.
Passo 7
Na letra (d) queremos representar graficamente as temperaturas da esfera e do óleo como funções do tempo na faixa . Como se encontra abaixo
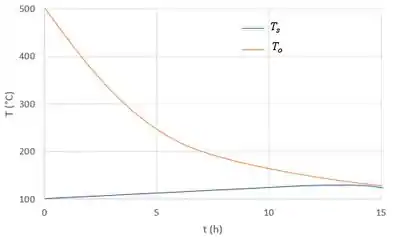
O tempo necessário para a esfera atingir uma temperatura de é . O tempo associado a um grande banho de óleo (temperatura constante do óleo) foi encontrado no Problema 5.9, usando o método de capacitância concentrada e é
Resposta
