Movimento Circular
Produzido por Ludovic BeghinTeoria
O Movimento Circular é o movimento angular que ocorre em uma trajetória circular.
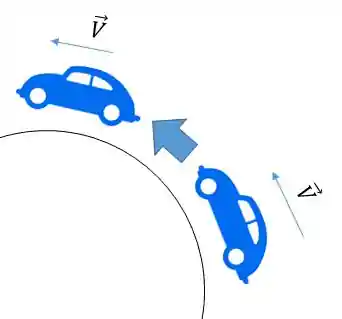
Na figura acima temos uma ilustração de um movimento circular, onde um carro esta fazendo uma curva. Nela podemos perceber que o vetor velocidade muda de direção no momento da curva.
Ou seja, mesmo que a velocidade seja constante em módulo, sua direção varia. Pois bem, guarda essa informação!
Hoje a gente vai conversar sobre movimento circular uniforme e movimento circular acelerado. Mas, você sabia que todo movimento circular possui aceleração centrípeta?!
-Quee?😖
É isso mesmo! Mas vamos entender melhor o que é a aceleração centrípeta!
Aceleração Centrípeta
A aceleração centrípeta é uma componente da aceleração perpendicular à trajetória e ela é responsável pela mudança de direção!
Assim:
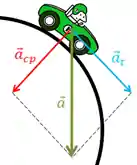
Ou seja, a aceleração centrípeta aponta para o centro da curva, sendo sempre perpendicular à velocidade. Ela pode ser calculado usando a seguinte fórmula:
Onde,
Ah, a aceleração centrípeta é incapaz de mudar o módulo da velocidade, agora faz mais sentido o MCU ter aceleração centrípeta e ser uniforme ao mesmo tempo! 🤣🤣🤣
Movimento Circular Uniforme (MCU)
No movimento circular uniforme o módulo da velocidade é constante, logo ela possui apenas a aceleração centrípeta, responsável por alterar a trajetória do objeto.
Existem alguns conceitos super importantes, que a gente PRECISA, conhecer antes de fazer qualquer cálculo de movimento circular!
Bora dar uma olhadinha neles?
Período
O período
Como no
Podemos também calcular a aceleração centrípeta a partir do período:
Frequência
Agora, a frequência é o número de voltas dadas em um intervalo de tempo. Ou seja, ela é igual ao inverso do período.
A gente também pode escrever a velocidade em função da frequência.
Deslocamento Angular
O deslocamento angular é a alteração no valor do ângulo quando realizamos um movimento circular.
Pra calcular o deslocamento angular, fazemos:
Velocidade Angular
A velocidade angular
Movimento Circular Acelerado (MCUV)
No movimento circular acelerado (MCUV), além da aceleração centrípeta, temos também a aceleração tangencial, dada por:
A aceleração resultante do corpo é calculada levando em conta a aceleração centrípeta e a aceleração tangencial:
Vídeo Aula - Movimento Circular
Ficou com alguma dúvida?!
Então se liga nesse resumo de movimento circular supercompleto em vídeo! 👇
📢Clique para saber mais:
- Movimento circular uniforme;
- Movimento circular acelerado;
- Velocidade e aceleração média;
- Velocidade e aceleração instantâneas
Agora vamos praticar com exercícios?!
Aceleração Centrípeta
Movimento Circular Uniforme (MCU)
Movimento Circular Acelerado (MCUV)
Vídeo Aula - Movimento Circular
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física I, P1-2012.2- Questão 8
Considere as seguintes afirmações sobre os vetores velocidade e aceleração de um corpo em movimento: A velocidade pode ser zero e a aceleração ser diferente de zero. O módulo do vetor velocidade pode ser constante, com o vetor velocidade mudando com o tempo. O vetor velocidade pode ser constante mas seu módulo pode variar com o tempo. O vetor velocidade pode mudar de sentido com o tempo mesmo que o vetor aceleração permaneça constante. São verdadeiras as afirmações:
- Todas as afirmações
- I, II e III
- II e III
- I, II e IV
- Nenhuma das afirmações anteriores.
Passo 1
Esse é um exercício puramente teórico, esses exercícios tem uma pegada diferente mas ajudam bastante a gente a ter um pensamento diferente em relação as questões, mais analítico. Vamos responder sobre cada a afirmação e pensar sobre elas.
Passo 2
“A velocidade pode ser zero e a aceleração ser diferente de zero” é Verdadeiro, Basta lembrarmos do lançamento vertical para cima, onde a velocidade na altura máxima e zero, porém a aceleração da gravidade ainda está atuando;
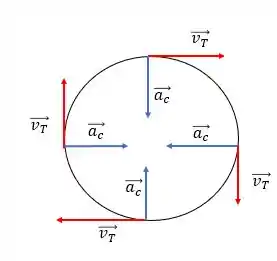
“O módulo do vetor velocidade pode ser constante, com o vetor velocidade mudando com o tempo” é Verdadeiro, no movimento circular uniforme é exatamente isso que acontece, temos a aceleração centrípeta mudando o vetor velocidade, no caso variando sua direção, mas o seu módulo permanece constante.
“O vetor velocidade pode ser constante mas seu módulo pode variar com o tempo.” é Falso, para o vetor ser constante ele precisa manter seu módulo constante. Um exemplo disso é o lançamento horizontal
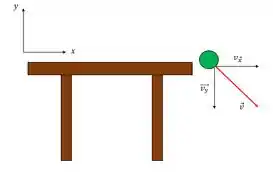
A velocidade em é constante mas em varia fazendo o módulo variar. A gente pode até analisar a fórmula do módulo pra observar essa relação:
“O vetor velocidade pode mudar de sentido com o tempo mesmo que o vetor aceleração permaneça constante.” É Verdadeiro, é o que acontece no lançamento vertical para cima, a aceleração é constante e na subida a velocidade aponta pra cima após chegar ao pico, a velocidade passa a apontar pra baixo e temos a descida do movimento, saca só:
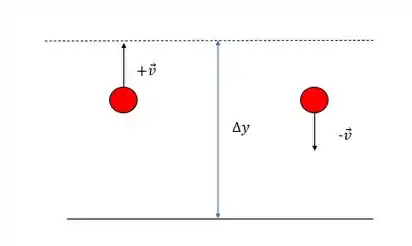
As corretas então são as afirmações:
- I, II e IV
Resposta
d)I, II e IV
Exercício Resolvido #2
IFGO
Podemos dizer que uma partícula se encontra em movimento quando suas posições sofrem alterações no decorrer do tempo em relação a um dado referencial. Estando em movimento, ainda podemos dizer que a partícula pode estar em movimento uniforme ou em movimento variado. Acerca de um satélite geoestacionário que se encontra sobre a linha do equador terrestre, podemos afirmar corretamente que
a) não possui aceleração pelo fato de sua velocidade ter módulo constante.
b) a aceleração tangencial é nula e a aceleração centrípeta dependerá da altitude que se encontrar em relação à superfície da Terra.
c) possui aceleração escalar constante e diferente de zero.
d) sua aceleração resultante é a própria aceleração tangencial.
e) a aceleração vetorial desse satélite não pode ser nula, pois o satélite deverá possuir velocidade tangencial muito grande.
Passo 1
Satélites se moivmentam na órbita da terra, ou seja, eles realizam um movimento circular, né? E se eles relizam esse movimento, eles possuem velocidade linear constante, como a gente viu lá na teoria! Sendo assim, como o módulo da velocidade linear não muda, a aceleração tangencial é nula, porque pra termos aceleração precisamos de uma variação na velocidade.
Passo 2
Por outro lado, existe uma aceleração centrípeta, certo? Porque ocorre uma mudança de direção e sentido do vetor velocidade, e podemos calcular essa aceleração assim:
Como podemos ver aí em cima, a aceleração centrípeta é inversamente proporcional ao raio da trajetória, portanto, a aceleração do satélite dependerá da altitude em que ele se encontra. Show!
Resposta
b) a aceleração tangencial é nula e a aceleração centrípeta dependerá da altitude que se encontrar em relação à superfície da Terra.
Exercício Resolvido #3
Brasil Escola - Adaptado
As afirmações a seguir tratam da aceleração centrípeta.
I – A aceleração centrípeta é responsável pela alteração da direção e do sentido do vetor velocidade.
II – A aceleração centrípeta pode ser definida como sendo o quadrado do módulo da velocidade dividido pelo raio da trajetória.
III – O vetor aceleração centrípeta possui a mesma direção e sentido do vetor velocidade.
Está correto o que se afirma em:
a) I e III
b) I e II
c) II e III
d) Apenas I
e) Apenas II
Passo 1
Vamos analisar as 3 afirmações e avaliar ao longo do exercício quais estão corretas, começando pela afirmação I.
I – A aceleração centrípeta é responsável pela alteração da direção e do sentido do vetor velocidade.
Aceleração centrípeta é responsável por alterar a direção e o sentido da velocidade, mas nunca o módulo dela, se liga nesse desenho de um corpo em movimento circular uniforme.
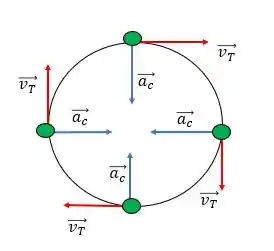
Onde é a aceleração centrípeta e é a velocidade tangencial do corpo.
Podemos ver que conforme o corpo faz o movimento sua direção vai se alterando sempre pro sentido da aceleração centrípeta do ponto anterior, mas o módulo da velocidade não muda.
Então nossa afirmação I tá correta!
Passo 2
A segunda afirmação diz que:
II – A aceleração centrípeta pode ser definida como sendo o quadrado do módulo da velocidade dividido pelo raio da trajetória.
A gente também viu na nossa teoria que:
.
Então o item II tá correto também!
Passo 3
Já a terceira afirmação diz o seguinte:
III – O vetor aceleração centrípeta possui a mesma direção e sentido do vetor velocidade.
E a gente pode olhar a mesma imagem usada no passo 1 pra ver se isso é verdade ou não.
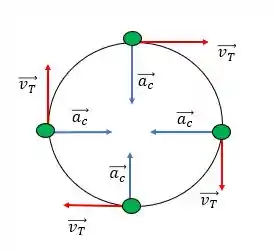
Se liga aí, a aceleração centrípeta aponta pro centro e a velocidade tangencial é tangente á trajetória, esses caras são perpendiculares portanto não tem mesma direção e por isso a afirmação III está errada.
Resposta
b) I e II
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 84. 4- Perguntas 13
A figura abaixo mostra quatro trilhos [semicírculos ou quartos de círculo) que podem ser usados por um trem que se move com velocidade escalar constante. Ordene os trilhos de acordo com o módulo da aceleração do trem no trecho curvo, em ordem descrescente.
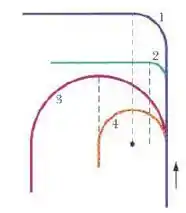
Passo 1
Ah, temos aqui 4 movimentos circulares. Podemos notar que os raios das trajetórias são diferentes entre si. O enunciado disse pra gente que a velocidade é constante, e como é o mesmo trem para cada curva será a mesma velocidade independente do raio da curva.
Sabendo disso a gente pode usar a equação da aceleração centrípeta e como a velocidade é constante só dependeremos do raio da trajetória pra ordenar as acelerações.
Como o raio está no denominador, quanto maior for o raio menor será a aceleração, beleza?
Passo 2
Vamos olhar a figura e ordenar o tamanho dos raios.
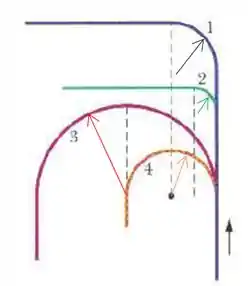
O menor raio aqui é o raio da curva , e se liga a geometria dela pouco importa, o que importa é o tamanho do raio, beleza?
Os raios das curvas e são iguais e maiores que o da curva 2, e como eu disse antes não importa a geometria dessas curvas e só o tamanho dos raios.
O raio da curva 3 é o maior de todos.
Sendo assim ordenamos os raios.
E a gente viu antes que o menor raio nos dará a maior aceleração centrípeta, então é só inverter essa ordem ai pras acelerações:
Resposta
Exercício Resolvido #5
UFAL
Um carro passa por uma elevação na pista com velocidade de módulo constante e igual a 10km/h. A elevação corresponde a um arco de uma circunferência de raio R=5m, centrada no ponto O.
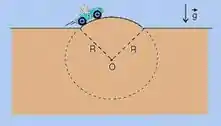
Considerando o carro como uma partícula material, qual a sua aceleração centrípeta, em , sobre a elevação?
a) 2b) 4c) 200d) 400e) 20.000
Passo 1
Bora lá! Como a gente já sabe, a aceleração centrípeta pode ser calculada assim:
E o enunciado nos deu o valor da velocidade e do raio, então é só aplicarmos na formulinha!
Mas lembra que queremos em km, e nosso raio tá em metros, então, como 5m=0,005km, vamo lá:
Prontinho! Tranquilo, né?
Resposta
e) 20.000
Exercício Resolvido #6
UFAL
Um objeto realiza um movimento circular e uniforme em uma circunferência com raio igual a 100m e com uma aceleração centrípeta de 4. Determine sua velocidade.
Passo 1
Como a gente já viu, a aceleração centrípeta é dada por:
Então vamo jogar na formulinha!
Showw!
Resposta
Exercício Resolvido #7
UFRJ, Física I, P1-2014.1- Questão 2
Um carro, considerável como uma partícula, sobre uma lombada circular de centro de curvatura em , como indica a figura. O módulo da velocidade do carro vai diminuindo à medida que ele sobe a lombada. Dadas as setas identificadas pelos números , , , e da figura, a que pode representar a aceleração do carro o ponto da subida indicado é a número
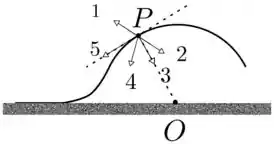
Passo 1
Neste caso temos um movimento circular. Isso nos diz que temos pelo menos aceleração centrípeta apontando para o centro da curva.
Porém, o enunciado também nos diz que o carro vai diminuindo sua velocidade, assim ele sofre uma aceleração tangencial também, fazendo a aceleração resultante do carro estar apontando para dentro do circulo, porém com uma leve inclinação.
Podemos ver essa representação no esquema abaixo
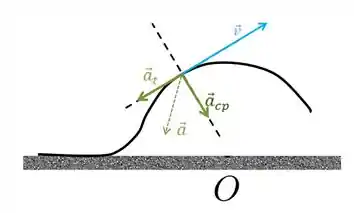
Resposta
c) 4
Exercício Resolvido #8
UFRJ, Física I, P1-2013.2 - Questão 4
Uma partícula em trajetória circular de raio tem um vetor aceleração que em um certo instante faz um ângulo com o vetor velocidade . Podemos afirmar que nesse instante
- O módulo da velocidade da partícula é igual a ;
- O módulo da velocidade da partícula é igual a ;
- A aceleração da partícula tem módulo ;
- O módulo da velocidade da partícula está aumentando;
- O módulo da velocidade da partícula está diminuindo;
Passo 1
No movimento circular, a velocidade é tangencial ao movimento.
Como a aceleração possui um ângulo de com a velocidade, significa que ela não é somente a aceleração centrípeta mas também tem a componente tangencial.
A aceleração tangencial é no mesmo sentido da velocidade isso porque o ângulo entre a velocidade e a aceleração é menor que .Vamos fazer um desenho para visualizar melhor.
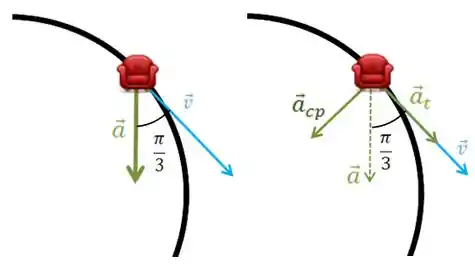
Repara no desenho, que a aceleração tangencial é no mesmo sentido que a velocidade então o módulo da velocidade está aumentando. Isso tá dito na opção (d)!
Passo 2
Vamos justificar por que as outras estão erradas?
A letra (e) tá errada por que ela fala o contrário da letra (d)!
Passo 3
As letras (a) e (b) dizem um certo valor pra velocidade! Como a trajetória é circular vamos ter que a velocidade se relaciona com a aceleração centrípeta
E a aceleração centrípeta é uma componente da aceleração, que, pela figura acima, é dada por
Assim
O que não tem nada a ver com as opções né? rsrsrs Nem na unidade tá batendo!
Passo 4
A aceleração da partícula tem duas componentes e podemos escrever o seguinte
Assim o módulo da aceleração será
Como
O módulo da aceleração da partícula será
Que seria se a aceleração tangencial fosse nula! Como não é, então o item (c) tá errado também!
Resposta
Letra D