Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Movimento Circular Uniformemente Variado (MCUV)

Ver Todos os Exercícios

Teoria

O Movimento Circular Uniformemente Variado (MCUV) é um movimento que ocorre em uma trajetória curva e tem aceleração tangencial constante.

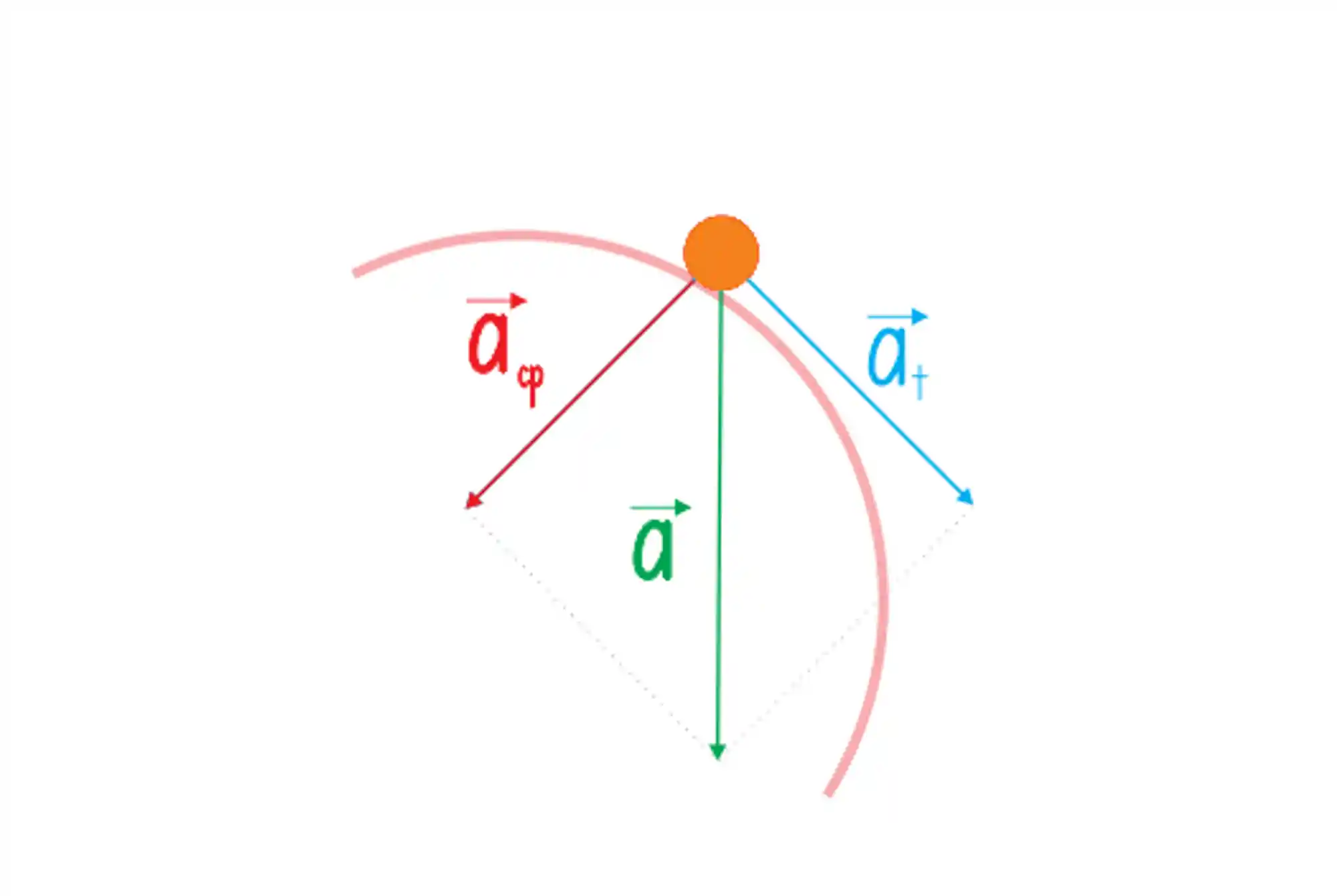
Movimento Circular Acelerado
Movimento Circular Acelerado

No movimento circular temos que considerar duas componentes da aceleração, a aceleração centrípeta e a aceleração tangencial. Enquanto a aceleração centrípeta aponta para o centro da curva e é responsável por mudar a trajetória do objeto, a aceleração tangencial é quem faz o módulo da velocidade escalar mudar!

Ou seja, a aceleração tangencial é a grande estrela do MCUV e já que o movimento é UNIFORMEMENTE variado, a aceleração tangencial será constante!

📢Clique para saber mais:

Fórmulas do Movimento Circular Uniformemente Variado (MCUV)

Agora vamos ao que interessa, bora conhecer as fórmulas do MCUV! Mas pra isso vamos usar um exemplo:

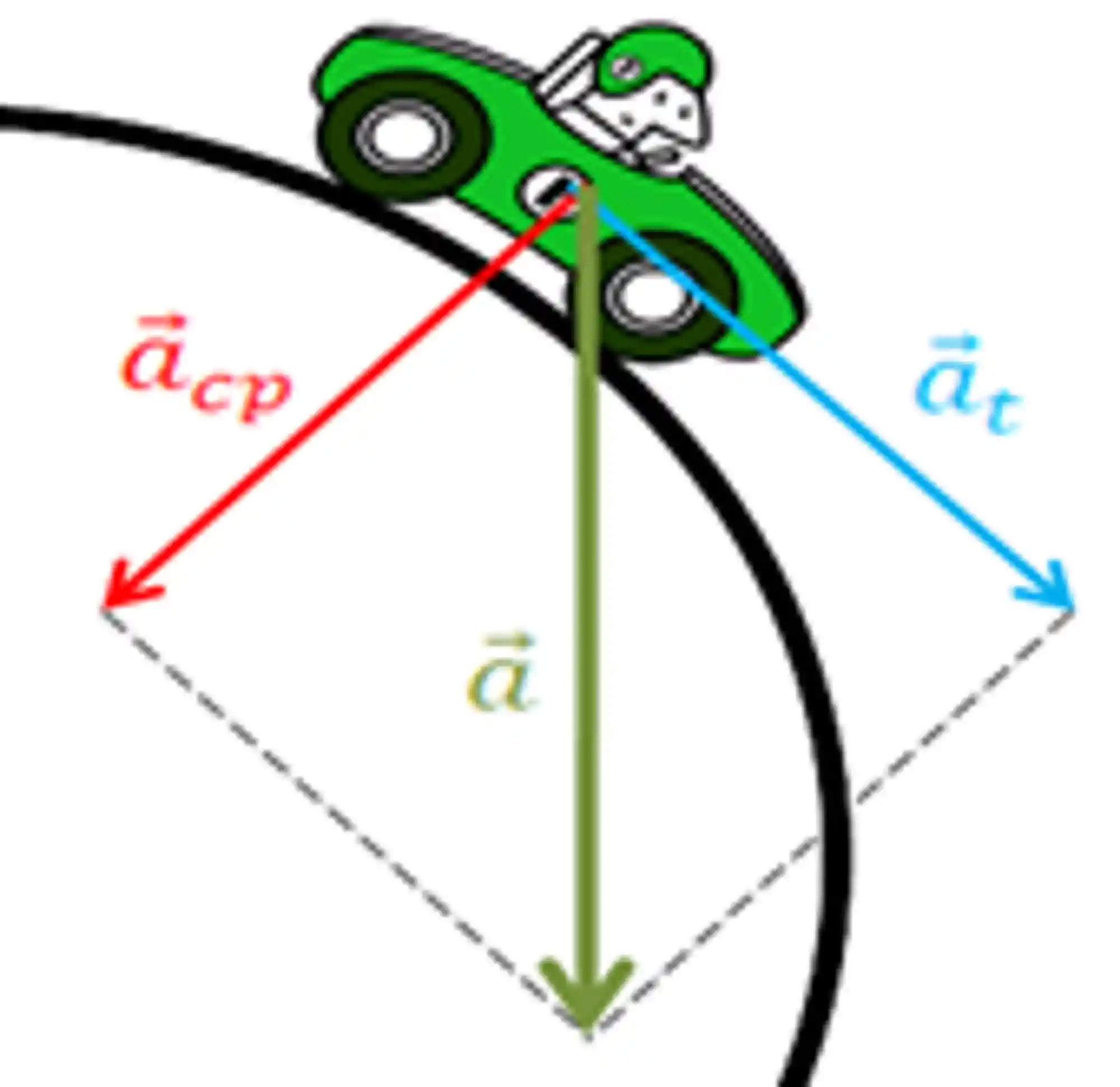
MCUV: Exemplo
MCUV: Exemplo

Considere que inicialmente a velocidade tangencial do carrinho acima é e ele tem uma aceleração tangencial igual a . Qual é a aceleração centrípeta e o módulo do vetor aceleração inicial, se o raio da trajetória é metros? Qual é o módulo do vetor aceleração depois de segundos? Qual é a distância que o carrinho percorreu depois desse tempo?

SIM, MUITAS PERGUNTAS! 😱 Eu sei, mas calma que a gente vai destrinchar coisinha por coisinha! Bora lá?

Aceleração Centrípeta

A aceleração centrípeta é a responsável por mudar a direção da velocidade, ou seja é por causa dela que o carrinho vai conseguir fazer a curva! Ela pode ser calculada usando a seguinte fórmula:

Onde é a velocidade tangencial e é o raio da trajetória. Para o nosso exemplo temos uma velocidade tangencial igual a e um raio igual a , então a nossa aceleração centrípeta no momento inicial vai ser igual a:

Uma coisa já foi, agora vamos pra próxima!

Aceleração Tangencial

A aceleração tangencial é a aceleração responsável pela mudança de velocidade escalar. Podemos calcula-la usando a seguinte fórmula:

Onde é a variação de velocidade quando a variação de tempo tende a zero! É importante saber que a aceleração tangencial SEMPRE possui direção paralela à direção do vetor velocidade.

Quando a aceleração tangencial está no mesmo sentido, a velocidade escalar aumenta e quanto a aceleração tangencial está em sentido contrário, a velocidade escalar diminui. No nosso exemplo a aceleração tangencial foi dada, seria interessante calcularmos a velocidade tangencial final pra avaliar o que acontece com o vetor aceleração depois de 5 segundos.

Aqui vai uma dica, se o exemplo te der as funções o jeito é resolver usando as derivadas mas no nosso caso com valores a gente pode dizer que:

Isolamos a velocidade final:

Substituindo os dados:

Aceleração Resultante

A aceleração resultante é a aceleração total do corpo. Ela é a soma vetorial da aceleração tangencial e da aceleração centrípeta, podemos representar na figura a resultante dessa forma:

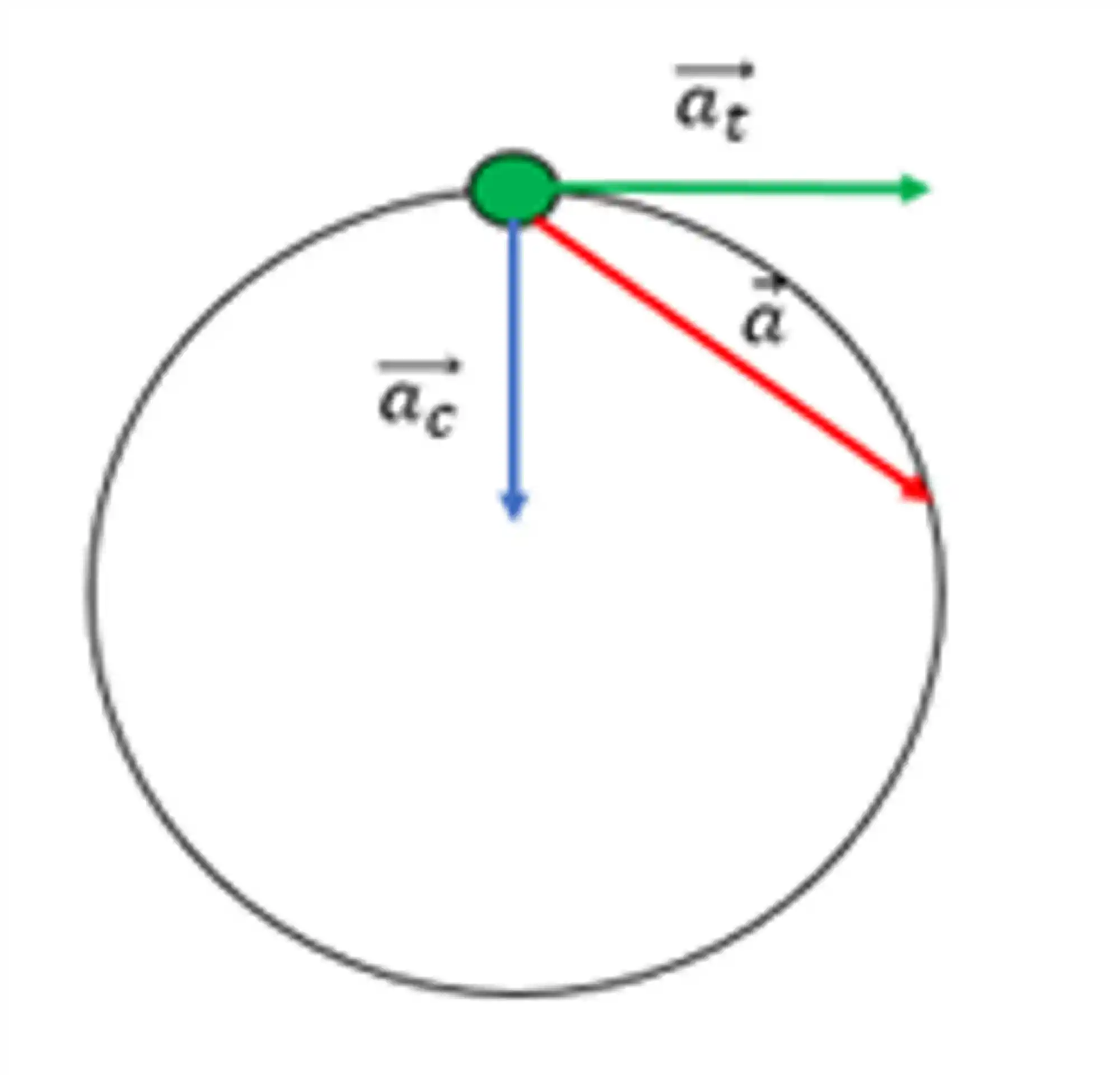
Aceleração resultante do MCUV
Aceleração resultante do MCUV

Para calcular o módulo da aceleração resultante, fazemos:

Para o nosso exemplo, no momento inicial temos:

Para o momento final precisamos calcular a aceleração centrípeta primeiro:

E finalmente:

Ou seja, no momento final ainda que a aceleração tangencial seja constante o vetor aceleração em si varia, por causa da aceleração centrípeta que muda.

Velocidade e Aceleração Angular

E o que vai acontecer com a velocidade angular? Ela é calculada do mesmo jeito, mas é diferente em cada ponto da trajetória já que depende da velocidade tangencial:

Vamos ver no nosso exemplo o módulo da velocidade angular inicial e a final:

Como a velocidade tangencial varia, a velocidade angular também vai sofrer variação
e a taxa dessa variação com o tempo é a aceleração angular! Então a gente pode escrever a aceleração angular da seguinte forma:

Posição Angular

E pra a gente quiser descobrir quanto andou o carrinho na trajetória após os segundos?

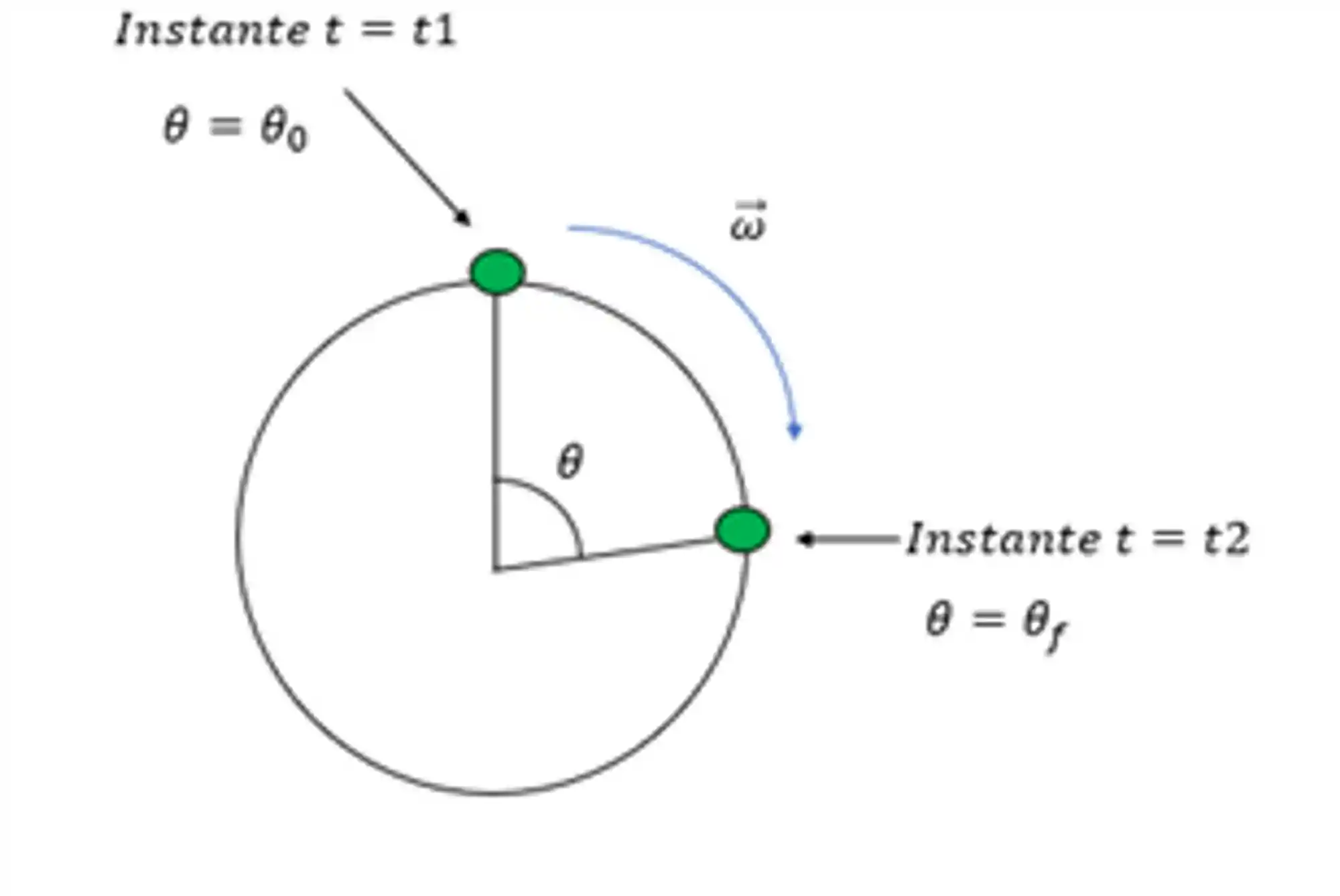
Posição Angular
Posição Angular

Aqui a gente não calcula em metros o quanto andou o carrinho mas sim quanto variou o ângulo da posição em relação ao centro da circunferência em radianos. Já te digo que podemos usar as equações do MRUV, porém trocando o espaço pelo ângulo e a velocidade pela velocidade angular, se liga:

²²

Agora vamos praticar com exercícios?!

Exercícios Resolvidos

Exercício Resolvido #1

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 83

A roda-gigante da figura abaixo, gira no sentido contrário ao dos ponteiros de um relógio. Em dado instante, um passageiro na periferia da roda e passando no ponto mais baixo do movimento circular se move a 3,00   m/s e está ganhando velocidade com uma taxa de 0,500   m/ s 2 . a) Determine o módulo, a direção e o sentido da aceleração do passageiro nesse instante. b) Faça um desenho do passageiro e da roda-gigante mostrando o vetor velocidade e o vetor aceleração.

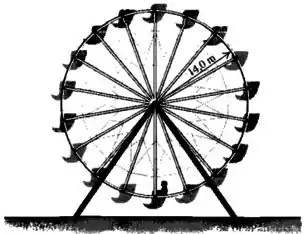
Passo 1

Pelo enunciado, considerando o movimento do passageiro, ele está em um movimento circular, e sua velocidade está aumentando.

Isso nós diz que neste caso temos aceleração centrípeta (movimento circular) e aceleração tangencial (aumento da velocidade).

Os dados do enunciado são

Dados v = 3   m / s a t = 0,5   m / s 2

Passo 2

a)

Para encontrarmos a aceleração total, primeiro vamos lembrar que ela é a soma vetorial da aceleração centrípeta com a aceleração tangencial.

Precisamos então calcular primeiro a aceleração centrípeta, usando a sua fórmula

a c p = v 2 R

a c p = 3 2 14 = 9 14   m/ s 2

Passo 3

Vamos fazer um esquema para mostrar o valor da aceleração total,

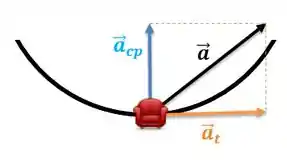
Temos cada componente

a c p = 9 14   m / s 2 a t = 0,5   m / s 2

Usando a fórmula de aceleração total,

a → 2 = a → c p 2 + a → t 2

a → 2 = 9 14 2 + 0,5 2

a → = a = 65 98   m/ s 2

Passo 4

b)

O esquema ficará

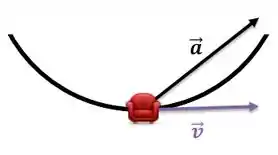
Resposta

  1. a → = a = 65 98   m/ s 2

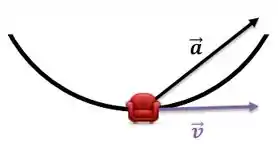
Exercício Resolvido #2

Elaboração Própria

No instante t = 0 , uma partícula parte com velocidade angular de 20 r a d / s em trajetória circular de raio 80 c m e sofre uma desaceleração de 2 r a d / s ² até parar. Determine:

  1. O número de voltas que ela realiza;
  2. O tempo de movimento;
  3. A aceleração tangencial.

Passo 1

Bora lá!

Aqui o problema é bem simples. A partícula está lá rodando na moral quando sofre uma desaceleração até parar. Isso nos lembra de um problema de MRUV, só que aqui ao invés de deslocamento linear teremos o angular.

Passo 2

a)

Sabendo disso, podemos utilizar a relação de Torricelli pra ângulos, já que temos a velocidade angular inicial, a velocidade angular final, a aceleração angular e o ∆ θ . Daí, teremos:

ω ² = ω 0 2 + 2 α ∆ θ

Como aqui temos ω 0 = 20 r a d / s , ω = 0 ,   e α = - 2 r a d / s ² .

Substituindo ali, teremos:

20 2 = 2.2 . ∆ θ

400 = 4 ∆ θ

∆ θ = 100 r a d

Como em uma volta, temos 2 π   r a d , fazendo regra de três, teremos:

1 v o l t a - - - - - - 2 π   r a d

n   v o l t a s - - - - - 100   r a d

n = 50 π   v o l t a s

Passo 3

b)

Utilizando agora a equação de Movimento Circular Uniformemente Acelerado que utiliza o tempo, teremos:

θ = θ 0 + ω 0 t + α t 2 2

100 = 0 + 20 t - t ²

Opa, encontramos uma equação do 2° grau. Agora é só usar Bháskara e correr pro abraço. Vamos lá!

t 2 - 20 t + 100 = 0

∆ = 20 2 - 4.1 . 100 = 0

Como ∆ = 0 a gente só vai ter uma raiz, então...

t = - b ± ∆ 2 a = 20 2 = 10 s

Meio chato ter que fazer Bháskara, né? Podemos também resolver de uma forma mais simples usando essa fórmula:

ω = ω 0 + α t

Como ω 0 = 20 r a d / s , ω = 0 ,   e α = - 2 r a d / s ² :

0 = 20 - 2 t

t = 10   s

Passo 4

c)

Ah, aqui é bem mais simples!

Lembra lá, a aceleração tangencial é calculada por

a t g = α R

a t g = - 2.0,8 = - 1,6 m / s ²

E é isso aí!

Resposta

a) n = 50 π   v o l t a s

b) t = 10 s

c) a t g = - 1,6 m / s ²

Exercício Resolvido #3

Brasil Escola

O gráfico a seguir representa a velocidade angular, em função do tempo, de uma polia que gira ao redor de um eixo.

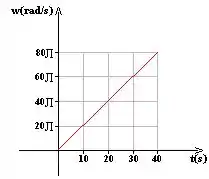
Com base nas informações contidas no gráfico, determine a aceleração angular desta polia e a quantidade de volta que ela dá no intervalo de tempo entre 0 e 40s.

Passo 1

Bom, pra gente calcular a aceleração angular tendo a velocidade angular inicial, final e o tempo, podemos usar a equação da velocidade no movimento circular acelerado! Então:

ω = ω 0 ±   α t

Onde α é a aceleração angular que queremos descobrir! Show! Então vamos usar os dados que a questão nos deu:

80 π = 0 ±   α . 40

α = 2 π   r a d / s 2

Lindíssimo!

Passo 2

Agora que temos a aceleração angular, fica fácil descobrirmos o espaço total percorrido, né?

Vamo lá, nossa equação é:

θ =   θ 0 ± ω 0 t ± α t 2 2

∆ θ = ω 0 t ± α t 2 2

Então, temos:

∆ θ = 0.40 ± 2 π ( 40 ) 2 2

∆ θ = 1600 π   r a d

Showww!

Passo 3

Bom, agora pra finalizarmos, a questão nos pediu o número de voltas, como uma volta vale 2 π   r a d , é só dividirmos ∆ θ por esse valor! Simbora:

1600 π r a d 2 π r a d = 800   v o l t a s    

Resposta

α = 2 π   r a d / s 2 e 800   v o l t a s

Exercício Resolvido #4

Elaboração Própria

A aceleração de um corpo faz um ângulo de π / 6   r a d com a tangente do movimento, como mostrado na figura abaixo. Determine a equação que relaciona a velocidade angular e a aceleração angular.

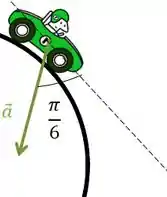
Passo 1

Nós sabemos que a aceleração tangencial pode ser relacionada com a aceleração angular.

a t = α R

E a aceleração centrípeta é

a c p = v 2 R

Mas queremos a velocidade angular e não a escalar, lembrando que

v = ω R

E substituindo na equação pra aceleração centrípeta, fica

a c p = ω R 2 R = ω 2 R

Tá mas e agora?

Passo 2

Como ele deu o ângulo podemos faz as componentes da aceleração, uma tangencial e outra apontando para o centro da curva, no caso a centrípeta.

Vamos usar a “regra COlado/SEparado”

a t = a ⋅ cos ⁡ π 6 = 3 2 a

a c p = a ⋅ sen ⁡ π 6 = 1 2 a = a 2

Passo 3

Beleza, mas e agora?

Dividindo a aceleração tangencial pela centrípeta que temos no passo 1 vamos encontrar

a t a c p = α R ω 2 R = α ω 2

Agora fazendo a mesma coisa só que com as equações do passo 2

a t a c p = 3 2 a a 2 = 3

Podemos igualar esses dois resultados

α ω 2 = 3

E pronto temos uma relação entre os dois.

Resposta

α ω 2 = 3

Exercício Resolvido #5

SoFísica

Um volante circular como raio 0,4 metros gira, partindo do repouso, com aceleração angular igual a 2rad/s².

a) Qual será a sua velocidade angular depois de 10 segundos?

b) Qual será o ângulo descrito neste tempo?

c) Qual será o módulo vetor aceleração resultante?

Passo 1

Fala aí! Vamo nessa?

Pela função horária da velocidade angular, temos:

ω = ω 0 + α . t

Como a questão nos diz que o volante parte do repouso, nossa velocidade inicial é 0. Temos a aceleração angular e o tempo, é só subtituir na fórmula!

ω = 0 + 2.10

ω = 20 r a d / s

Prontinho! A letra a já foi!

Passo 2

Pela função horária do deslocamento angular, a gente tem que:

φ = φ 0 + ω 0 t + α t 2 2

Como temos todos os dados, temos:

∆ φ = ω 0 t + α t 2 2

∆ φ = 0.10 + 2 . 10 2 2

∆ φ = 100 r a d

Mais uma letrinha prontaaa!

Passo 3

Pelas relações de aceleração tangencial e centrípeta que conhecemos, temos:

a t a n g e n c i a l = α R

a t a n g e n c i a l = 2.0,4 = 0,8 m / s 2

a c e n t r í p e t a =   ω 2 R

a c e n t r í p e t a =   20 2 . 0,4 = 160 m / s 2

Showw! Então temos as duas componentes da aceleração resultante, pra calcularmos o módulo desse vetor é só usarmos aquela regrinha que já vimos infinitas vezes:

a t o t a l = √ ( a t a n g e n c i a l 2 + a c e n t r í p e t a 2 )

a t o t a l = 160,002 m / s 2

Então só pra deixar bem fixado na tua cabeça, é assim que ficam as velocidades representadas vetorialmente:

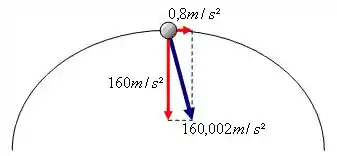
Conseguimos!

Resposta

  1. ω = 20 r a d / s
  2. ∆ φ = 100 r a d
  3. a t o t a l = 160,002 m / s 2

Exercício Resolvido #6

UFPE 2015.1 3ºEE

A posição angular de um ponto da borda de uma roda que gira em torno de seu centro é dada por θ t = π t 3 + 3 t 2 + 2 t , onde θ está em radianos e t em segundos.

Quantas voltas tal ponto dá em torno do centro da trajetória circular entre os instantes t = 0   s e t = 4   s ?

  1. 12
  2. 24
  3. 16
  4. 48
  5. 120
  6. 60

Passo 1

Bora pra mais uma?

O ponto da borda vai girando ao redor do centro numa trajetória circular, sendo que sua posição angular é dada pela função:

θ t = π t 3 + 3 t 2 + 2 t

No tempo t = 0 , nós temos θ = 0 . Agora, depois disso, quantas voltas ela dá?

Vamos pensar em geometria um pouco. Uma volta ao redor de uma circunferência corresponde a um ângulo de 2 π   r a d . Se você der n voltas, você tem:

θ = n ∙ 2 π = 2 n π

n = 0 ,   1 ,   2 ,   3 ,   …

Agora, calculando a posição angular dele no tempo t = 4   s .

θ t = 4 s = π 4 3 + 3 ∙ 4 2 + 2 ∙ 4

θ t = 4 s = π 64 + 48 + 8 = 120 π

Para vermos a quantas voltas isso corresponde, nós igualamos com a fórmula para n voltas.

120 π = 2 n π

n = 60   v o l t a s

Showww!

Resposta

f )     60

Exercício Resolvido #7

USP 2013.1

Um DJ, ao preparar seu equipamento, esquece uma caixa de fósforos sobre o disco de vinil, em um toca-discos desligado. A caixa se encontra a 10 cm do centro do disco. Quando o toca-discos é ligado, no instante t = 0, ele passa a girar com aceleração angular constante α = 1,1 rad/ s 2 , até que o disco atinja a frequência final f = 33 rpm que permanece constante. O coeficiente de atrito estático entre a caixa de fósforos e o disco é μe = 0,09. Determine:a) a velocidade angular final do disco, ω f , em rad/sb) o instante t f em que o disco atinge a velocidade angular ω f c) a velocidade angular ω c do disco no instante t c em que a caixa de fósforos passa a se deslocar em relação ao mesmoNote e adote:Aceleração da gravidade local g =10 m/s2.π = 3

Passo 1

Simboraa? Como a questão nos deu a frequência final, podemos usar, como gente já viu antes, essa formulinha pra encontrar a velocidade angular final:

ω f = 2лf

Mas como nossa frequência tá em rpm, devemos dividir por 60 pra encontrarmos em Hz, porque a resposta se pede em rad/s. Show!

ω f = 2лf = 2 . 3 . 33/60 rad/s ω f = 3,3 rad/s

Prontoo! A primeira parte já foi.

Passo 2

Como a questão nos disse que a aceleração angular é constante, então podemos usar nossa função horária da velocidade no Movimento Circular Acelerado, então:

ω = ω₀ + α.t3,3 = 0 + 1,1. t f

t f = 3 s

Passo 3

Essa é mais complicadinha, né? Mas bora lá! Vamo pensar na lógica, se você colocar uma caixinha em cima de algo que ta girando cada vez mais rápido, essa caixinha tende a cair, ou seja, terá uma força atuando nela apontando pra fora do círculo, que, no nosso caso, é a força de atrito! E como temos a força centrípeta apontando pro meio do círculo, temos pelo equilíbrio de forças que:

F a t = F c p

N . μ = m ω 2 r

Como não temos nenhuma força atuando no sentido da força peso além da normal, temos que:

N = P = m g

Prontinho! Então vamos substituir isso lá em cima:

N . μ = m ω 2 r

m g . μ = m ω 2 r

g . μ = ω 2 r

ω = g μ r = 0,09.10 0,10 = 3 r a d / s

Conseguimos!

Resposta

a)   ω f = 3,3 rad/s

b) t f = 3 s

c) ω = 3 r a d / s

Exercício Resolvido #8

UFPE 2013.1 3ºEE

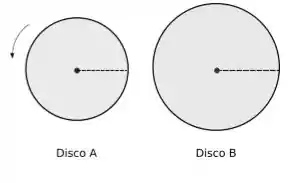
A figura mostra dois discos que podem girar em torno de seus centros independentemente. No instante t   =   0 , as retas de referência dos dois discos têm a mesma orientação (como mostrado no desenho); o disco A já está girando com uma velocidade angular constante ω A = 3 π   r a d / s e o disco B parte do repouso com uma aceleração angular constante de 0,5 π   r a d / s 2 .

a) Em que instante t as duas retas de referência têm o mesmo deslocamento angular θ ?

b) Qual será o primeiro instante t , após t   =   0 , para o qual as duas retas de referência estão paralelas com a linha que une o centro dos dois discos?

c) Considere agora que o deslocamento angular do disco B varia no tempo com θ B t = t 3 - 2 t , onde θ B ( t ) está em radianos. Em qual instante a velocidade angular de B é igual à velocidade angular de A ?

Passo 1

Fala aí! Bom, os deslocamentos angulares dos discos são:

θ A = 3 π t

θ B = 0,5 π t 2 2

Como elas tem o mesmo deslocamento, igualando os dois, temos:

3 π t = 0,5 π t 2 2 → t = 12   s  

Já foi uma parte!

Passo 2

A sacada aqui é perceber que as retas de referência estarão alinhadas quando os deslocamentos forem separadamente múltiplos de π ou 2 π . Sacou?

Na real, podemos dizer que os deslocamentos serão múltiplos (distintos) de π , já que serão também múltiplos de 2 π , né?

Para o disco A , é necessário que:

θ A = 3 π t = π n

Portanto:

t = n 3

Então, isso significa que:

θ B = π t 2 4 = π n 2 4   .   9

Com isso, concluímos que, se:

n = 6 m

Teríamos:

θ A = π n e θ B = π m 2

Viu que para qualquer m e n eles serão múltiplos de π ? Portanto, a primeira vez que se encontram é quando m = 1 , n = 6 e então t = 6 3 = 2   s

Passo 3

Para obter a velocidade angular, é só derivar a posição!

ω B = d θ B t d t = d d t t 3 - 2 t = 3 t 2 - 2

Assim, ω B = ω A implica em:

3 t 2 - 2 = 3 π

E então:

t = 2 3 + π   s

Resposta

a) t = 12   s

b) t = 2   s

c) t = 2 3 + π   s

Exercícios de Livros Relacionados

O volante de uma máquina a vapor gira com uma velocidade angular constante de 150r e v / m i n . Quando a máquina é desligada, o atrito dos mancais e a resistência do ar param a roda em2,2h . (a) Qual
O prato de um toca-discos está girando a 33 1 3r e v / m i n . Uma semente de melancia está sobre o prato a 6,0c m de distância do eixo de rotação. (a) Calcule a aceleração da semente, supondo que ela
Na Figura 9.38 , o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui um
Um roda começa a girar a partir do repouso em t= 0 com aceleração angular constante. No instante t=2,0s , a velocidade angular da roda é 5,0r a d / s . A aceleração cessa abruptamente no instante t=20
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c