Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Movimento Circular Uniforme (MCU)

Ver Todos os Exercícios

Teoria

No movimento circular uniforme (MCU) um objeto se move em velocidade escalar constante ao longo de uma trajetória circular, repetidamente, sempre em um mesmo intervalo de tempo.

-Quee?! 😖

Calma, a gente já vai aprender timtim por timtim! Mas pra começar com o pé direito, confere esse vídeo que o Responde Aí preparou pra você aprender tudo o que você precisa sobre Movimento Uniforme 👇

📢Clique para ver mais:

Quando estamos falando de movimento circular uniforme a gente precisa ter em mente alguns conceitos MUITO importantes!

Bora aprender eles?! 👇

Aceleração Centrípeta

Ué, mas a gente tá falando de movimento circular UNIFORME, como assim aceleração?!

Calma, a aceleração centrípeta é incapaz de mudar o módulo da velocidade! Ela é uma componente da aceleração perpendicular à trajetória e ela é responsável pela mudança de direção!

Ela pode ser calculado usando a seguinte fórmula:

Onde, é a velocidade escalar e é o raio do movimento circular!

Período e Frequência


O período é o tempo que uma partícula leva para fazer uma volta completa. No intervalo , a partícula se desloca a uma distância igual ao comprimento da circunferência, ou seja . =)


Como no o módulo da velocidade é constante durante a volta percorrida pela partícula, podemos relacionar a velocidade escalar com a distância percorrida em uma volta e o tempo de percurso.

Assim:

Podemos substituir a velocidade na fórmula de aceleração centrípeta:

Chegamos a:

Agora, a frequência é o número de voltas dadas em um intervalo de tempo. Ou seja, ela é igual ao inverso do período.

A gente também pode escrever a velocidade em função da frequência.

Deslocamento Angular

Quando realizamos um movimento circular, realizamos uma alteração no valor do ângulo. Essa alteração pode ser chamada de deslocamento angular.

Se liga no Dexter girando 🤣🤣🤣

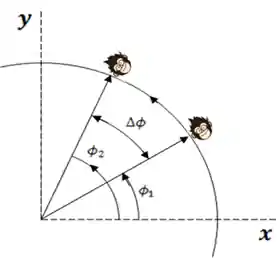
Movimento angular do Dexter
Movimento angular do Dexter

Repare que o nosso mascote está inicialmente em um ângulo em relação ao eixo . Ele faz a curva e passa a fazer um ângulo com o eixo .

Ele variou seu ângulo, certo? Essa variação que é o deslocamento angular.

Numa curva, ao manter o raio constante, podemos ter uma relação do deslocamento angular com a distância percorrida!

Pra calcular o deslocamento angular, fazemos:

Velocidade Angular

A velocidade angular é a variação do deslocamento angular pelo tempo. Se o ângulo varia muito rápido, podemos dizer que ele tem uma velocidade angular alta.

Para calcularmos a velocidade angular média basta fazer a divisão da variação total de deslocamento angular pelo tempo total do movimento .

Para uma volta completa, podemos escrever:

Agora, vamos praticar com exercícios?!

Aceleração Centrípeta

Período e Frequência

Deslocamento Angular

Velocidade Angular

Exercícios Resolvidos

Exercício Resolvido #1

Mundo Educação

Um corredor mantém em uma pista circular uma velocidade constante de 2m/s e completa uma volta em 80 s. Determine a frequência de giro do corredor e o tamanho da pista circular.

a) 0,00150 Hz e 180 m

b) 0,0125 Hz e 170 m

c) 0,0125 Hz e 160 m

d) 0,0325 Hz e 180 m

e) 0,0525 Hz e 160 m

Passo 1

E aí! Vamo nessa? A sacada aqui é percebermos que p tempo de 80s corresponde exatamente ao período de rotação do corredor. Sabendo que a frequência é o inverso do período, temos:

f = 1 T = 1 80 = 0,0125 H z

A primeira parte já foi! Hehe

Passo 2

Como a nossa velocidade é constante, podemos usar as equações do movimento uniforme aqui, né? Então vamos lembrar:

v = ∆ S ∆ t

Nós temos a velocidade e temos o tempo, que foram nos dados na questão! Agora é só substituirmos e encontrarmos o espaço ∆ S , que é exatamente o tamanho da pista circular!

v = ∆ S ∆ t   → 2 = ∆ S 80

∆ S = 160 m

Fechamos!!

Resposta

c) 0,0125 Hz e 160 m

Exercício Resolvido #2

UNICAMP

Anemômetros são instrumentos usados para medir a velocidade do vento. A sua construção mais conhecida é a proposta por Robinson em 1846, que consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme figura abaixo. Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela velocidade linear das conchas. Um anemômetro em que a distância entre as conchas e o centro de rotação é r=25 cm, em um dia cuja velocidade do vento é v=18 km/h, teria uma frequência de rotação aproximadamente de

Se necessário, considere π = 3.

a) 3 rpm.

b) 200 rpm.

c) 720rpm.

d) 1200 rpm.

Passo 1

Pra resolver essa questão aqui a gente pode usar a relação entre velocidade linear e velocidade angular, né? A gente sabe que:

v = ω r

Mas também sabemos que a velocidade angular pode ser calculada assim:

ω = 2 π f

Então, substituindo na primeira equação temos que:

v = ω r → v = 2 π f r

Show, né? Agora temos todos os dados pra encontrarmos a frequência! Mas nossa velocidade foi dada em km e o raio dado em cm... Vamos passar tudo pra metro pra ficar mais bonitinho e em unidades iguais! Para transformarmos de km/h para m/s é só dividirmos por 3,6, então:

18 3,6 = 5 m / s

Show! E o nosso raio que vale 25cm vale 0,25m. Agora vamos substituir!

v = 2 π f r

5 = 2.3 . f . 0,25   → f = 5 1,5 = 3,33 H z

Show! Terminamos! MAS PERAÊ! A questão quer a frequência em rpm. Como Hz é a unidade de frequência pra segundos, devemos multiplicar 3,33 por 60 pra encontrarmos em minutos!

3,33 x 60 = 199,8 r p m   ≅ 200 r p m

Conseguimos! Agora acabamos! :D

Resposta

b) 200 rpm.

Exercício Resolvido #3

FUVEST

Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a 100 m, como ilustra a figura abaixo. Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante ω. As pessoas terão sensação de peso, como se estivessem na Terra, se a velocidade ω for de, aproximadamente,

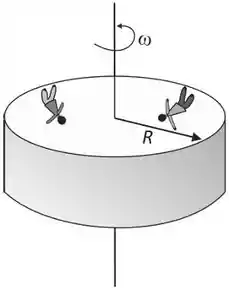
a) 0,1 rad/s

b) 0,3 rad/s

c) 1 rad/s

d) 3 rad/s

e) 10 rad/s

Note e adote:

A aceleração gravitacional na superfície da Terra é g = 10 m/s2

Passo 1

Nesse problema o enunciado diz que a estação gira para simular o efeito gravitacional. Esse giro do cilindro vai gerar uma aceleração centrípeta e com ela uma força centrípeta, isso acontece na superfície terrestre também, onde a força centrípeta é igual ao peso do corpo.

Se liga da imagem onde o pontinho verde representa uma pessoa em cada ponto do cilindro com sua aceleração centrípeta a c e velocidade tangencial v T :

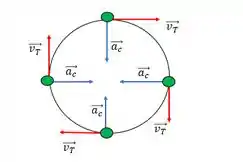
Pela segunda lei de newton temos o seguinte

F c p = m a c = m v T 2 R

Podemos então representar essa força no sentido da aceleração:

Passo 2

Como foi falado no passo 1, a força centrípeta que mantem a gente preso no movimento de rotação na terra é igual ao peso do corpo, e queremos com a rotação simular isso aqui, então faremos:

F c p = P

m v T 2 R = m g

Cortando as massas dos dois lados temos:

v T 2 R = g

Mas, como queremos saber da velocidade angular, devemos lembrar que:

v T = ω R

Entããão, temos:

ω 2 R = g

Como queremos a velocidade angular para qual a sensação de peso será igual a da terra, temos que a gravidade vale 10m/s2

Substituindo todos os dados na equação, temos que:

ω 2 100 = 10

ω 2 = 0,1   → ω = 0,1 ≅ 0,3 r a d / s

Show! Conseguimos!

Resposta

b) 0,3 rad/s

Exercício Resolvido #4

UNICAMP

Considere um computador que armazena informações em um disco rígido que gira a uma frequência de 120 Hz. Cada unidade de informação ocupa um comprimento físico de 0,2μm na direção do movimento de rotação do disco. Quantas informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver posicionada a 3 cm do centro de seu eixo, como mostra o esquema simplificado apresentado abaixo? (Considere π ≈ 3.)

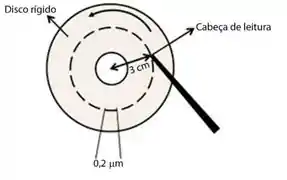
a)  1,62 ⋅ 10 6

b)  1,8 ⋅ 10 6

c)  64,8 ⋅ 10 8

d)  1,08 ⋅ 10 8

Passo 1

A gente precisa encontrar o número X de informações magnéticas que passam por segundo pela cabeça de leitura do disco rígido. Pra fazer isso a gente vai primeiro encontrar a velocidade angular

Usando a relação de velocidade linear com velocidade angular, temos:

v = ω R

Mas podemos calcular a velocidade angular ω também, né? Usando que:

ω = 2 π f

Substituindo os valores na equação temos:

ω = 2 π × 120 = 240 π r a d / s

Passo 2

Para encontrarmos a distância percorrida nessa velocidade em 1 segundo, é só usarmos a formulinha de velocidade angular constante:

ω = ∆ θ ∆ t

240 π = ∆ θ 1

∆ θ = 240 π r a d

E agora pra encontrar o espaço percorrido é só a gente fazer:

∆ S = ∆ θ R

Onde R é a distância entre o centro do disco e a cabeça de leitura e vale 3 c m = 0,03 m . Assim temos, aproximando π = 3 como recomenda o enunciado.

∆ S = 240 × 3 × 0,03 = 0,188 = 21,6 c m

Sabemos que uma unidade de informação magnética que chamaremos de U ocupa 0,2 μ m , vamos converter esse comprimento para metros fazendo:

1 μ m = 10 - 6 m

Assim uma unidade de informação U ocupa um espaço de   0,2 x 10 - 6 m , como temos ∆ S = 21,6 m , só usarmos uma regrinha de três! Então temos:

21,6 m → X   U

0,2 x 10 - 6 m → 1   U                    

X = 21,6 0,2 × 10 - 6 U = 1,08 x 10 8 U

Portanto, em um segundo, passam 1,08 × 10 8 unidade de informações magnéticas pelo equipamento de leitura.

Showww!

Resposta

d)  1,08 ⋅ 10 8

Exercício Resolvido #5

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 88. 57

Em uma parque de diversões uma mulher passeia em uma roda-gigante com 15 m de raio, completando 5 voltas em torno do eixo horizontal a cada minuto. Quais são:

  1. O período do movimento?
  2. O módulo da aceleração centrípeta no ponto mais alto?
  3. O sentido da aceleração centrípeta no ponto mais alto?
  4. O módulo da aceleração centrípeta no ponto mais baixo?
  5. O sentido da aceleração centrípeta no ponto mais baixo?

Passo 1

  1. Sabendo que período é o inverso da frequência, vamos aplicar a fórmula:

T = 1 f

A frequência é o número de voltas dadas em um determinado tempo:

f = 5 1 m i n = 5 60 s = 1 12 s

Logo, o período é:

T = 12 s 1 = 12 s

Passo 2

b) Vamos utilizar a fórmula de aceleração centrípeta: | a → c p | = v 2 R

Mas, como a velocidade não é dada, precisamos descobri-la.

O tempo para uma volta completa é o período e vale 12s. O deslocamento é o comprimento do círculo e vale 2 π R .

Então, ∆ t = 12 s   e ∆ s = 30 π

v = ∆ s ∆ t = 30 π 12 = 7.85 m s

Agora que achamos a velocidade, podemos substituir na fórmula de aceleração centrípeta.

| a → c p | = 7,85 2 15 = 4.1 m s 2

Passo 3

c) A aceleração centrípeta sempre tem direção radial, ou seja, em direção ao centro do círculo. No caso, no ponto mais alto, o sentido é para baixo ou – j .

Passo 4

d) A aceleração centrípeta não vai depender do ponto escolhido. Ela é calculada da mesma forma do item b) e vale 4.1 m / s ² = 4 m / s ² .

Passo 5

e) A aceleração centrípeta sempre tem direção radial, ou seja, em direção ao centro do círculo. No caso, no ponto mais baixo, o sentido é para cima ou + j .

Resposta

  1. 12s
  2. 4.1m/s²
  3. Baixo
  4. 4.1m/s²
  5. Cima

Exercício Resolvido #6

Elaboração Própria

Um helicóptero que está se preparando para decolar, liga suas hélices. Nesse momento a hélice possui velocidade constante, realizando uma volta completa em 0,004   s . Determine a velocidade angular das pás do helicóptero e o deslocamento em cada ponto marcado em vermelho, mostrado no desenho abaixo, após 4 segundos.

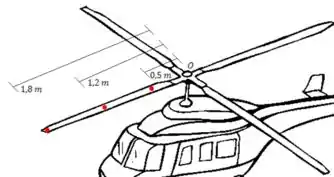
Passo 1

Vamos começar achando a velocidade angular, como a velocidade é constante a velocidade angular deve ser constante também. A fórmula da velocidade angular é

ω = Δ θ Δ t

Ele deu o tempo que ele demora para dar uma volta, isso quer dizer que

Δ θ = 2 π

E o período do movimento é

T = 0,004 s

Resultando em

ω = 2 π T = 2 π 0,004

ω = 500 π   rad / s

A unidade de velocidade deve ser sempre em radianos por segundo. Cuidado que o ângulo deve estar em radianos, e não em grau.

Passo 2

Como a velocidade angular é constante, podemos descobrir o deslocamento angular multiplicando a velocidade pelo tempo total do movimento que é Δ t = 4 s .

Δ θ = Δ t ⋅ ω

Δ θ = 4 ⋅ 500 π = 2000 π   rad

O deslocamento pode ser relacionado com o deslocamento angular com

Δ S = Δ θ ⋅ R

Então

Δ S = 2000 π R

Passo 3

Vamos fazer essa conta para cada ponto

R 1 = 0,5   m

Δ S 1 = 2000 π ⋅ 0,5 = 1000 π   m

R 2 = 1,2   m

Δ S 2 = 2000 π ⋅ 1,2 = 2400 π   m

R 3 = 1,8   m

Δ S 3 = 2000 π ⋅ 1,8 = 3600 π   m

Resposta

ω = 500 π   rad / s

Δ S 1 = 1000 π   m

Δ S 2 = 2400 π   m

Δ S 3 = 3600 π   m

Exercício Resolvido #7

UNICAMP, Física 1, Prova 1, 2015.1

Uma partícula descreve um movimento circular uniforme de raio R em um plano horizontal, em um sistema de coordenadas onde a origem se encontra no centro da circunferência. Qual destas afirmações é falsa:

  1. A velocidade média depois de um período completo é nula
  2. A velocidade escalar média depois de um período T completo é igual a 2 π R T
  3. O produto escalar entre o vetor velocidade e o vetor posição da partícula é sempre nulo.
  4. O produto escalar entre o vetor velocidade e o vetor aceleração da partícula é sempre nulo.
  5. O produto escalar entre o vetor aceleração e o vetor posição da partícula é sempre nulo.

Passo 1

Vamos analisar as alternativas uma a uma.

Alternativa (a) – Verdadeira.

A velocidade média a que o enunciado se refere é o vetor velocidade média que tem a fórmula:

v → m e d = Δ S → Δ t

Portanto, após um ciclo completo, o deslocamento vetorial Δ S → é nulo, pois o ponto inicial e final do vetor são os mesmos. Então a velocidade média vetorial também será nula.

Passo 2

Alternativa (b) – Verdadeira.

O deslocamento escalar total é o comprimento do círculo, ou seja, 2 π R . Então após um período completo T, teremos:

v m e d = 2 π R T

Passo 3

Alternativa (c) – Verdadeira.

Estando a origem do sistema de coordenadas no centro da trajetória circular, o vetor posição é sempre radial e perpendicular ao vetor velocidade instantânea, que é sempre tangencial à trajetória;

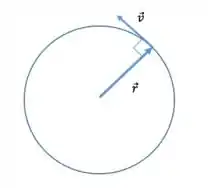
Passo 4

Alternativa (d) – Verdadeira.

Como o movimento é uniforme, não possui aceleração tangencial, apenas aceleração centrípeta. Logo, o vetor aceleração é radial, assim como o vetor posição. É, portanto, perpendicular ao vetor velocidade instantânea em todos os momentos.

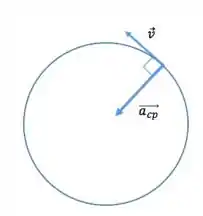
Passo 5

Alternativa (e) – Falsa.

Os vetores aceleração e posição apontam na mesma direção, mas em sentidos opostos. O único jeito do produto escalar ser nulo é se um dos vetores for nulo ou se eles forem perpendiculares. Como isso não ocorre, essa afirmativa é falsa.

Resposta

Letra (e)

Exercício Resolvido #8

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 88. 4- 63.

Uma bolsa a 2,00   m do centro e uma carteira a 3,00   m do centro descrevem um movimento circular uniforme no piso de um carrossel. Elas estão na mesma linha radial. Em um certo instante, a aceleração da bolsa é ( 2,00   m / s ² ) i   +   ( 4,00   m / s ² ) j . Qual é a aceleração da carteira nesse instante, em termos dos vetores unitários.

Passo 1

Ele nos dá uma aceleração aí e nos diz que o movimento é circular uniforme. O que isso quer dizer?

Tudo! Movimento circular uniforme só tem aceleração centrípeta, então essa aceleração aí é a centrípeta

Vamos desenhar um esqueminha nesse do que está acontecendo nesse nosso carrossel verde abaixo, com a bolsa na cor preta e a carteira na cor roxa.

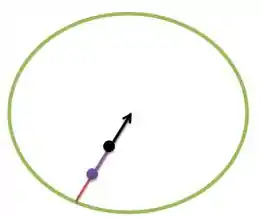
Passo 2

Sabemos que o módulo da aceleração centrípeta pode ser calculada por:

a → c p = v 2 R

Mas para só pra pensar, se eles estão em cima do carrossel , eles estão sob mesma velocidade angular, pois a variação do ângulo num mesmo intervalo de tempo vai ser igual pra todos.

Sabemos também que v = ω R e substituindo ali, teremos:

a → c p = ω ² R

Passo 3

Escrevendo a aceleração de cada uma, teremos:

a → c p b o l s a = ω ² . 2

a → c p c a r t e i r a = ω ² . 3

Dividindo uma pela outra, teremos:

a → c p b o l s a a → c p c a r t e i r a = ω ² . 2 ω ² . 3

E assim, teremos:

3 2 a → c p b o l s a = a → c p c a r t e i r a

Passo 4

Beleza, mas quem é a → c p b o l s a ? É justamente o módulo do vetor a → c p b o l s a = ( 2,00   m / s ² ) i   +   ( 4,00   m / s ² ) j

Como calcula? Fácil!

a → c p b o l s a = 2 ² + 4 ² = 20 = 2 5

Assim, a → c p c a r t e i r a será:

a → c p c a r t e i r a = 3 2 a → c p b o l s a = 3 2 . 2 5 = 3 5

Passo 5

Beleza, já temos o módulo, mas queremos o vetor que representa a aceleração.

A gente sabe que ele deve apontar para a mesma direção que a → c p b o l s a , porém com módulo 3 5 . Pra achar esse vetor, temos que achar os vetores unitários que dão a direção para a aceleração da bolsa, pra fazer isto basta dividir o vetor pelo módulo do vetor.

a → u n i t a r i o = 1 2 5 .   2 m s 2 i ^   +   4 m s 2 j ^ =   1 5 m s 2 i ^   +   2 5 . m s 2 j ^

Daí

a → c p c a r t e i r a = a → c p c a r t e i r a x   a → u n i t a r i o

a → c p c a r t e i r a = 3 5 . 1 5 m s 2 i ^   +   2 5 . m s 2 j ^ =   ( 3 m / s ² ) î   +   ( 6 m / s ² ) j ^

Resposta

a → c p c a r t e i r a =   ( 3 m / s ² ) i ^   +   ( 6 m / s ² ) j ^

Exercícios de Livros Relacionados

Uma partícula P se move com velocidade escalar constante sobre uma circunferência de raio r=3,00m (Fig. 4 56) e completa uma revolução a cada 20,0s . A partícula passa pelo ponto O no instante t= 0 .
Um astronauta é posto em rotação em uma centrífuga horizontal com um raio de 5,0m . (a) Qual é a velocidade escalar do astronauta se a aceleração centrípeta tem um módulo de 7,0g ? (b) Quantas revoluç
Um carrossel de um parque de diversões gira em torno de um eixo vertical com velocidade angular constante. Um homem em pé na borda do carrossel tem uma velocidade escalar constante de 3,66m / s e uma
Uma bolsa a 2,00m do centro e uma carteira a 3,00m do centro descrevem um movimento circular uniforme no piso de um carrossel. Os dois objetos estão na mesma linha radial. Em um certo instante, a acel
75. Nos Problemas de 74 a 76 são fornecidas algumas equações que devem ser usadas para resolver um problema. Para cada um deles, você deve a. Escrever um problema realista para o qual estas equações s