Rolamento sem Deslizamento
Produzido por Ludovic BeghinTeoria
Opaaa! Partiu aprender TUDO sobre Rolamento sem Deslizamento com o RespondeAí?!
Vamo que vamo então! E pra começar com tudo vamos entender o que é Rolamento?
Se juntarmos os movimentos de translação e de rotação o que acontece?
Temos o movimento de rolamento. O exemplo mais simples que eu posso te dar é um roda rolando sobre uma superfície.
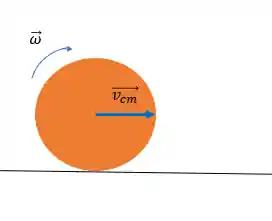
Tá, e o que tem de interessante nisso? No movimento de rotação cada ponto em uma roda de raio
Se o centro de massa dessa roda também translada com uma velocidade
Isso fica bem mais fácil de visualizar com essa figura esperta aqui:
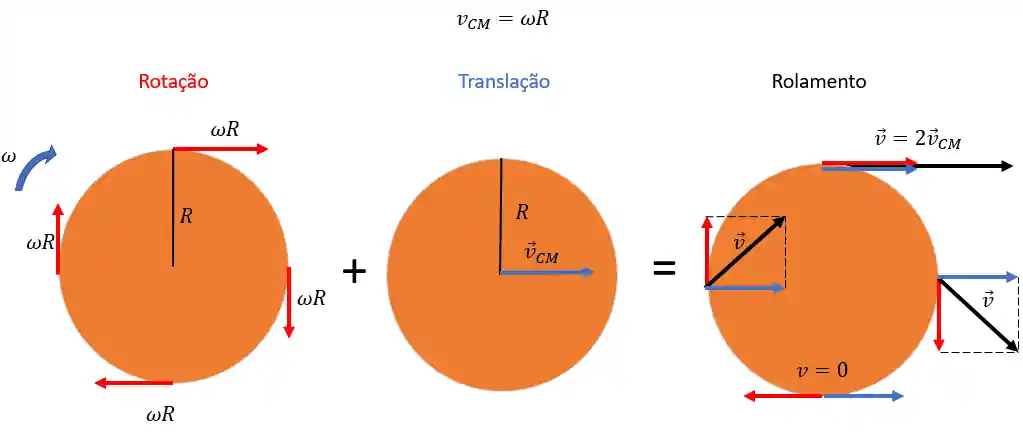
E aqui temos um rolamento acontecendo, mas e aí tem deslizamento ou não?
O que é Rolamento sem deslizamento?
Respondendo a pergunta acima, na figura que foi mostrada, o rolamento é sem deslizamento, mas o que isso significa?!
O rolamento sem deslizamento é caracterizado pela velocidade no ponto de contato com o solo ser igual a
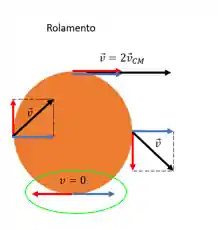
Ou seja, o ponto onde a velocidade toca o solo está em repouso!
E por isso a gente pode usar a seguinte relação pra velocidade do centro de massa:
E se derivarmos essa equação em relação ao tempo temos também que:
Essas equações só serão válidas para rolamento sem deslizamento!
Força e Torque no Deslizamento
Imagina que a roda abaixo desce rolando uma montanha, sem deslizar.
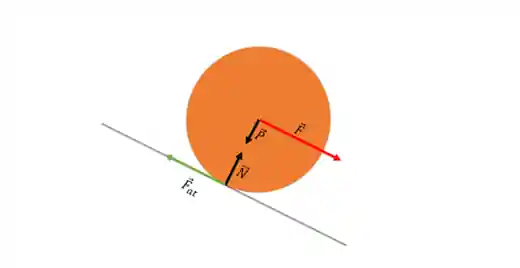
Se a massa da roda é
Na imagem acima, mostramos as forças que agem sobre a roda.
A força de atrito aponta para a esquerda. Quando você quiser descobrir o sentido da força de atrito, pense no ponto de contato. O ponto de contato
Para a direita, né? Por quê? Por que a velocidade do centro de massa aponta para a direita (e é ela que aumenta)! Então a
Outra coisa importante aqui é que estamos usando o atrito estático, viu? Isso por que esse ponto de contato está parado 😉
E agora? Como encontrar o valor da
Bem, estamos falando de rotação certo? Quais forças aqui exercem torque? Somente o atrito! Isso porque todas as outras forças apontam na direção do centro de massa da roda.
Se escrevermos a irmãzinha da segunda lei de Newton
O torque
Substituindo, temos:
Como estamos lidando com uma rotação sem deslizamento, podemos usar
Então:
E como a gente tá falando de um disco o momento de inércia é dado por:
Enfim a relação da
Agora podemos voltar para a nossa outra equação:
Isolando a aceleração:
Substituindo os valores então, temos:
Energia Mecânica no Rolamento sem Deslizamento
E se a nossa roda estivesse aqui? Qual vai ser a velocidade lá em baixo se a roda está em repouso, e a altura é
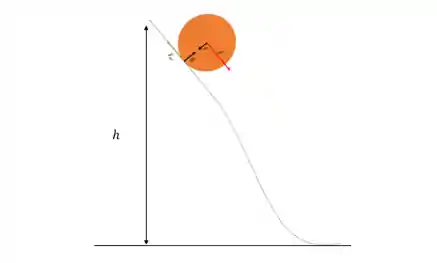
Se não há deslizamento podemos dizer que há conservação de energia mecânica que é composta de:
Onde:
Mas caramba, a gente não falou de força de atrito aqui? A energia se conserva nesse caso?
A resposta é SIM!
Mas como isso?
No caso de um rolamento sem deslizamento, o ponto de contato com o solo está parado certo? É nesse ponto que o atrito atua também.
A energia que o atrito tiraria do sistema teria que ser dada pelo seu trabalho
Só que o ponto de contato da roda com o solo está parado! Ou seja, o deslocamento é
Então reescrevendo a equação da energia mecânica com as equações de cada energia:
E se liga se a roda está em repouso tanto a energia de translação quanto a de rotação iniciais serão 0, e como a altura lá em baixo é zero a energia potencial também será
Substituindo o momento de inércia:
Substituindo o
Isolando a velocidade:
Substituindo os valores:
Aweee!
E repara, no final toda a energia potencial acabou se convertendo em cinética de translação e rotação, aumentando a velocidade do corpo.
Curtiu nosso conteúdo?!
Confere então esse resumo de Rolamento sem deslizamento em vídeo! 👇
Agora vamos praticar com exercícios?