Rolamento com Deslizamento
Produzido por Ludovic BeghinTeoria
Introdução
Se você já viu rolamento sem deslizamento, lembra como calculávamos a velocidade e aceleração angular do movimento certo? Mas lembra que a velocidade no ponto que o objeto tocava o chão era zero? E se a velocidade for diferente de zero nesse ponto o que vai acontecer?
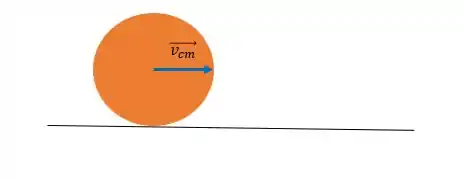
Se antes o objeto só girava, agora ele também desliza e faz os dois movimento juntos!
Se há deslizamento, aquele bizu da velocidade do ponto em contato com o chão ser zero não vale, assim o ponto não está em em repouso. Sem esse ponto em repouso, somos incapazes de usar aquelas relações diretas entre velocidade linear e velocidade angular.
Diferente do rolamento sem deslizamento, como o ponto de contato se move, o atrito que aparece é o cinético..
Temos dois casos possíveis:
-Anda mais rápido do que gira
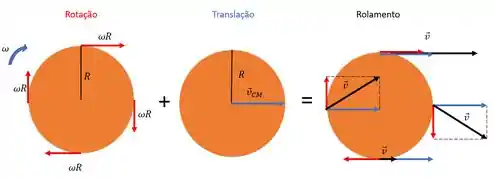
Mas e aí, esse tipo de rolamento vai sempre deslizar? A resposta é não!
O rolamento vai deslizar até que em um certo ponto, voltará a ser rolamento sem deslizamento e porquê? Por causa do atrito!
O atrito no caso de andar mais rápido que gira vai ser responsável por diminuir a velocidade do centro de massa e aumentar a velocidade angular até chegar no ponto em que:
Aqui o deslizamento para, e passamos a considerar o movimento sem deslizamento e toda aquela consideração vale.
Como o atrito é sempre contrário ao movimento podemos representa-lo dessa forma na figura abaixo.
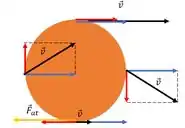
E repara na figura que é como a gente viu ali em cima, ele está no sentido oposto da velocidade do centro de massa e no mesmo sentido da velocidade angular.
O outro caso é quando o corpo:
Gira mais rápido do que anda
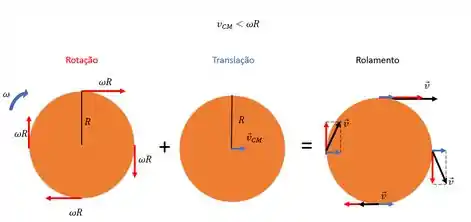
E o atrito? Moleza né? Tem que estar no sentido contrário da velocidade no ponto de contato.
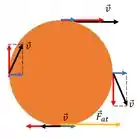
Nesse caso aqui, ele acelera a velocidade do centro de massa e diminui a velocidade angular mas de novo, tende ao ponto onde o deslizamento para pois chega na situação
Show! Mas como se trabalha com isso?
Rolamento com deslizamento
Se liga nesse exemplo:
Um disco de massa e raio é lançado, no instante com velocidade em um plano que possui coeficiente de atrito cinético com o disco. Depois de quanto tempo o disco pára de deslizar? A velocidade angular é nula no instante inicial.
As forças que agem no disco são:
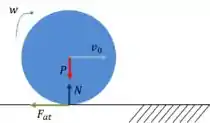
Se ligou que a aponta para a esquerda? É o caso em que ele gira menos do que anda e isso pois . O ponto de contato está se movendo para a direita e a força de atrito se opõe a esse movimento.
Se formos calcular o torque resultante no corpo escolhendo o centro do disco como referência, temos:
E como a força de atrito é cinética, temos que o módulo dessa força é constante.
Aqui no rolamento com deslizamento podemos usar essa fórmula? A resposta é SIM! Isso por que o atrito cinético só tem um valor possível (diferente do atrito estático).
Como o disco não executa movimento na vertical,
Substituindo:
Reunindo os resultados:
Com o valor do torque, conseguimos encontrar o valor da aceleração angular usando a segunda lei de Newton da rotação!
Como a gente tá falando de um disco o momento de inércia é:
E substituindo:
Assim a velocidade angular é dada por
Como , a equação da velocidade angular substituindo a aceleração é:
Agora vamos olhar o movimento de translação. A segunda lei de Newton fica
E a velocidade do disco é dada por
Repara que não usamos , já que estamos falando de um rolamento com deslizamento!!!
Beleza, mas e aí?
Vimos que a velocidade linear está diminuindo e que a velocidade angular está aumentando.
A pergunta que queremos responder é quando o corpo para de deslizar e começa a rolar sem deslizamento.
Isso vai acontecer quando em um dado intervalo de tempo obedecermos a condição de não deslizamento
Já temos e ! Assim
Isolando o tempo
Substituindo:
Agora rearrumando em função de t:
Ou seja, a partir desse tempo que acima que o corpo começa a rolar sem deslizar!
E se por acaso o nosso exemplo fosse do caso que gira mais do que anda? O jeito de calcular seria muito parecido, mas em primeiro ponto isso aqui mudaria.
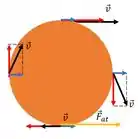
Nesse caso a se opõe ao giro, como mostrado e pra resumir o que vai mudar vai ser:
E aqui a aceleração vai ser positiva, diferente do ultimo caso e aí é só ir substituindo os valores no mesmo processo até encontrar que:
E dali em diante as contas seguem bem parecidas, a questão é só observar quem começa maior se é ou se é isso vai definir se o maior movimento é de translação ou rotação.
Partiu exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
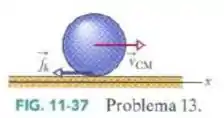
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 319-13.
Um jogador de boliche arremessa uma bola de raio ao longo de uma pista. A bola (Fig. 11-37) desliza sobre a pista com velocidade inicial e a velocidade angular inicial . O coeficiente de atrito cinético entre a bola e a pista é . A força de atrito cinético , que age sobre a bola produz uma aceleração linear e uma aceleração angular. Quando a velocidade diminui o suficiente e a velocidade angular aumenta o suficiente, a bola pára de deslizar e passa a rolar suavemente. (a) Qual é o valor de em termos de nesse instante? Durante o deslizamento, quais são (b) a aceleração linear e (c) a aceleração angular da bola? (d) Por quanto tempo a bola desliza? (e) Que distância a bola desliza? (f) Qual é a velocidade linear da bola quando começa a rolar suavemente?
Passo 1
Como dito no enunciado, o movimento da bola é dividido em duas partes:
- Deslizamento: A força de atrito age diminuindo a velocidade linear e aumentando a velocidade angular, até esta última chegar no valor certo para a bola começar a rolar;
- Rolamento: A força de atrito cinético deixa de agir e a bola entra em um movimento regular de translação e rotação.
Se a velocidade linear e a velocidade angular estão mudando, temos aceleração linear e aceleração angular agindo! Vamos fazer o diagrama de corpo livre da bola pra tentar entender:
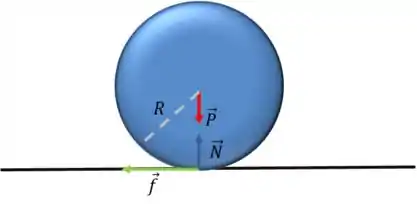
Agora vamos analisar como essas forças agem em cada movimento: rotação e translação.
Passo 2
Na translação, temos que a bola não se move na vertical, portanto, pela primeira lei de Newton:
Vamos arbitrar que o eixo cresce para a direita, no mesmo sentido da velocidade inicial da bola. Portanto, usando a segunda lei de Newton no eixo horizontal:
é a força de atrito cinético, portanto, tem valor constante:
E então:
Substituindo os valores:
Isso responde a letra (b), mas vamos guardar o nosso resultado!
Passo 3
Já para a rotação, temos que, em relação ao centro de massa da esfera, somente a força realiza torque, portanto:
Sabemos que tem valor constante:
Se usarmos a segunda lei de Newton da rotação:
O momento de inércia da esfera é tabelado:
Portanto:
E conseguimos o valor para a aceleração angular:
Substituindo os valores:
Isso responde a letra (c)!
Passo 4
Aprendemos que a característica principal do rolamento sem deslizamento é:
Substituindo os valores:
Isso nos responde a letra (a)!
Passo 5
Agora nós temos a relação entre e , bem como essas duas grandezas variam com o tempo, saca só:
Juntando tudo, temos:
Dessa equação, já temos os valores de:
- , dado no enunciado, é igual a
- , encontrado no Passo 2, é igual a
- , dado no enunciado, é igual a
- , encontrado no Passo 3, é igual a
Substituindo os valores:
Show! Estamos quase lá! Isso aí já responde a letra (d).
Passo 6
Com o tempo que a bola fica deslizando, é fácil encontrar as respostas das letras (e) e (f).
Pra descobrirmos a distância, vamos usar a equação clássica da cinemática:
Com:
- Queremos descobrir quanto ela andou, portanto,
- , dado no enunciado, é igual a
- , encontrado no Passo 2, é igual a
- , encontrado no Passo 5, é igual a
Substituindo tudo:
Respondendo, assim, a letra (e).
Passo 7
É agora hein! Pra terminar! Só usar mais uma equação clássica da cinemática:
Onde:
- , dado no enunciado, é igual a
- , encontrado no Passo 2, é igual a
- , encontrado no Passo 5, é igual a
Substituindo:
Fechou! Respondemos o que faltava.
Resposta
Exercício Resolvido #2
PUCRIO-P3-2009.2-3 - A
Uma aro de massa e raio é lançado horizontalmente com uma velocidade inicial sobre uma superfície horizontal cujos coeficientes de atrito cinético e estático são e .
Calcule qual é a distância desde o ponto em que o aro toca a superfície até quando ele passa a rolar sem deslizar.
Passo 1
Sabemos que quando o aro começar a deslizar, uma força de atrito cinético irá atuar, produzindo uma aceleração linear e uma aceleração angular, então vamos montar as equações que regem o movimento do aro:
Passo 2
O movimento rotacional, será:
Onde é o momento de inércia do aro:
Recorrendo à cinemática para modelar as velocidades, temos:
Passo 3
Para que o aro pare de deslizar, temos que ter: , substituindo, temos:
Isolando o , descobriremos em que momento isso ocorre:
Ah...=0!
Agora podemos achar a distância!
Para o sistema, temos:
Resposta