Momento Angular
Produzido por Ludovic BeghinTeoria
O momento angular é uma relação entre a inércia de um corpo e sua velocidade angular. Ele é uma grandeza física vetorial que mede a quantidade de movimento de um corpo em rotação.
O Responde Aí preparou um vídeo super completo com tudo o que você precisa saber sobre momento angular, para você arrasar na prova de Física! Dá uma conferida! 👇
📢 Clique para saber mais:
Fórmula do Momento Angular
Imagina uma partícula de massa
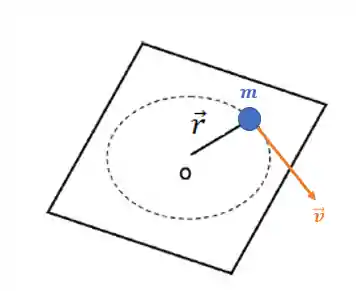
Para calcular o momento angular dessa partícula, usamos a seguinte fórmula:
Onde:
é o raio entre o objeto e o eixo de rotação; é a massa do objeto; é a velocidade linear do objeto.
-Beleza, mas da onde surgiu essa fórmula?! O momento angular tem alguma relação com o momento linear?!
Excelente pergunta, vamos entender isso agora!
Momento Angular x Momento Linear
O momento angular
Observando o exemplo acima, podemos ver que nossa partícula tem massa e uma certa velocidade tangencial
Mas não podemos esquecer que ela também está fazendo um movimento circular, então ela vai possuir uma certa quantidade de movimento angular, ou seja, momento angular!
Que podemos calcular com o seguinte produto vetorial:
Onde
Fazendo a substituição do momento linear na fórmula do momento angular de uma partícula:
Que é exatamente a fórmula que vimos ali em cima!
Sentido do momento angular
O momento angular é uma grandeza vetorial, isso significa que ela possui módulo, direção e sentido.
Para descobrirmos o sentido do momento angular, a gente vai usar a regra da mão direita! Ela é bem simples, se liga na imagem abaixo:

Na regra da mão direita, fazemos os quatro dedos girarem no mesmo sentido que a partícula, e dessa forma o dedão vai apontar para a direção do momento angular.
Uma outra forma de escrever a regra da mão direita é: o dedo médio aponta para a direção do vetor velocidade; o dedo indicador aponta a direção do vetor distância, consequentemente, o polegar vai apontar pra direção do momento angular. Vamos pensar nesse primeiro caso aqui:
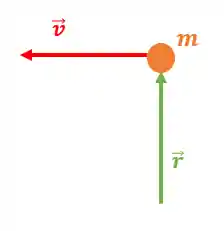
Pela regra da mão direita, teremos:
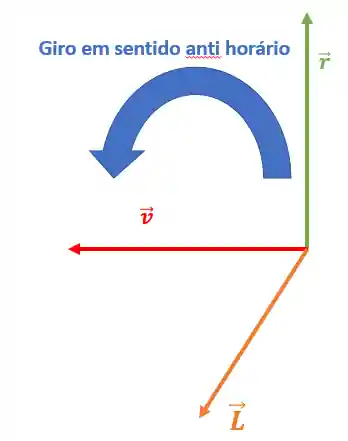
Maneiro, não é?!
Agora, vamos praticar com exercícios?
Fórmula do Momento Angular
Sentido do momento angular
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 325-84
Um avião de está voando em uma linha reta a , acima do solo. Qual é o módulo do momento angular do avião em relação a um ponto no solo verticalmente abaixo do local onde ele se encontra?
Passo 1
Essa aqui não é nada mais do que a aplicação da fórmula do momento angular:
Já que a velocidade e o vetor distância estão fazendo um ângulo de entre si. Se liga:
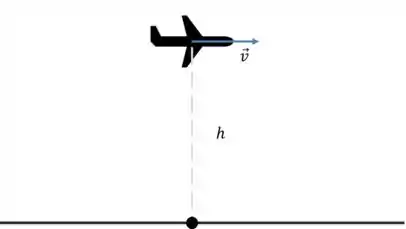
Então:
Resposta
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 320-27
No instante da Fig. 11-41, duas partículas se movem em um plano . A partícula possui uma massa de e uma velocidade e está a uma distância do ponto . A partícula possui uma massa de e uma velocidade e está a uma distância do ponto . Quais são (a) o módulo e (b) a orientação do momento angular resultante das duas partículas em relação ao ponto ?
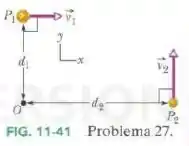
Passo 1
Essa é uma boa questão pra botar em prática o que você aprendeu sobre regra da mão direita!
Vamos usar o sistema de eixos dado na figura, onde o eixo aponta para fora da tela do seu computador.
Queremos o momento angular resultante, que é dado por:
Onde e são vetores que tem origem no ponto O e terminam nos pontos onde estão as partículas e , respectivamente.
Substituindo os valores das massas, bem como o módulo, direção e sentido das velocidades e das direções, temos:
Usando da regra da mão direita para calcular e :
Resposta
- Perpendicular ao plano , apontando para fora da tela.
Exercício Resolvido #3
UFRJ-P2-2012.1-ME7
Considere uma partícula de massa presa ao teto em um suporte fixo por meio de um fio ideal de comprimento , formando um pêndulo. A partícula é solta a partir do repouso, com o fio esticado, a uma distância do teto; é o módulo da aceleração local da gravidade. Qual é o módulo do momento angular da partícula com relação ao ponto de sustentação do fio quando ela passa pelo ponto mais baixo da trajetória?
Passo 1
O momento angular nesse caso pode ser calculado como
Isso porque o braço, nesse caso é o comprimento do fio, que é .
Passo 2
Vamos agora calcular a velocidade da partícula que é o que precisamos para achar o seu momento linear .
Como temos conservação de energia:
A energia inicial é:
Isso porque ele parte do repouso. Considerando o ponto mais baixo da trajetória com altura zero.
A energia final é:
Igualando:
Passo 3
O momento linear fica igual a:
E seu momento angular fica igual a:
Resposta
Letra B
Exercício Resolvido #4
UFRJ-PF-2014.1-ME2
Três partículas de massas iguais a movem-se na ausência de forças externas com velocidades e . Num dado instante elas ocupam as posições indicadas na figura abaixo. O vetor momento angular total deste sistema de partículas em relação a origem do eixo de coordenadas da figura é
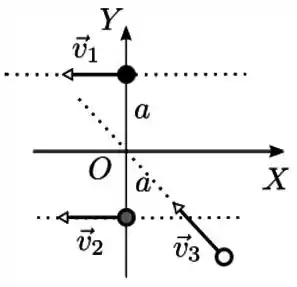
(a)
(b)
(c)
(d)
(e)
Passo 1
A gente calcula o momento angular de uma partícula em relação à origem com a fórmula:
seria como o braço da alavanca pro torque, a distância da direção da velocidade da partícula à origem, enquanto é seu momento linear.
O sinal é positivo quando o momento angular faz girar no sentido anti-horário e negativo se ele faz girar no sentido horário.
Passo 2
Vamos começar pela partícula de velocidade .
Ela está a uma distância da origem, e faz girar no sentido anti-horário, então o seu momento angular em relação à origem é:
Passo 3
A partícula de velocidade também está a uma distância da origem, mas ela faz girar no sentido horário, então seu momento angular em relação à origem é:
Passo 4
Vamos finalizar com a partícula de velocidade . Repare que a direção dela aponta diretamente pra origem, então pra essa partícula temos . Logo,
Passo 5
Então o momento angular total desse sistema em relação à origem é dado por:
Resposta
Alternativa (a)
´
Exercício Resolvido #5
USP-P2-2015-3
A figura mostra a trajetória reta de uma partícula de massa no plano com velocidade constante . É INCORRETO afirmar sobre o movimento que:
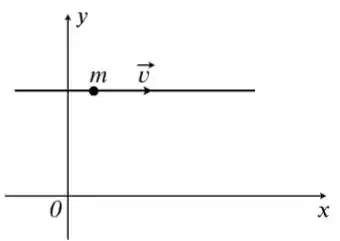
(a) o momento angular em relação a qualquer ponto do plano é constante.
(b) o momento angular em relação à origem é nulo.
(c) o momento angular em relação ao ponto de interseção da trajetória com o eixo é nulo.
(d) o torque total sobre a partícula é nulo.
(e) a força resultante sobre a partícula é nula.
Passo 1
Vamos analisar as alternativas uma a uma:
Alternativa (a): o momento angular em relação a qualquer ponto do plano é constante.
Pela fórmula:
Derivando dos dois lados:
Ou seja, o momento angular só varia na presença de um torque externo ao sistema. Como não tem nenhuma força externa atuando no sistema, também não tem torque externo. Logo o momento angular não varia.
Então a alternativa (a) é verdadeira.
Alternativa (b): o momento angular em relação à origem é nulo.
O momento angular pode ser calculado por:
Onde é o vetor posição em relação a algum ponto. Para que esse produto vetorial seja nulo, o vetor posição deve estar paralelo à velocidade.
O vetor posição da partícula em relação a origem não está paralelo a velocidade. Então a alternativa é a incorreta que estamos procurando!
Vamos olhar as outras só para ter certeza.
Alternativa (c): o momento angular em relação ao ponto de interseção da trajetória com o eixo é nulo.
Essa é a mesma coisa que a alternativa anterior, só que agora é em relação ao ponto de interseção com o eixo . E nesse caso, o vetor posição está em paralelo com a velocidade e o momento angular realmente será nulo.
Então a alternativa é verdadeira.
Alternativa (d): o torque total sobre a partícula é nulo.
Como já dissemos na alternativa (b), visto que não há força externa, também não haverá torque externo. Assim diz a fórmula:
Logo a alternativa é verdadeira.
Alternativa (e): a força resultante sobre a partícula é nula.
Também já dissemos que não possui força externa sobre a partícula. Isso pode ser provado pelo fato de a velocidade ser constante. Então pela fórmula:
Se não há aceleração, a força resultante é nula.
Resposta
Letra (b)
Exercício Resolvido #6
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 321-40
A Fig. 11-46 mostra o torque que age sobre um disco inicialmente estacionário que pode girar em torno do seu centro como um carrossel em função do tempo. Qual é o momento angular do disco em relação ao eixo de rotação nos intantes (a) e (b) ?
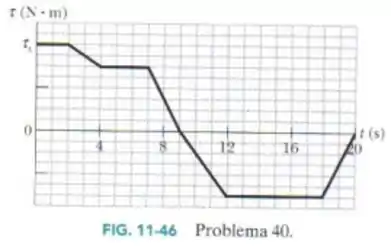
Passo 1
Aprendemos que, se temos um gráfico :
Então vamos lá:
Passo 2
- , retângulo de base e altura :
- , trapézio de base maior , base menor e altura 2:
- , retângulo de base e altura :
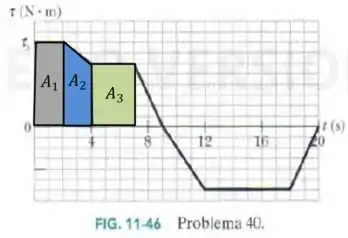
Calculando as áreas, tendo como base que cada quadradinho tem tamanho 1:
Portanto, como o disco está em estado estacionário(), temos:
Passo 3
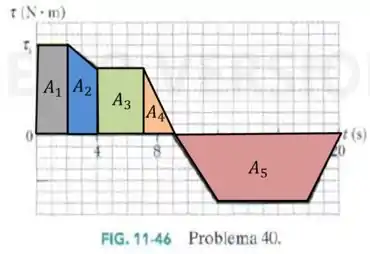
Já calculamos a soma de e , nos resta então calcular as outras duas áreas:
- , área de um triângulo de base e altura .
- , área de um trapézio de base maior , base menor e altura .
E então, lembrando que devemos diminuir a última área, já que está abaixo do eixo, temos:
Resposta
Exercício Resolvido #7
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 320-37
O momento angular de um volante com um momento de inércia de em relação ao eixo central diminui de para em . (a) Qual é o módulo do torque médio em relação ao eixo central que age sobre o volante durante esse período? (b) Supondo que uma aceleração angular constante, de que ângulo o volante gira? (c) Qual é o trabalho realizado sobre o volante? (d) Qual é a potência média do volante?
Passo 1
Aprendemos que:
Mas, como nesse item ele pede o torque médio:
Como foi pedido o módulo, a resposta da letra (a) é apenas o valor absoluto do torque médio.
Passo 2
Conhecemos a relação:
E, temos também a equação de torricelli da rotação, se liga:
Como o momento de inércia é uma constante:
Para encontrar o valor de , vamos usar a segunda lei de Newton da rotação:
Agora sabemos todos os valores, exceto :
Passo 3
Assim como o trabalho de uma força lá na translação era dado por:
Aqui é só mudar as letrinhas:
- A força vira o torque
- A distância vira o ângulo percorrido
Passo 4
A potência mantém a sua definição: trabalho realizado por tempo.
Resposta
(a)
(b)
(c)
(d)