Campo Elétrico Gerado por um Disco
Produzido por Bruno SoaresTeoria
Fala pessoal!
Além do caso das linhas de cargas, também vamos precisar aprender a calcular o campo elétrico gerado por discos, então vem comigo!
Campo Gerado por Disco de Cargas
Vamos pegar um disco de cargas, de raio , no plano , carregado uniformemente com uma carga positiva . E digamos que você precisa encontrar o campo elétrico em um ponto qualquer no eixo .
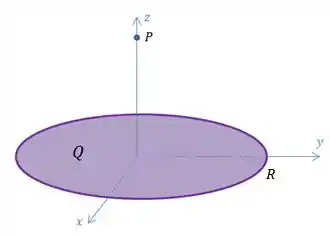
E para calcular o campo elétrico de um corpo extenso, o primeiro passo é dividi-lo em pedaços infinitesimais de carga , pois o campo elétrico gerado pelo corpo vai ser a soma do campo elétrico gerado por cada pedaço de carga.
Mas beleza, quem vai ser o nosso pedaço de carga nesse caso?
Quando tínhamos uma linha de carga, nós pegávamos um pedaço infinitesimal de carga que era um ponto da linha de carga.
Agora que temos um disco de carga, nós vamos pegar um pedaço infinitesimal de carga que será uma linha de carga, nesse caso, uma circunferência de raio .
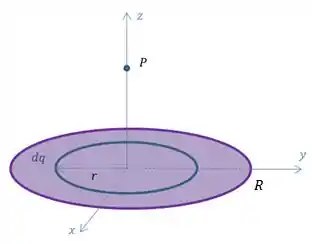
Agora temos que olhar para o campo elétrico gerado por esse anel de carga, e o lance aqui é encontrar a simetria do problema.
Se olharmos para o campo elétrico de dois pedaços de carga diametralmente opostos desse anel de cargas, nós vamos ter algo assim:
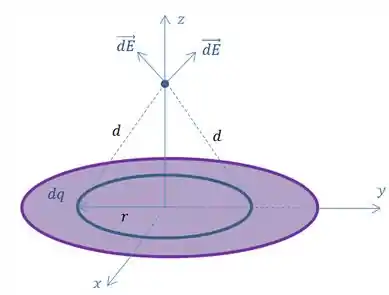
Repara só que a componente em desses campos elétricos vão se anular e vai sobrar apenas a componente em :
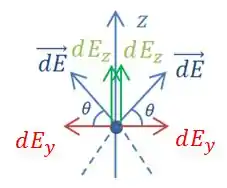
E isso é válido para todos os pontos do anel de cargas, pois todos eles terão um outro ponto diametralmente oposto que irá anular a componente do campo, ficando apenas com a componente que aponta na direção do eixo .
Como o anel de cargas gera um campo na direção do eixo , o disco de cargas (que é a soma de vários anéis de carga), também vai ter um campo na direção do eixo :
E para encontrar essa componente do campo no eixo , faremos:
Mas quem é esse ? Se olharmos na figura em que o está decomposto, vemos que ele vai ser:
Por fim, podemos escrever então que:
Simetria feita, agora está na hora de substituir esses valores aí, e agora vai entrar a trigonometria :)
A distância do pedaço infinitesimal de carga até o ponto e o são valores que iremos encontrar a partir do seguinte triângulo:
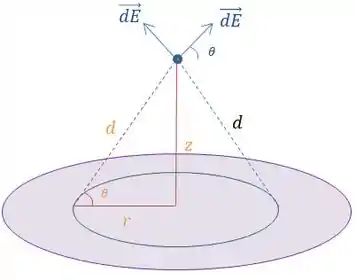
A distância é a hipotenusa do triângulo retângulo, portanto:
E o ângulo do triângulo é o mesmo ângulo lá do vetor , e achamos o seu seno assim:
E substituindo o , que acabamos de encontrar:
Agora é só substituir geral na fórmula lá!
Agora, você deve estar se perguntando, como eu integro esse negócio aí?

O que a gente precisa é trocar esse por um integrador que a gente consiga integrar.
Lá no início, eu disse que esse disco está uniformemente carregado. Como ele é um objeto em , ele possui uma densidade superficial de carga , que me dá a relação entre um pedaço de carga e um pedaço de área do disco.
Como esse valor é constante, pois o disco está uniformemente carregado, nós podemos escrever ainda que:
Mas esse aí, ainda não tá bom, mas se liga, a área de um círculo é o quê:
Deriva em função de ...
E substitui de volta, vamos ter o nosso em função de .
Se liga numa coisa, o do numerador é o raio dos anéis que são nossos pedaços infinitesimais de carga e o do denominador é o raio do disco.
(Pode ser que você encontre uma questão que te dê a densidade superficial, ao invés da carga e do raio do disco, aí o processo é o mesmo, só que ao invés de escrever em função da carga e do raio, você vai deixa-lo em função da densidade superficial ).
Agora substitui isso lá na fórmula de volta!
E tudo que é constante e não varia com o raio dos anéis de carga, vai sair da integral.
Antes de resolver, vamos colocar os limites de integração. Aqui queremos integrar todos os anéis de carga que compõe o disco de carga. Para isso, vamos variar o nosso integrador que é o raio do anel de carga , indo de até que é o raio do disco.
E essa integral aí, assusta né!

Mas relaxaaaaa, por que ela é resolvida por substituição, olha só:
E derivando...
Aplicando no nosso caso:
Ajustando tudo para integrar,
E por fim, voltamos com a variável e os limites de integração
E substituindo nossos limites:
Organizando um pouco mais, vou jogar o para dentro para poder cortar com o denominador da segunda fração...
E pronto, encontramos o campo elétrico gerado pelo disco de cargas, aí tendo o valor da carga, do raio do disco e da altura do ponto em relação ao disco, podemos encontrar o campo gerado!
E se o disco tiver carga negativa?

Nesse caso, a resposta é a mesma, só que ao invés do campo apontar para cima, ele apontaria para baixo!
É isso aí, partiu praticar?
Exercícios Resolvidos
Exercício Resolvido #1
PUCRIO-P1-2013.1-1- c
Uma barra delgada de comprimento é envergada até formar um semi-círculo, conforme mostra a Figura 1.
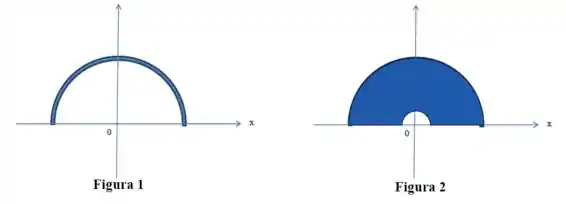
Se a barra tem uma densidade de carga uniforme , calcule o campo elétrico na origem.
Onde deveria ser colocada uma carga pontual de valor igual ao da carga total da barra para que o campo na origem fosse nulo?
Considere agora que esse semicírculo se torne um semi-disco de mesmo raio com um orifício concêntrico semicircular de raio e com uma densidade superficial uniforme , como mostrado na Figura 2. Calcule o campo elétrico na origem devido a esta nova configuração.
Passo 1
Para calcular o campo elétrico na origem, devido a barra carregada, podemos usar a equação do campo gerado por uma carga infinitesimal:
Pela simetria, vemos que dois pontos simétricos em relação ao eixo , produzem campos infinitesimais cujas componentes irão cancelar, sobrando apenas as componentes que estão se somando!
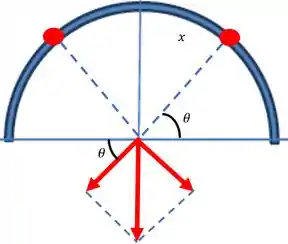
Então, queremos:
No nosso caso, temos , substituindo:
Integrando:
Onde , logo:
Passo 2
Para que o campo em seja nulo, o campo gerado pela carga deve ser igual em módulo ao campo gerado pelo fio, e de sinal oposto para poder cancelá-lo. O campo gerado pela carga é dado por:
Como a carga possui a mesma carga total da barra:
Substituindo e igualando ao valor do campo:
A carga , por ter mesmo sinal que a barra, deve ser colocada no lado oposto, ou seja:
Passo 3
Para determinar o campo na origem, devido o disco carregado, podemos partir do que já calculamos no item , para um semicírculo à uma distancia da origem, temos que o campo gerado é:
Integrando de até , temos:
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 47-35.
A que distância do eixo de um disco de plástico uniformemente carregado de de raio o módulo do campo elétrico é igual à metade do módulo do campo no centro do disco?
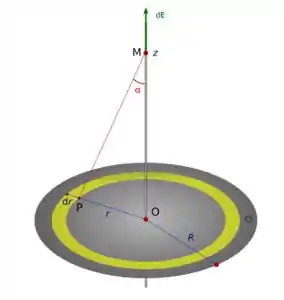
Passo 1
Observar que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenas rosquinhas de largura e raio como a indicada em verde na figura acima.
A área infinitesimal dessas rosquinhas vale a derivada da área do círculo de raio em relação a :
Passo 2
Calcular a carga infinitesimal da região verde, multiplicando a pequena área pela densidade superficial de campo, que é constante pois o disco está uniformemente carregado.
Passo 3
Note que a resultante do campo elétrico se encontra no eixo , devido à simetria do problema. Isso por que dois pontos do anel radialmente opostos dão campos de mesma intensidades e que somados dão um campo na direção como na figura abaixo
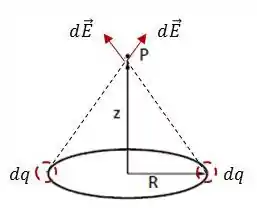
Então:
Passo 4
Determinar quem é o campo infinitesimal gerado por cada pedacinho verde da figura e substituir na equação encontrada.
Passo 5
Precisamos descobrir , para isso devemos projetar o campo infinitesimal do passo anterior no eixo .
Passo 6
Resolvendo a integral:
Agora o lance é resolver essa integral. GERALMENTE essa integral vem num formulário da sua prova, mas se não vier vamos ensinar aqui você a fazer! Pra isso pega aí aquela sua caneta/lapiseira/lápis especial e me acompanha, belê?
Passo 7
Primeiro de tudo, essa integral não sai direto! Pra isso temos que fazer uma substituição.
Olhando pra ela
Vamos ter que simplificar esse denominador. Como em cima tem um , a integral tá pedindo pra gente fazer a seguinte substituição
De forma que
E os limites de integração ficam
Então a nossa integral vai ficar
Essa integral vai ser
Assim a nossa integral fica
Finalmente
Voltando para o nosso campo
Supondo , vamos ter
Passo 8
Determinar o campo elétrico no centro do disco, que ocorre quando :
Queremos saber em que posição o campo vale a metade disso.
Passo 9
Logo:
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 47-37.
Um engenheiro foi encarregado de projetar um dispositivo no qual um disco uniformemente carregado de raio produz em um ponto sobre o eixo do disco a uma distância do plano do disco. Para economizar material decidiu-se substituir o disco por um anel com o mesmo raio externo e um raio interno . O anel tem a mesma densidade superficial de cargas que o disco original. Qual é a razão entre o novo campo no ponto e o campo antigo?
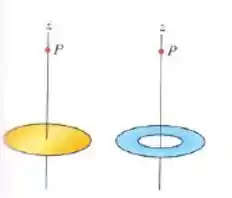
Passo 1
Observe que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenos anéizinhos de largura e raio como a indicada em verde na figura abaixo.
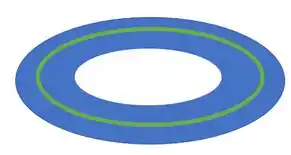
A área desse anelzinho vai ser o seu comprimento vezes a sua espessura
Passo 2
A carga infinitesimal da região verde, é dada pelo produto da pequena área pela densidade superficial de carga, que é constante pois o disco está uniformemente carregado.
Passo 3
Essa distribuição de carga tem uma simetria cilindrica. Isso significa se pegarmos dois pedaços do anel diametralmente opostos (como na figura) e somarmos o campo produzido por cada um deles, o campo resultante vai estar na direção
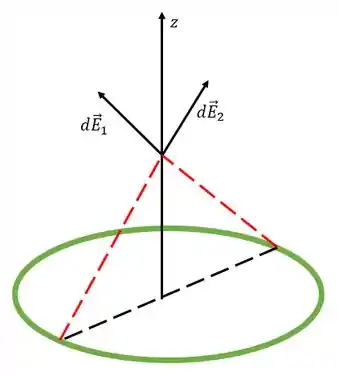
Então o nosso campo é da forma
Lembrando que isso tem que tá bem justificadinho na sua prova hein! Se falar que é assim só por causa da simetria dá ruim :/
Passo 4
Agora temos que montar a expressão pro campo infinitesimal do anel. Como todos os pontos do anel estão a mesma distância do ponto que queremos calcular o campo, vamos ter então
Onde .
Mas ainda falta uma coisa! Cada infinitésimo produz um campo inclinado em relação ao eixo e quando somamos todos os pedaços do anel, ficamos só com a componente na direção . Pela figura abaixo a componenente é dada por
E então
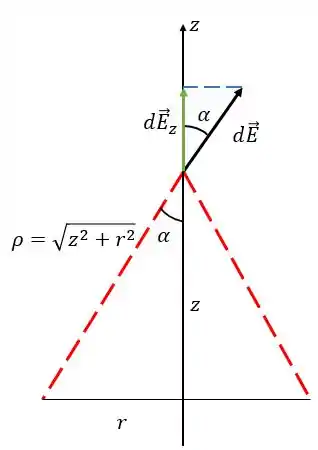
Pela figura temos que
Assim
Subsitituindo e
Passo 5
Resolvendo a integral no caso (A):
Os detalhes de como calcular esta integral estão demonstrados na teoria.
Passo 6
Resolver a integral no segundo caso (B), que é completamente parecido. Nessa situação, vamos apenas alterar os limites de integração.
O limite inferior se altera, quando devemos calcular o novo cosseno do ângulo :
Assim, o valor que encontramos é:
Passo 7
Queremos a razão:
Substituindo :
Logo:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 48-52.
Um elétron é liberado a partir do repouso no eixo central de um disco uniformemente carregado de raio . A densidade superficial de cargas do disco é . Determine o módulo da aceleração inicial do elétron se ele for liberado a uma distância do centro do disco de:
(a)
(b)
(c)
(d) Por que o módulo da aceleração quase não varia com a distância entre a carga e o disco?
Dado: Razão carga massa do elétron:
Passo 1
Temos a seguinte situação
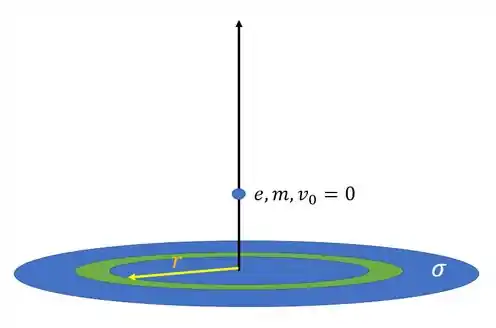
Observe que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenas rosquinhas de largura e raio como a indicada em verde na figura acima.
A área infinitesimal dessas rosquinhas vale a derivada da área do círculo de raio em relação a :
Passo 2
Vamos calcular a carga infinitesimal da região verde, multiplicando a pequena área pela densidade superficial de campo, que é constante pois o disco está uniformemente carregado.
Passo 3
Notar que o campo elétrico resultante se encontra no eixo , devido à simetria do problema. Então:
Passo 4
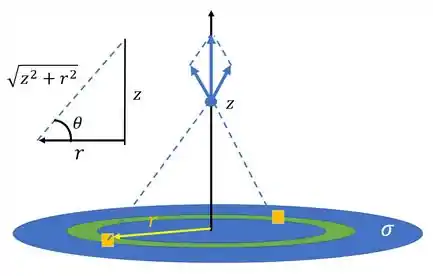
Temos que determinar quem é o campo infinitesimal gerado por cada pedacinho do disco carregado e substituir na equação encontrada.
Todos os pedacinhos do disco estão a uma distância do nosso ponto! Outro ponto importante é que devido a simetria o campo tem que apontar na direção . Para pegarmos essa componente basta multiplicar por que tá mostrado na figura acima, beleza?
Então temos
Pela figura
E já vimos que
Assim
Passo 5
Agora basta integrar!
Pra fazer essa integral é só fazer a substituição !
O resultado vai ser:
Passo 6
Podemos a partir do campo determinar a força, que é igual ao produto da massa do elétron pela aceleração que queremos determinar:
Logo:
Passo 7
Substituir os valores sugeridos no problema:
(a) Se
(b) Se
(c) Se
Passo 8
O módulo da aceleração quase não varia para menores distâncias entre a carga e o disco porque a resultante da força produzida pelas cargas próximas da borda do disco diminuir com a redução da distância entre o elétron e o centro do disco.
Quando a distância do elétron é muito menor que o raio do disco, o elétron “vê” esse disco como um plano infinito! Lembra como era o campo de um plano infinito? Ele não depende da distância da carga até o plano! A mesma coisa acontece aqui desde que a distância seja muito menor do que o raio do disco!
Outra forma mais matemática de ver isso é:
No limite , a gente pode fazer a razão tender a zero já que essa razão é um número muito pequeninho! Então nesse limite
Resposta
(a) Se
(b) Se
(c) Se
(d) O módulo da aceleração quase não varia para menores distâncias entre a carga e o disco porque a resultante da força produzida pelas cargas próximas da borda do disco diminuir com a redução da distância entre o elétron e o centro do disco.
Isso ocorre porque nessas posições essas forças quase se cancelam e apenas as cargas próximas ao centro do disco exercem influência no elétron.