Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Fluxo Elétrico

Ver Todos os Exercícios

Teoria

A lei de Gauss diz que “O fluxo elétrico através de uma superfície fechada é proporcional à carga líquida dentro dela”. Matematicamente, temos:

Onde:

  • é o fluxo de campo elétrico sobre uma superfície fechada, expresso em ;
  • é a carga que está envolvida pela gaussiana, a carga que está interna a essa superfície, expressa em ;
  • é a constante de permissividade do vácuo, que vale:

-Mas peraí, o que é fluxo elétrico? Aliais…o que é fluxo? 😖

Calma que a gente vai ver tudinho, passo a passo hoje e eu te garanto que não vai ficar nenhuma dúvida! Vamos começar entendendo o que é fluxo!

O que é Fluxo?

Imagine uma região, na qual temos um vetor


, e colocamos nessa região uma superfície plana de área AA. O que vai acontecer é que o vetor \vec{V}
V
 irá atravessar essa superfície, como nessa imagem:

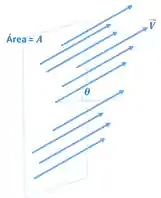
Fluxo sobre uma superfície
Fluxo sobre uma superfície

O vetor atravessando a superfície gera um fluxo desse vetor sobre essa superfície. Mas como calculamos esse fluxo?

Para isso vamos decompor esse vetor em duas componentes, uma perpendicular à área e outra paralela ao plano .

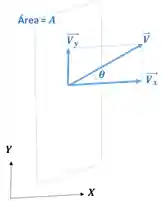
Decomposição do Vetor
Decomposição do Vetor

Note que a componente não atravessa a superfície plana, pois ela é paralela a essa superfície, então, ela não contribui para o fluxo do vetor nessa superfície. Então, apenas a componente será levada em consideração para calcular a área.

Além disso quanto maior for a área, , maior será a quantidade da componente do vetor irá atravessar a superfície. Então, podemos dizer que o fluxo é proporcional à área e à componente. Podemos escrever isso como:

Onde é o fluxo. Podemos escrever também a componente em função do módulo do vetor , como:

Então, o fluxo pode ser escrito como:

Se nós definirmos um vetor área perpendicular à superfície e com módulo igual à área dessa superfície, a gente também pode calcular o fluxo usando um produto escalar entre o vetor área e o vetor . Ou seja:

Obtemos o mesmo resultado!

📢 Clique para saber mais:

Como calcular o Fluxo do Campo Elétrico

Agora que sabemos o que é o fluxo e como calculá-lo podemos falar sobre o fluxo elétrico!

Quando falamos de fluxo elétrico, estamos falando do vetor campo elétrico atravessando uma superfície, então, temos que no fluxo elétrico o vetor genérico , que falamos lá no início, será o nosso vetor campo elétrico . Nós iremos representar o fluxo elétrico como:

Mas no fluxo elétrico temos uma pequena complicação. A superfície que vamos considerar nem sempre é uma superfície plana, podemos ter superfícies de vários formatos. Então, para calcularmos o fluxo elétrico precisaremos calcular uma integral:

Agora vamos a algumas informações importantes:

Um campo elétrico paralelo à superfície não gera fluxo

Isso acontece pois o ângulo entre o vetor normal e o vetor campo elétrico é e como cosseno de é zero o produto escalar entre o vetor área e o vator campo será zero.

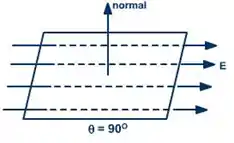
campo elétrico paralelo à superfície
campo elétrico paralelo à superfície

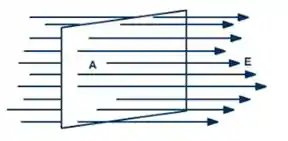
O fluxo elétrico gerado pelo campo é maior quanto mais próximo de 0° for o ângulo entre o vetor normal e o campo.

Como podemos observar na figura abaixo:

fluxo elétrico gerado pelo campo
fluxo elétrico gerado pelo campo

Agora vamos praticar com exercícios?

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 68-1.

A superfície quadrada da figura tem 3,2 m m de lado e está imersa em um campo elétrico uniforme de módulo E = 1800 N C e com linhas de campo fazendo um ângulo de 35 º com a normal como mostra a figura.

Tome essa normal como “apontando para fora”, como se a superfície fosse a tampa de uma caixa. Calcule o fluxo elétrico através da superfície.

Passo 1

O fluxo elétrico pode ser calculado como o produto escalar entre o vetor campo elétrico e o vetor área:

Φ e = E → . A → = E . A . c o s ⁡ ( 180 - θ )

Fica muito atento com a questão do ângulo! Olha essa figura aqui

θ é o ângulo que a direção do campo forma com a normal. Mas a gente precisa do ângulo entre os vetores! Ou seja, temos que colocar a nossa palma da mão em um deles e ir em busca do outro! Por isso o ângulo é 180 - θ .

Substituindo os valores fornecidos no enunciado:

E . A . cos ⁡ θ = 1800 N C . 3,2.10 - 3 m 2 . cos ⁡ 145 º = 1800 N C . 3,2.10 - 3 m 2 . - 0,82 = - 0,015 N . m 2 C

Resposta

Φ e = - 0,015 N . m 2 C

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 69-2.

Um campo elétrico dado por:

E → = 4 . i ^ - 3 . y 2 + 2 j ^

Atravessa um cubo com 2 m de aresta posicionado na forma demonstrada na figura. ( E é dado em newtons por Coulomb e x em metros). Determine o fluxo elétrico:

(a) através da face superior,

(b) através da face inferior,

(c) através da face da esquerda,

(d) através da face da traseira.

(e) Qual é o fluxo elétrico total através do cubo?

Passo 1

O fluxo do campo elétrico em uma superfície é dado por

Φ = ∫ E → ⋅ d A →

Quando o campo é constante ao longo da superfície

Φ = E → ⋅ A →

Onde A → é o vetor normal à superfície e que tem módulo igual a área da superfície. Como é um cubo de lado 2 m , a área de cada face é 4 m 2 . Assim, o módulo do vetor área vale 4. A direção e o sentido dele vão ser dadas de acordo com cada face. Acompanha aqui comigo.

Passo 2

Começando pela parte mais fácil, as faces de frente e de trás:

A normal dessas faces estão na direção ± k ^ . Assim o nosso fluxo pra esses dois caso vai ser\

Φ = E → ⋅ A →

Φ = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ ± 4 k ^

Como o produto interno entre o campo e o vetor normal de ambas as faces vão ser zero, temos:

Φ F R E N T E = Φ A T R A S = 0

Passo 3

Agora vamos olhar pras faces da esquerda e da direita:

Pra face da esquerda a normal tá na direção - i ^ , enquanto que pra face da direita a normal tá na direção i ^ . Assim

Φ E S Q U E R D A = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ - 4 i ^ = - 16   m 2 N / C

E

Φ D I R E I T A = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ 4 i ^ = 16   m 2 N / C

Passo 4

Agora na face de cima e na de baixo os vetores normais estarão nas direções ± j ^

Na superfície de cima

Φ C I M A = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ 4 j ^ = - 12 ( y 2 + 2 )

E caraca.... sobrou um y no final da conta! Pra sumir com ele basta substituir o seu valor! Na superfície de cima y tem um valor constante que é 2 . Assim

Φ C I M A = - 12 y 2 + 2 = - 12 2 2 + 2

Φ C I M A = - 72   m 2 N / C

Já na superfície de baixo

Φ B A I X O = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ - 4 j ^ = 12 ( y 2 + 2 )

O valor de y nessa superfície é 0

Φ B A I X O = 12 y 2 + 2 = 12 0 2 + 2

Φ B A I X O = 24   m 2 N / C

Passo 5

Vamos interpretar o resultado. É verdade que a questão não pediu todos os fluxos, mas o legal de fazer isso é que vamos poder interpretar o problema. Representando os fluxos em uma tabela:

Podemos ver que a soma não dá zero. Isso significa, fisicamente, que existe alguma carga dentro do cubo ;)

Resposta

(a) através da face superior, - 72 N . m 2 C

(b) através da face inferior, 24 N . m 2 C

(c) através da face da esquerda, - 16   N . m 2 C

(d) através da face da traseira, 0

(e) Fluxo elétrico total através do cubo:   - 48   N . m 2 C

Exercício Resolvido #3

UFF-LISTA2-3

Um retângulo de 2,0   c m   ×   3,0   c m situa-se no plano x z . Qual será o valor do fluxo elétrico através do retângulo se:

a )   E = 50 i + 100 k   N / C ?

b )   E = 50 i + 100 j   N / C ?

Passo 1

Para resolver essa questão, devemos lembrar da definição de fluxo elétrico, temos:

Φ = A ∙ E

Antes de analisar cada campo, vamos primeiro determinar o vetor área desse retângulo, lembrando que o vetor área aponta na direção normal à área, por se tratar de um retângulo no plano x z , o vetor área será:

A = 2,0 × 10 - 2 .   3,0 × 10 - 2   j

A = 6,0 × 10 - 4   m 2   j

Veja que temos que passar de centímetros para metros!

Pronto, agora é só efetuar o produto escalar com cada campo par achar o fluxo, se liga!

Passo 2

a )

Para   E = 50 i + 100 k , temos:

Φ a = A ∙ E

Φ a = 6,0 × 10 - 4   j ∙ 50 i + 100 k

Φ a = 0

Nesse caso, o fluxo elétrico será nulo!

Passo 3

b )

Para   E = 50 i + 100 j , temos:

Φ a = A ∙ E

Φ b = 6,0 × 10 - 4   j ∙ 50 i + 100 j

Φ b = 6,0 × 10 - 2   N . m 2 / C

Resposta

a ) Φ a = 0

b ) Φ b = 6,0 × 10 - 2   N . m 2 / C

Exercício Resolvido #4

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 69-4.

Em todos os pontos da superfície do cubo da figura, o campo elétrico é paralelo ao eixo z , O cubo tem 3 m de aresta. Na face superior do cubo, E → = - 34 k ^ N C , na face inferior, E → = 20 k ^ N C . Determine a carga existente no interior do cubo.

Passo 1

O campo elétrico possui a direção do eixo z . Então, o fluxo em todas as faces que não sejam nem a face de cima e nem a face inferior é nulo. Pois nas demais faces os campos elétricos são ortogonais aos vetores normais. Logo:

Φ E S Q U E R D A = Φ D I R E I T A = Φ F R E N T E = Φ T R A S = 0

Passo 2

Então o nosso problema se resume a calcular o fluxo na parte de cima e na parte de baixo. Na parte superior o campo vale:

E → = - 34 k ^ N C

O vetor normal nessa face possui sentido oposto:

n ^ S U P E R I O R = k ^

Então, o fluxo vale o produto entre a área e o campo com o sinal negativo:

Φ S U P E R I O R = - 34 k ^ . 3 2 k ^ = - 306   k ^ ⋅ k ^ = - 306 N . m 2 C

Passo 3

Fazemos a mesma coisa na face de baixo, mas aí o valor do campo muda:

E → = 20 k ^ N C

O vetor normal nessa face possui sentido oposto ao campo também:

n ^ I N F E R I O R = - k ^

Então, o fluxo vale o produto entre a área e o campo com o sinal negativo:

Φ I N F E R I O R = 20 k ^ . - 3 2 k ^ = - 180 k ^ ⋅ k ^ = - 180 N . m 2 C

Passo 4

Calcular o fluxo total:

Φ T O T A L = - 306 - 180 = - 486 N . m 2 C  

Passo 5

Aplicar a lei de Gauss:

Φ T O T A L = - 486 N . m 2 C = Q I N T ϵ 0 →

Q i n t = - 486.8,85.10 - 12 = - 4301.10 - 12 C = - 4,3   n C

Resposta

Q i n t = - 4,3   n C

Exercício Resolvido #5

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 69-5.

Uma carga pontual de 1,8   μ C está no centro de uma superfície gaussiana cúbica de 55   c m de aresta. Qual é o fluxo elétrico através da superfície?

Passo 1

É complicado calcular o fluxo elétrico em uma superfície cúbica.

Aqui a ideia é aplicar a lei de Gauss ao contrário: conhecendo a carga, podemos saber o fluxo e ele independe do formato da superfície gaussiana!

Então:

Φ = Q I N T ϵ 0 = 1,8.10 - 6 8,85.10 - 12 = 0,2.10 6 = 2.10 5 N . m 2 C  

Resposta

2.10 5 N . m 2 C  

Exercício Resolvido #6

UFRJ-P1-2011.1-ME01

Numa região do espaço de interesse, existe um campo elétrico constante (uniforme e estacionário), na direção e sentido de x ^ . Nessa mesma região, temos uma superfície cúbica abstrata, que encerra uma partícula (pontual) de carga Q > 0 localizada no seu centro. Três das faces do cubo estão assinaladas na figura: as faces 1 e 3 são paralelas ao plano Y Z , ao passo que a face 2 é paralela ao plano X Z . Em relação ao fluxo Φ i ( i = 1 , 2 , 3 ) do campo elétrico através de cada uma dessas faces (com orientação do vetor normal para fora, como usual), qual das alternativas abaixo é a correta?

  1. Φ 1 > Φ 2 > Φ 3
  2. Φ 1 > Φ 2 = Φ 3
  3. Φ 1 = Φ 2 > Φ 3
  4. Φ 1 = Φ 2 = Φ 3
  5. Φ 1 < Φ 2 < Φ 3

Passo 1

Como o fluxo de campo elétrico é dado pela seguinte fórmula:

ϕ = ∯ S   E → ∙ d A →

Podemos ver que, quando o vetor d A → aponta no mesmo sentido do campo temos fluxo positivo, ao passo que temos fluxo negativo quando eles apontam em sentidos opostos.

Passo 2

Portanto em função disto temos que a carga Q faz fluxo positivo em todas as três superfícies e com a mesma intensidade, por conta da simetria.

Já o campo externo tem um fluxo que depende da superfície. O vetor área da superfície 2 é perpendicular à ele, portanto o fluxo é zero.

ϕ e x t e r n o 2 = 0

Passo 3

Na superfície 1 ele é negativo, pois tem sentidos opostos:

ϕ e x t e r n o 1 < 0

Passo 4

E na superfície 3 ele é positivo, por terem mesmos sentidos:

ϕ e x t e r n o 3 > 0

Portanto, como os fluxos de Q são todos iguais e positivos, podemos afirmar seguramente que:

ϕ 3 > ϕ 2 > ϕ 1

Resposta

Letra e

Exercício Resolvido #7

Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 22.35, pp. 66.

O campo elétrico   E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uniforme em todos os pontos e aponta perpendicularmente para dentro da face, como mostra a Figura abaixo. As duas faces mencionadas possuem uma inclinação de 30 ˚ em relação à horizontal, enquanto  E → 1 e E → 2 são, ambos, horizontais; o módulo de E → 1 é igual a 2,50   ×   10 4   N / C e o módulo de E → 2 é igual a 7,0   ×   10 4   N / C .

  1. Supondo que nenhuma outra linha de campo atravesse as superfícies do paralelepípedo, determine a carga líquida contida em seu interior.

  2. O campo elétrico existente é produzido somente pelas cargas no interior do paralelepípedo ou pode ser produzido também por cargas existentes fora dele? Como se pode ter certeza disso?

Passo 1

a) Sabemos, pela lei de Gauss, que o fluxo total do campo elétrico no vácuo é dado por

Φ E T o t a l = ∮ S E → ⋅ d A → = Q l í q ε 0     ,

em que Q l í q é a carga líquida no interior da superfície fechada S .

Para gente matar essa questão, dá uma olhada na Figura acima, que representa a situação dada no exercício, mas desenhada de perfil. Blz? Assim facilita para a gente ver os ângulos entre os vetores   E → e   A → em cada face.

Seguindo de perto a Figura acima, repara que os vetores   A → 1 e   A → 2 têm o mesmo módulo, porque as duas faces têm mesma área, e ambos apontam perpendicularmente às respectivas faces, tranquilo??

Agora, como o campo elétrico em cada uma das faces é uniforme, ou seja, tem o mesmo valor em todos os pontos sobre a área de cada face, então, o fluxo para a face 1 pode ser escrito como

Φ E 1 = E → 1 A → 1 cos ⁡ ( 60 ˚ )   ,

e para a face 2

Φ E 2 = E → 2 A → 2 cos ⁡ 240 ˚ .

Lá da lei de Gauss, a gente pode escrever a carga líquida Q l í q dentro do paralelepípedo como

Q l í q = ε 0 Φ E T o t a l = ε 0 Φ E 1 + Φ E 2  

∴

Q l í q = ε 0 E → 1 A → 1 cos ⁡ 60 ˚ + E → 2 A → 2 cos ⁡ 240 ˚ .

Como A → 1 = A → 2 = A e cos ⁡ 240 ˚ = - cos ⁡ ( 60 ˚ ) , a gente pode simplificar a expressão acima para

Q l í q = ε 0 A E → 1 - E → 2 cos ⁡ 60 ˚   .

Jogando os valores dados no enunciado, chegamos a

Q l í q = ( 8,85 × 10 - 12 ) ( 0,05 × 0,06 ) 2,5 × 10 4 - 7 × 10 4 cos ⁡ 60 ˚

∴

Q l í q = - 5,98   ×   10 - 10   C   ,

o que mostra para a gente que a carga dentro do paralelepípedo é negativa. Por isso, parte das linhas de campo que vão para dentro dele terminam na carga Q l í q . O restante das linhas vai para fora dele.

Passo 2

b) Ainda que tenha carga dentro, existe um campo elétrico   E → 1 que sai do paralelepípedo, o que significa que este campo vai terminar em alguma carga fora do paralelepípedo. Além disso, o campo   E → 2 é produzido por cargas do lado de fora do paralelepípedo.

O importante aqui é o seguinte: embora apenas a Q l í q dentro da superfície fechada S contribua para o fluxo elétrico através da superfície fechada do paralelepípedo, as cargas que estão fora continuam contribuindo para o campo elétrico na superfície fechada S . Essa diferença é muito importante!!

Cargas elétricas fora da superfície fechada S produzem campo elétrico sobre essa superfície S, porém não contribuem para o fluxo elétrico total.

Resposta

  1. Q l í q = - 5,98   ×   10 - 10   C     ;

  2. Cargas fora do paralelepípedo (que é a superfície fechada S neste exercício!) contribuem para o campo sobre o paralelepípedo, mas não para o fluxo elétrico total Φ E T o t a l !!

Exercício Resolvido #8

Paul A. Tipler, Gene Mosca, Física para cientistas e engenheiros, Volume 2, 6˚ ed., Editora LTC, Problema 31, Capítulo 22, pp. 67.

Uma carga puntiforme ( q = + 2,00   μ C ) está no centro de uma esfera imaginária que tem raio igual a 0,5   m .

  1. Determine a área da superfície da esfera.

  2. Determine a magnitude do campo elétrico em todos os pontos na superfície da esfera.

  3. Qual é o fluxo do campo elétrico através da superfície da esfera?

  4. A sua resposta para o item c) mudaria se a carga puntiforme fosse deslocada de forma a permanecer dentro da esfera, mas não no centro dela?

  5. Qual é o fluxo do campo elétrico através da superfície de um cubo imaginário que tem aresta de 1,00   m de comprimento e que engloba a esfera?

Passo 1

a) A área da superfície de uma esfera é A = 4 π r 2 , em que r é o raio dessa esfera. Nesse caso, com os valores que são dados no exercício, a gente tem que

A = 4 π × 0,50 2 = 3,14   m 2 .

Passo 2

b) Como temos uma carga no interior da esfera, a lei de Coulomb mostra que o valor do campo que a carga q gera é

E = | E → | = 1 4 π ε 0 q r 2 = 7,19   ×   10 4   N C   .      

Passo 3

c) Como o vetor campo elétrico  E → tem o mesmo módulo em todos os pontos à distância r da carga pontual e E → é paralelo (para a carga positiva q ) ao vetor área   A → , então o fluxo do campo elétrico pode ser escrito como

Φ E = ∮ S E → ⋅ d A → = ∮ S E → d A → = E ∮ S d A = E A   ,

em que A = 4 π r 2 é a área da esfera gaussiana imaginária. Substituindo os valores que encontramos nos Passos 1 e 2, temos

Φ E = E A = 2,26   ×   10 5   N m 2 C   .

Passo 4

d) Nesse caso, ainda que a carga q estivesse em outra posição dentro da esfera imaginária, o fluxo elétrico seria exatamente o mesmo, pois, pela lei de Gauss, o fluxo do campo elétrico é diretamente proporcional à carga líquida que está dentro da superfície fechada.

Como nesse caso, a carga dentro da superfície fechada esférica é a mesma, o fluxo também o mesmo que no item c) anterior, portanto,

Φ E = 2,26   ×   10 5   N m 2 C     .

Passo 5

e) Agora, fica atento nisso aqui!! O cubo engloba a esfera que tem a carga q dentro dela. Blz?

Isso significa que as mesmas linhas de campo que passam pela área da esfera, passam também pela área do cubo. Apesar da geometria ser diferente entre essas duas superfícies imaginárias, o fluxo do campo elétrico é o mesmo, já que a carga no interior de ambas superfícies fechadas é a mesma. OK?

IMPOTANTÍSSIMO ISSO...GUARDA NO SEU CORAÇÃO, PORQUE ISSO NÃO CAI, DESPENCA NAS PROVAS!!

Resposta

  1. A = 4 π r 2 = 3,14   m 2   ;

  2. E → = E = 7,19   ×   10 4   N / C ;

  3. Φ E = E A = 2,26   ×   10 5   N m 2 C   ;

    4. .

  4. A resposta não mudaria, o fluxo continuaria sendo: Φ E = 2,26   ×   10 5   N m 2 C     ;

  5. Φ E = 2,26   ×   10 5   N m 2 C     .

Exercício Resolvido #9

Paul A. Tipler, Gene Mosca, Física para cientistas e engenheiros, Volume 2, 6˚ ed., Editora LTC, Problema 35, Capítulo 22, pp. 66.

Um cone circular reto imaginário, como mostrado na Figura abaixo, com ângulo de base θ e raio da base R está em uma região livre de cargas que tem um campo elétrico uniforme   E → = E 0 z ^ , cujas linhas de campo são verticais e paralelas ao eixo do cone, como na figura. Qual o fluxo do campo elétrico pela área lateral desse cone?

Passo 1

Bem, pra calcular o fluxo do campo elétrico temos que fazer a seguinte integral

Φ a r e a l a t e r a l = ∫ a r e a l a t e r a l E → ⋅ d A →

Só que calcular isso é osso, por que o campo elétrico faz um certo ângulo com essa superfície lateral o que é chatinho de fazer.... se fosse pra calcular pra base desse cone seria moleza xD

Passo 2

Mas existe um negócio que pode nos salvar! Esse negócio é a lei de Gauss!

O que a lei de Gauss diz? Como dentro desse cone não há carga, o fluxo no cone todo (que é uma superfície fechada) é nulo, ou seja

Φ c o n e = Q i n t ϵ 0 = 0

Só que o fluxo do campo elétrico dentro do cone pode ser dividido em duas partes

Φ c o n e = Φ b a s e + Φ a r e a l a t e r a l

Como Φ c o n e = 0

Φ a r e a l a t e r a l = - Φ b a s e

Aí sim!!! O fluxo do campo elétrico na base é bem mais tranquilo de calcular!

Passo 3

Agora vamos calcular Φ b a s e .

Como temos uma superfície fechada temos que orientar a normal da superfície apontando para fora do volume, assim, na base do cone a normal aponta para baixo, ou seja

d A → = d A - z ^

Assim

Φ b a s e = ∫ b a s e E → ⋅ d A → = ∫ b a s e E 0 z ^ ⋅ - d A z ^ = - E 0 ∫ b a s e d A

Φ b a s e = - E 0 A b a s e

Φ b a s e = - E 0 π R 2

Passo 4

Assim, finalmente temos que

Φ a r e a l a t e r a l = - Φ b a s e = - - E 0 π R 2

Φ a r e a l a t e r a l = E 0 π R 2

Resposta

Φ a r e a l a t e r a l = E 0 π R 2

Exercícios de Livros Relacionados

15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca