Exercícios de Fluxo de Campo Elétrico - Lista de Exercícios Resolvida
Questão 1
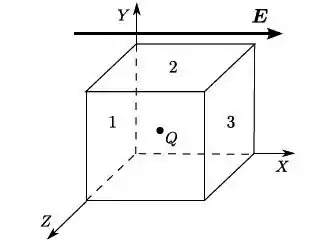
Um campo elétrico dado por:
Atravessa um cubo com de aresta posicionado na forma demonstrada na figura. ( é dado em newtons por Coulomb e em metros). Determine o fluxo elétrico:
(a) através da face superior,
(b) através da face inferior,
(c) através da face da esquerda,
(d) através da face da traseira.
(e) Qual é o fluxo elétrico total através do cubo?
Questão 2
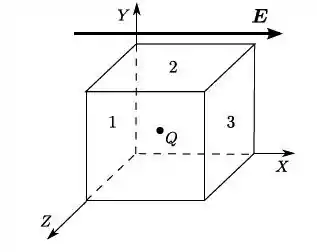
Numa região do espaço de interesse, existe um campo elétrico constante (uniforme e estacionário), na direção e sentido de . Nessa mesma região, temos uma superfície cúbica abstrata, que encerra uma partícula (pontual) de carga localizada no seu centro. Três das faces do cubo estão assinaladas na figura: as faces e são paralelas ao plano , ao passo que a face é paralela ao plano . Em relação ao fluxo (, , ) do campo elétrico através de cada uma dessas faces (com orientação do vetor normal para fora, como usual), qual das alternativas abaixo é a correta?
Questão 3
Em todos os pontos da superfície do cubo da figura, o campo elétrico é paralelo ao eixo , O cubo tem de aresta. Na face superior do cubo, , na face inferior, . Determine a carga existente no interior do cubo.
Questão 4
Uma carga puntiforme () está no centro de uma esfera imaginária que tem raio igual a .
- Determine a área da superfície da esfera.
- Determine a magnitude do campo elétrico em todos os pontos na superfície da esfera.
- Qual é o fluxo do campo elétrico através da superfície da esfera?
- A sua resposta para o item c) mudaria se a carga puntiforme fosse deslocada de forma a permanecer dentro da esfera, mas não no centro dela?
- Qual é o fluxo do campo elétrico através da superfície de um cubo imaginário que tem aresta de de comprimento e que engloba a esfera?
Questão 5
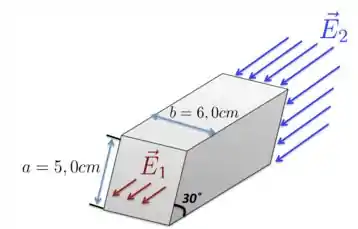
O campo elétrico em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico também é uniforme em todos os pontos e aponta perpendicularmente para dentro da face, como mostra a Figura abaixo. As duas faces mencionadas possuem uma inclinação de em relação à horizontal, enquanto e são, ambos, horizontais; o módulo de é igual a e o módulo de é igual a .
- Supondo que nenhuma outra linha de campo atravesse as superfícies do paralelepípedo, determine a carga líquida contida em seu interior.
- O campo elétrico existente é produzido somente pelas cargas no interior do paralelepípedo ou pode ser produzido também por cargas existentes fora dele? Como se pode ter certeza disso?
Questão 6
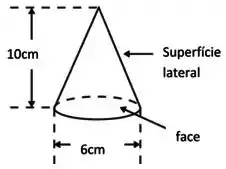
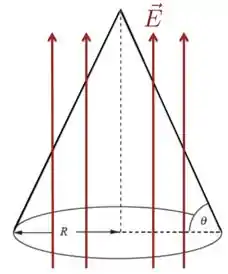
Um cone circular reto imaginário, como mostrado na Figura abaixo, com ângulo de base e raio da base está em uma região livre de cargas que tem um campo elétrico uniforme , cujas linhas de campo são verticais e paralelas ao eixo do cone, como na figura. Qual o fluxo do campo elétrico pela área lateral desse cone?
Questão 7
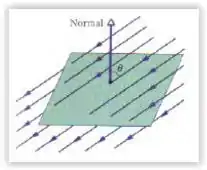
A superfície quadrada da figura tem de lado e está imersa em um campo elétrico uniforme de módulo e com linhas de campo fazendo um ângulo de com a normal como mostra a figura.
Tome essa normal como “apontando para fora”, como se a superfície fosse a tampa de uma caixa. Calcule o fluxo elétrico através da superfície.
Questão 8
Uma carga pontual de está no centro de uma superfície gaussiana cúbica de de aresta. Qual é o fluxo elétrico através da superfície?
Questão 9
Um retângulo de situa-se no plano . Qual será o valor do fluxo elétrico através do retângulo se:
?
?
Ver solução completaQuestão 10
Numa região do espaço de interesse, existe um campo elétrico constante (uniforme e estacionário), na direção e sentido de . Nessa mesma região, temos uma superfície cúbica abstrata, que encerra uma partícula (pontual) de carga localizada no seu centro. Três das faces do cubo estão assinaladas na figura: as faces e são paralelas ao plano , ao passo que a face é paralela ao plano . Em relação ao fluxo (, , ) do campo elétrico através de cada uma dessas faces (com orientação do vetor normal para fora, como usual), qual das alternativas abaixo é a correta?
Questão 11
Uma bola esférica de cobre tem raio e se encontra em posição concêntrica dentro de uma cavidade esférica de cobre de raio intermo . Na esfera interna existe uma elétrica .
(a) Use a lei de Gauss para calcular o campo elétrico na região .
Ver solução completaQuestão 12
12ª questão - O octaedro regular, representado na figura, é um poliedro com 8 faces iguais. Suponha que uma carga puntiforme seja colocada no centro geométrico do octaedro. O fluxo do campo elétrico através de cada face do octaedro vale:
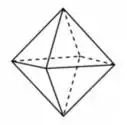
A)
B)
C)
D) zero
E) Não é possível calcular, pois o campo elétrico não é constante em cada face.
Ver solução completaQuestão 13
Uma partícula com carga encontra-se na origem do sistema de coordenadas mostrado na figura
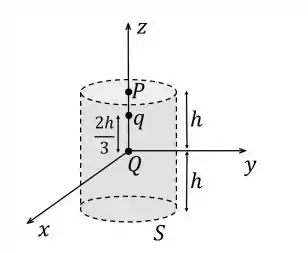
- Escreve a expressão do campo elétrico , devindo à carga , o ponto do eixo , localizado a uma altura do plano
- Qual carga , colcoada em anula o fluxo do campo elétrico através da superfície cilíndrica fechada que contém o ponto ?
- Qual carga , colocada em , anula o campo elétrico no ponto
Questão 14
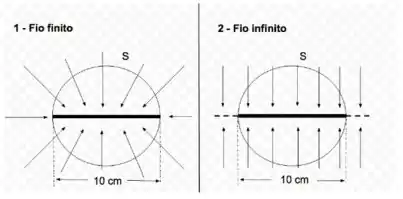
Considere os dois fios ilustrados na figura abaixo: um fio de comprimento e um fio infinito, ambos muito finos e carregados negativamente. A densidade de carga é a mesma para os dois fios. As setas representam as linhas de campo em cada caso. Para cada um dos fios, calculamos o fluxo elétrico através das superfícies (idênticas nos dois casos). Podemos afirmar que:
- Os fluxos são negativos nos dois casos, mas o fluxo no caso 1 é maior que o fluxo no caso 2.
- Os fluxos são negativos nos dois casos, mas o fluxo no caso 2 é maior que o fluxo no caso 1.
- Os fluxos são nulos nos dois casos.
- Os fluxos são positivos e iguais nos dois casos.
- Os fluxos são negativos e iguais nos dois casos.
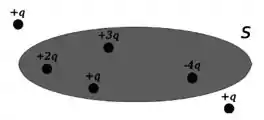
Questão 15
Considere o sistema de cargas na figura ao lado. O fluxo de campo elétrico total através da superfície é:
Questão 16
Em uma região do espaço existe um campo elétrico , se , e se , onde . Considere um cilindro imaginário de de comprimento e de raio da base, com centro na origem e eixo sobre o eixo . Qual é a carga total no interior do cilindro?
Questão 18
Q – Uma carga elétrica está localizada no centro de um cubo de lado . O fluxo do campo elétrico através de uma de suas laterais é:
Ver solução completaQuestão 19
A figura abaixo mostra algumas linhas de campo elétrico gerado por duas placas condutoras planas e paralelas com uma área muito maior que a separação entre elas, carregadas com densidade uniforme de cargas , e no seu interior uma esfera condutora neutra. e são duas superfícies fechadas que envolvem completamente uma das placas e a esfera respectivamente. O fluxo elétrico sobre as superfícies e são, respectivamente:
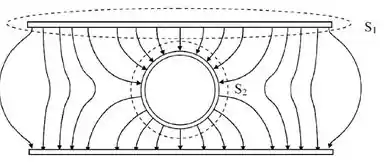
- e
- e
- e
- e
- e
Questão 20
Um sistema é formado por três partículas puntiformes de cargas , e . Considere este sistema em duas situações distintas, como mostram as figuras 1 e 2 abaixo. Em ambas, a superfície desenhada engloba apenas as cargas e .
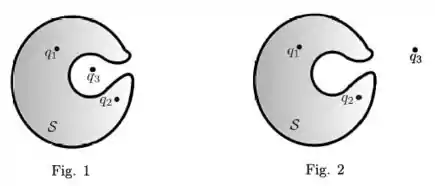
Sobre esse sistema, é correto afirmar que:
- O fluxo do campo elétrico gerado apenas por através de tem o mesmo valor nas duas situações.
- Em ambas as situações, o campo elétrico em toda a superfície se deve apenas à superposição dos campos gerados por e .
- O fluxo do campo elétrico total através da superfície vale na Fig. 1 e na Fig. 2.
- As linhas de campo elétrico na Fig. 1 são indistinguíveis das linhas de campo elétrico na Fig. 2.
- Em ambas as situações, o campo elétrico gerado apenas pela carga é nulo em todos os pontos da superfície .
Questão 21
A figura abaixo mostra as linhas do campo eletrostático produzido por um par de partículas de cargas e . A figura mostra ainda duas superfícies imaginárias e fechadas, e , indicadas pelas linhas tracejadas. A superfície envolve apenas a partícula de carga , enquanto envolve as duas partículas. Considere que o vetor normal a estas superfícies aponta para fora delas, seguindo a orientação usual. Sobre essa situação, considere as afirmativas abaixo:
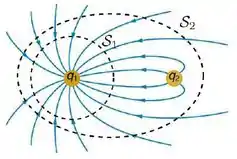
(I) O fluxo de campo eletrostático através de vale .
(II) O fluxo de campo eletrostático através de é negativo.
(III) O fluxo de campo eletrostático através de é nulo.
São VERDADEIRAS as afirmativas:
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) Apenas I e II
(e) Apenas I e III
(f) Apenas II e III
(g) I, II e III
(h) Nenhuma delas
Ver solução completaQuestão 22
Uma partícula de carga q é posicionada sobre a origem de um sistema de coordenadas. Considere a superfície fechada mostrada na figura abaixo, formada pela interseção de uma superfície esférica de raio e centro na origem com os planos , e . Nessa situação, o fluxo de campo elétrico produzido pela partícula através de vale:
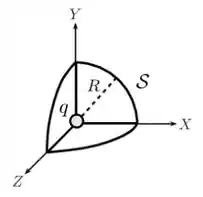
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 23
10 - A figura abaixo mostra as linhas do campo eletrostático produzidas por um par de partículas de cargas q1 e q2. A figura mostra ainda duas superfícies imaginárias e fechadas, S1 e S2, indicadas pelas linhas tracejadas. A superfície S1 envolve apenas a partícula de carga q1, enquanto S2 envolve as duas partículas. Sobre essa situação, considere as afirmativas abaixo:
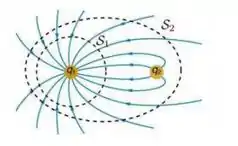
- O fluxo de campo eletrostático através de S1 vale .
- O fluxo de campo eletrostático através de S1 é negativo.
- O fluxo de campo eletrostático através de S2 é nulo.
São VERDADEIRAS as afirmativas:
- Apenas I
- Apenas II
- Apenas II
- Nenhuma delas
- I, II e III
Questão 24
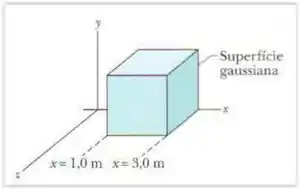
(Cap 23 Ex- 3) O cubo da Fig. 23-27 tem 1,40 m de aresta e está orientado da forma mostrada na figura em uma região onde existe um campo elétrico uniforme. Determine o fluxo elétrico através da face direita do cubo, se o campo elétrico, em Newtons por coulomb, é dado por (a) (d) Qual é o fluxo total através do cubo nos três casos?
Ver solução completaQuestão 25
(Cap 23 Ex- 2) Um campo elétrico dado por E = 4,0î – 3,0(y2 + 2,0)ĵ atravessa um cubo gaussiano com 2,0 m de aresta, posicionado da forma mostrada na Fig. 23-5. (E é dado em Newtons por coulomb e x em metro .) Determine o fluxo elétrico (a) através da face superior; (b) através da face inferior; (c) através da face da esquerda; (d) através da face traseira. (e) Qual é o fluxo elétrico total através do cubo?
Ver solução completaQuestão 26
Considere um plano infinito, uniformemente carregado, coincidente com o plano de um dado sistema de coordenadas. Sobre o campo elétrico produzido por este plano, considere as afirmativas abaixo:
(I) é independente das coordenadas e .
(II) A direção de é paralela ao eixo em todos os pontos do espaço.
(III) aponta no mesmo sentido em todos os pontos do espaço.
São VERDADEIRAS as afirmativas:
(a) Apenas I e II
(b) Apenas I
(c) Apenas II
(d) Apenas III
(e) Apenas I e III
(f) Apenas II e III
(g) I, II e III
(h) Nenhuma delas
Ver solução completaQuestão 27
Considere um disco circular isolante, fino, de raio , carregado com uma carga total uniformemente distribuída sobre sua superfície. Desenha-se então uma superfície imaginária S, fechada, na forma de um cilindro circular reto de raio , comprimento e eixo coincidente com o eixo do disco. Suas tampas são paralelas ao disco e equidistantes dele. Sobre essa situação, considere as afirmativas abaixo:
(I) O fluxo de campo elétrico produzido pelo disco através de é igual a .
(II) O campo elétrico produzido pelo disco é perpendicular à superfície lateral do cilindro em todos os pontos da mesma.
(III) O campo elétrico produzido pelo disco tem a mesma intensidade em todos os pontos sobre as tampas do cilindro.
São VERDADEIRAS as afirmativas:
Escolha uma:
a. Apenas II
b. I, II e III
c. Nenhuma delas
d. Apenas I e II
e. Apenas II e III
f. Apenas I
g. Apenas III
h. Apenas I e III
Ver solução completaQuestão 28
Esse enunciado utiliza os dados de matrícula dos alunos, mas nós do RA adaptamos para você!
Para calcular o campo elétrico de três distribuições de carga distintas, um aluno utiliza as superfícies gaussianas (em azul) contidas nas Figuras 1 a 3.
Para todas as geometrias acima, considere que a carga está uniformemente distribuída (todas as distribuições possuem densidade volumétrica de carga constante). Calculando o fluxo do campo elétrico que atravessa cada superfície gaussiana em função da distância o aluno montou os seguintes gráficos: 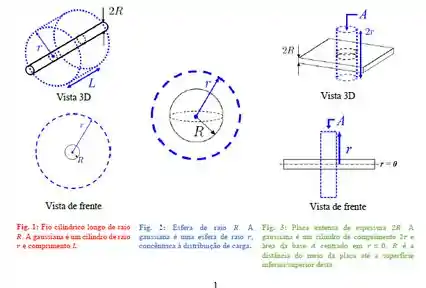
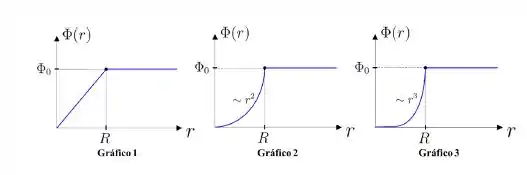
Com base nestas informações:
a) Associe cada gráfico a sua respectiva geometria de carga (cilíndrica, esférica, planar).
Sendo e .
b) Calcule o módulo do campo elétrico na superfície da distribuição de carga.
c) Qual o valor de ?
d) (1.0) Qual seria a nova forma do fluxo se ao invés de uma densidade de carga constante tivéssemos a densidade variável dada por:
Ver solução completaQuestão 29
Considere três objetos carregados:
- um fio retilíneo, posicionado entre os pontos e , com densidade linear de carga ( é uma constante);
- uma chapa plana, ocupando o quadrado , com densidade superficial ( é constante), e
- um sólido, ocupando o cubo ,, com densidade volumar ( é constante).
Todos esses objetos encontram-se no interior de uma superfície fechada . Qual das alternativas abaixo corresponde ao fluxo elétrico através da superfície ?
Escolha uma:
- O fluxo é nulo.
Questão 30
A figura abaixo mostra os planos infinitos e feitos de material não condutor, eletrificados com densidades superficiais de carga e , respectivamente.
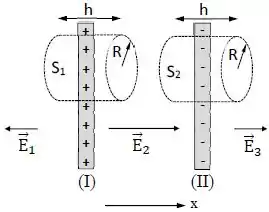
O campo elétrico à esquerda é , no centro é e à direita é . Além disso, estão indicadas duas superfícies gaussianas cilíndricas, e , de altura e raio , cujos eixos são perpendiculares aos planos de carga.
Sejam o fluxo através da superfície , e a densidade superficial de carga no plano .
Os valores de e são dados por:
, , , .
, , , .
, , , .
, , , .
, , , .
Ver solução completaQuestão 31
Suponha que exista uma superfície gaussiana fechada, cujo fluxo do campo elétrico é zero, para que isso seja verdade podemos dizer que:
- Existe a possibilidade de o campo elétrico ser nulo;
- Existe a possibilidade de não existir cargas em seu interior;
- Existe a possibilidade de em seu interior haver cargas elétricas, com a condição de serem dipolos elétricos
- Somente a afirmativa 3 está correta
- Somente as afirmativas 1 e 2 estão corretas
- Todas as afirmativas estão corretas
- Somente a afirmativa 1 está correta
- Somente a afirmativa 2 está correta
Questão 32
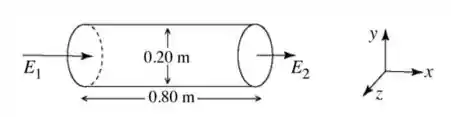
Considere uma região do espaço preenchida por um campo elétrico não uniforme dado por . O eixo de uma superfície cilíndrica, com de comprimento e de diâmetro, está alinhado paralelamente ao eixo , conforme mostrado na figura. Os campos elétricos e , nas extremidades da superfície cilíndrica, têm magnitudes de e , respectivamente, e são direcionados como mostrado na figura. Qual é, aproximadamente, o fluxo de campo elétrico resultante que passa pela superfície cilíndrica?
A)
B)
C)
D)
E)
Ver solução completaQuestão 33
. Uma esfera isolante de raio está carregada de forma que seu hemisfério superior possui uma densidade volumétrica de carga constante e positiva enquanto seu hemisfério inferior possui uma densidade volumétrica de carga constante e negativa . Considere uma superfície imaginária e fechada na forma de um hemisfério de raio , como mostra a figura abaixo. Esta superfície é composta por uma superfície hemisférica aberta , que define o hemisfério, e pela base plana , que divide as regiões de carga positiva e negativa da esfera.
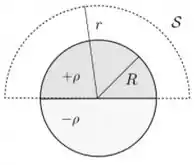
Sobre essa situação, considere as afirmativas abaixo:
O campo elétrico produzido pela esfera tem módulo constante em todos os pontos da superfície hemisférica aberta .
O campo elétrico produzido pela esfera é perpendicular a todos os pontos da base plana .
O fluxo do campo elétrico produzido pela esfera através de vale .
É (são) VERDADEIRA(S) a(s) afirmativa(s):
Escolha uma opção:
Nenhuma delas
e
e
e
e
Ver solução completaQuestão 34
Uma bola esférica de cobre tem raio e se encontra em posição concêntrica dentro de uma cavidade esférica de cobre de raio intermo . Na esfera interna existe uma elétrica .
(b) Calcule o trabalho necessário para transportar uma carga da parede da cavidade até a bola interna.
Ver solução completaQuestão 35
Usando a lei de Gauss, calcule o fluxo do campo elétrico através de uma das faces de um cubo que tem de lado e está carregado com uma densidade volumétrica de carga .
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 36
Uma esfera isolante de raio está uniformemente carregada com uma carga total . Desenhamos então uma superfície quadrada , de lado , que corta a esfera ao meio, como mostrado na figura abaixo.
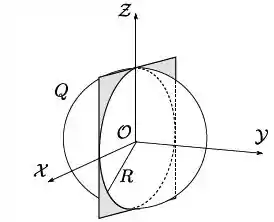
Essa superfície é desenhada de forma a coincidir com o plano de um sistema de coordenadas com origem no centro da esfera, e a sua normal é escolhida ao longo de positivo.
Dessa forma, qual é o fluxo de campo elétrico através de ?
Ver solução completaQuestão 37
Considere a superfície tracejada orientada quadrada , com versor (vetor unitário) normal e os seis campos elétricos constantes , , que só tem componentes e .
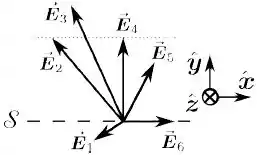
Indique a alternativa que melhor ordena os fluxos através da superfície (não esqueça dos sinais).
.
.
Sem saber a área do quadrado, é impossível realizar a ordenação.
.
.
Ver solução completaQuestão 38
Um capacitor de placas paralelas é conectado a uma bateria até que fique completamente carregado. A bateria é desligada e as placas do capacitor são deslocadas de modo que a separação entre as placas seja a metade da separação original. Seja a nova diferença de potencial entre as placas e a diferença de potencial do capacitor quando estava ligado à Bateria. A relação é:
Questão 39
Questão 40
Uma partícula de carga está localizada no centro de uma superfície esférica gaussiana de área e o volume de sua região interior é . Em qual das situações abaixo o fluxo do campo elétrico através da superfície gaussiana em questão será alterado?
Escolha uma:
a. A partícula é deslocada do centro para outro ponto, ainda no interior da superfície original.
b. A superfície é transformada em uma superfície cúbica, de mesma área mas volume diferente de em seu interior, com a partícula mantida em seu interior.
c. A superfície é transformada em uma superfície cúbica, de área diferente de mas com o mesmo volume em seu interior, com a partícula mantida em seu interior.
d. Uma segunda partícula é colocada próxima à superfície original, mas do lado de fora.
e. A partícula é movida para fora da superfície original.
Ver solução completaQuestão 41
Considere a figura abaixo em que o sólido é um cubo de aresta 1. O campo elétrico é uniforme e tem direção e sentido do eixo com módulo .
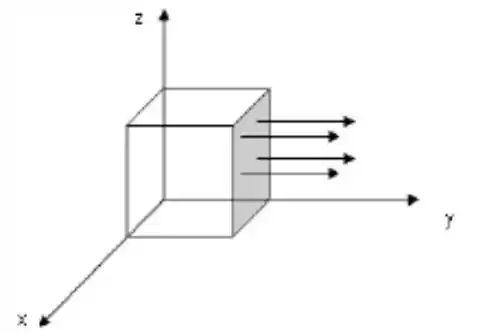
Determine o fluxo elétrico através do cubo, em unidades do SI.
Dado:
Ver solução completaQuestão 42
Um campo elétrico não-uniforme é direcionado ao longo do eixo em todos os pontos no espaço. A magnitude do campo varia com , mas não com respeito a ou . O eixo de uma superfície cilíndrica, com de comprimento e de diâmetro, é alinhado paralelamente ao eixo , como mostrado na figura abaixo. Os campos elétricos e , nas extremidades da superfície cilíndrica, têm magnitudes de e , respectivamente, e são dirigidos como mostrado. Quanto vale, aproximadamente, o fluxo elétrico que passa pela superfície cilíndrica?
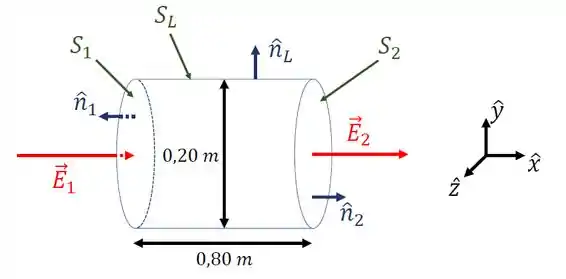
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 43
As cargas e encontram-se no interior da superfície gaussiana representada pelo hexágono da figura abaixo, enquanto a carga encontra-se no exterior da superfície gaussiana. Seja o fluxo de campo elétrico total através da superfície Gaussiana e , e representam os fluxos de campo elétrico gerados individualmente pelas cargas , e , respectivamente. A respeito dos fluxos de campo elétrico definidos, a alternativa CORRETA é:
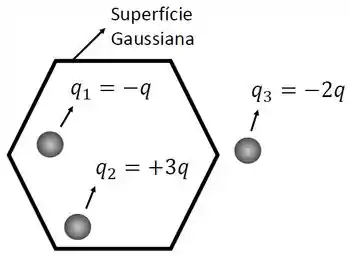
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 44
O fluxo de um campo elétrico uniforme orientado ao longo do eixo , através da superfície total de um cubo de lado é igual a:
Ver solução completaQuestão 45
Quando o fluxo do campo elétrico calculado sobre uma superfície esférica for nulo, podemos concluir que não há partículas carregadas no interior da esfera. Verdadeiro ou falso?
Ver solução completaQuestão 46
Sabendo que o fluxo do campo elétrico é o produto escalar do vetor campo elétrico com o vetor normal da superfície gaussiana, suponha que em determinada superfície gaussiana o vetor normal a superfície é e o vetor campo elétrico é . Determine o valor do fluxo do campo elétrico
Ver solução completaQuestão 47
Considere um condutor isolado e em equilíbrio com uma carga Q. Ao traçarmos uma superfície gaussiana em seu interior, verificamos que o campo elétrico é nulo. Isso é devido a:
- A carga distribui-se na superfície externa do condutor;
- O campo não depende do material do condutor, mas somente das cargas;
- O campo depende do material condutor e da carga envolvida
- Somente a afirmativa 2 está correta.
- Somente a afirmativa 3 está correta.
- Somente as afirmativas 1 e 2 estão corretas.
- Somente as afirmativas 1 e 3 estão corretas.
- Somente a afirmativa 1 está correta.