Forças Não Conservativas
Produzido por Ludovic BeghinTeoria
As forças não conservativas são qualquer tipo de força que atua em um sistema transformando energia mecânica em outras formas de energia. Um exemplo muito comum do nosso dia a dia é a força de atrito!
-Beleza, mas na prática, qual é a diferença entre forças conservativas e não conservativas?
No caso das forças conservativas como, por exemplo, a força gravitacional, a trajetória não influencia no trabalho realizado, apenas vai importar a posição inicial e a final.
Já para as forças não conservativas, a trajetória influencia no trabalho realizado!
Bora entender isso melhor?
Influência da Trajetória
Na figura abaixo você pode ver o skatista percorrendo duas pistas, ambas possuem o mesmo coeficiente de atrito e a mesma altura, em qual delas o trabalho da
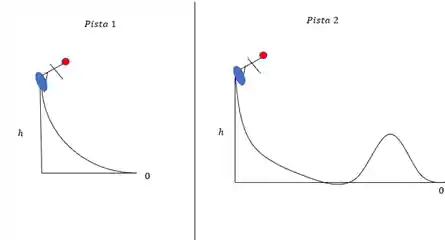
Repara o seguinte aqui, ambas as pistas começam na altura
Ambas as pistas possuem o mesmo coeficiente de atrito, mas o pulo do gato está na trajetória, você lembra como se calcula o trabalho de uma força?
Usamos a seguinte fórmula:
Onde
No nosso caso, a força de atrito está sempre contrária ao movimento, e por isso faz um ângulo de
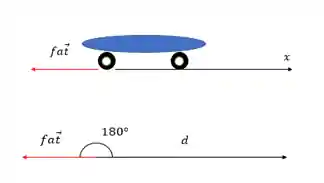
E como o
E o que significa esse sinal negativo no trabalho da força de atrito?
Basicamente, significa que o trabalho da
Agora vamos analisar o que acontece em cada pista, na pista
E na pista
Como:
A gente pode dizer que:
Ou seja, a distância percorrida influencia no trabalho da força de atrito e vai influenciar no trabalho de qualquer força não conservativa!
Variação da Energia Mecânica
-Será que as forças não conservativas vão sempre gerar um trabalho negativo e diminuir a energia do sistema?
-NÃO!
Imagina um esquiador descendo uma rampa, e ao longo dessa rampa, a força do vento está ajudando sua descida.
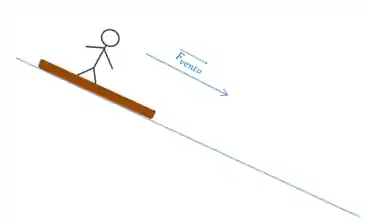
Nesse caso, como a força do vento
E nesse caso, o trabalho será positivo, o que indica que a energia do sistema irá aumentar, ou seja, esse esquiador vai chegar na base dessa rampa com uma velocidade maior do que no caso onde não haveria essa força do vento.
Como calcular a variação de energia?
O trabalho de uma força não conservativa vai ser a variação da energia mecânica do sistema:
Por isso que um trabalho positivo faz o sistema ganhar energia e um trabalho negativo faz o sistema perder energia.
Arrumando essa equação, nós temos:
Bora fazer um exemplo?
Exemplo: Um carrinho com massa
A resolução desse problema você pode conferir no vídeo abaixo! 👇
Bora praticar com exercícios?
Variação da Energia Mecânica
Como calcular a variação de energia?
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 218 – Modificado
O freio de um caminhão de massa deixa de funcionar quando ele está descendo uma estrada de montanha com gelo inclinada de um ângulo . Inicialmente o caminhão desce a montanha com velocidade . Depois de percorrer, com atrito desprezível, uma distância até a base da montanha, o motorista vira o voltante e faz o caminhão seguir por uma estrada de emergência para caminhões. A estrada para caminhões é pavimentada com areia fofa que possui um atrito de rolamento igual a . Qual é à distância percorrida pelo caminhão desde a rampa até parar? Use o método da energia.
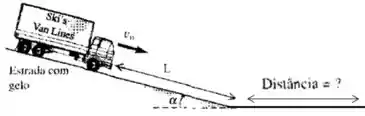
Passo 1
Vamos seguir a recomendação do enunciado e usar o método da energia.
Antes, vamos escrever os dados do problema
Ele quer a distância percorrida (vamos chamá-la de ), mas lembre-se ela não é dada.
A única força não conservativa q temos é a
Como o corpo está parado, e está no chão
Temos então
Devemos encontrar cada energia e o trabalho da força de atrito
Passo 2
Vamos achar as energias primeiro,
Passo 3
Repare que não temos a altura do caminhão, porém temos
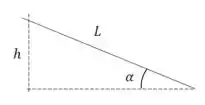
Então, vamos “decompor”
Então
Passo 4
Vamos agora achar o trabalho da , para isso devemos achar primeiro o seu módulo
Para encontrarmos , vamos usar sua fórmula
Nessa região a normal será igual ao peso (não estamos mais no plano inclinado)
Passo 5
Para encontrarmos seu trabalho
Isso porque a força está no sentido contrário ao deslocamento.
Então
Passo 6
Recapitulando
Queremos resolver
Tendo
Substituindo teremos
Beleza, então achamos a distância , que é quanto o caminhou andou na parte reta. Mas, notem que a questão pede a distância total que o camihão andou desde a rampa até parar. Então, a distância total, , vai ser a distância da rampa, , mais a parte reta, .
Resposta
Exercício Resolvido #2
PUCRIO-Física I-Prova 2-2013.2-Questão 2
Dois blocos idênticos de massa ligados por um fio ideal estão dispostos como mostra na figura abaixo. O bloco , se encontra sobre uma superfície horizontal cujo coeficiente de atrito cinético vale enquanto o bloco encontra-se pendurado. O sistema parte do repouso e ambos os blocos tem a mesma velocidade até o momento em que o bloco toca a mola. A constante elástica da mola é desconhecida. Determine:
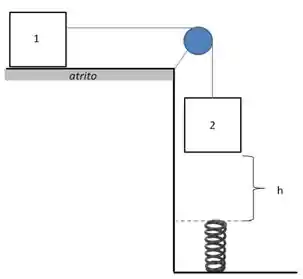
o trabalho realizado pela força de atrito no sistema quando o bloco cai uma altura . Este trabalho é positivo ou negativo? Justifique.
A velocidade do bloco ao tocar a mola.
Quando o bloco toca a mola, o fio entre os blocos é cortado instantaneamente. Observa-se que a velocidade do bloco neste instante é de . Sabendo que a compressão máxima que será produzida na mola é . Determine:
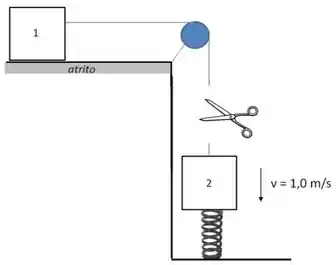
a constante elástica da mola em .
a que distância abaixo do ponto inicial de contato entre o bloco e a mola encontra-se o ponto de equilíbrio do sistema bloco e mola.
Passo 1
Para determinar o trabalho realizado pela força de atrito, devemos lembrar da definição de trabalho:
Pelo fato de existir um vínculo entre os blocos, se o bloco , cai uma altura de , isso significa que o bloco também se deslocou . Voltando à equação do trabalho, lembrando que a força de atrito cinético, nesse caso, é dada por , temos:
Substituindo os valores conhecidos, temos:
Pelo fato de a força de atrito se opor ao movimento, temos que o trabalho realizado é negativo, portanto:
Passo 2
Para determinar a velocidade do bloco ao tocar na mola, devemos utilizar o seguinte teorema que relaciona o trabalho das forças não conservativas com a variação da energia mecânica, pois existe uma força de atrito, que não é conservativa, atuando.
Já calculamos o trabalho realizado por essa força, ele vale . A variação da energia mecânica, pode ser determinada da seguinte forma:
Pensando em nosso sistema, que é composto pelos dois blocos, temos a seguinte variação da energia mecânica:
Lembrando que somente o bloco está variando de altura, ou seja, somente ele possui , além do fato de que por estarem ligados por um fio, os blocos possuem a mesma velocidade. Por partirem do repouso, a velocidade inicial é zero!
Substituindo os valores conhecidos, temos:
Passo 3
Para determinar a constante elástica da mola, vamos utilizar a conservação da energia mecânica, entre o momento antes de o bloco tocar na mola, e o momento em que a deformação é máxima:
Perceba que o meu potencial zero está na altura da deformação máxima da mola, que é . Substituindo os valores, temos:
Passo 4
Na situação de equilíbrio do sistema bloco mola, temos que satisfazer a seguinte relação:
Onde o peso do bloco deve ser igual à força elástica, temos então:
Substituindo os valores, temos:
Resposta
, negativo, pois a força de atrito se opõem ao movimento.
Exercício Resolvido #3
UFRJ-Física 1-Prova 1-2013.1 Múltipla Escolha n°2
Um pequeno bloco de massa sobre uma mesa horizontal comprime uma mola de constante elástica de uma distância , a partir da posição relaxada da mola em , como mostra a figura. Liberado a partir do repouso, ele realiza um movimento retilíneo horizontal para a direita, onde ele perde o contato com a mola depois da posição , percorrendo em seguida uma distância , quando atinge o repouso; há uma força de atrito constante da supercifie da mesa sobre o bloco em toda a extensão do movimento. O coeficiente de atrito cinético entre a superfície e o bloco é:
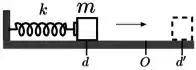
Passo 1
Vamos começar escrevendo os dados do problema
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
No enunciado ele pede o coeficiente de atrito cinético, que é o coeficiente quando ele está se movendo. Nesse problema temos uma força dissipativa atuando, que é a força de atrito. Então
Onde é a energia mecânica em e é a energia mecânica em .
Precisamos achar , é e .
Começando por
O sinal do trabalho é negativo porque a força de atrito é no sentido contrário do movimento.
Já vimos em muitos outros exercícios que, no caso do bloco no plano
Então
Vamos agora achar as energias mecânicas. Em ambos os pontos não temos velocidade nem mudança de altura. A única energia é a potencial elástica, que está presente apenas no inicio.
Como ele perde contato com a mola no ponto ele não tem energia elástica
Lembrando rapidinho
Resposta
Letra
Exercício Resolvido #4
UFRJ-Física 1-Prova 1-2014.1 Questão n°2
A figura mostra o perfil suave de uma calha com um trecho inclinado , seguido de um trecho horizontal , que é seguido de um outro trecho inclinado ; as alturas do ponto e do ponto acima do solo são iguais a e o comprimento do trecho horizontal é igual a . Um bloco de massa e dimensões desprezíveis desce a partir do ponto , onde o módulo da sua velocidade é e percorre os trechos , e . O coeficiente de atrito cinético entre o bloco e a calha no trecho é , e entre o bloco e a calha nos trechos e é zero. Considerando como dados , , e o módulo da aceleração da gravidade, calcule:
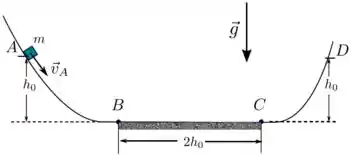
- Os trabalhos das forças peso e normal nos trechos , e ;
- O trabalho da força de atrito no trecho ;
- A variação da energia cinética do ponto ao ponto e o módulo da velocidade do bloco em ;
Passo 1
Vamos começar escrevendo os dados da questão
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
Já vimos que com ao normal é sempre perpendicular a superfície o trabalho dela será zero.
Passo 3
Para calcularmos o trabalho da força peso, devemos nos preocupar apenas com o deslocamento vertical, então
Ele será positivo porque o peso está no sentido do deslocamento vertical
Nesse trecho não temos deslocamento vertical
Ele será negativo porque o peso está no sentido contrário do deslocamento vertical
Passo 4
b)
O trabalho da é negativo porque ele é contra o movimento.
Já vimos em muitos outros exercícios que, no caso do bloco no plano
Então
Passo 5
c)
Pelo teorema trabalho-energia cinética
Onde
Então
Passo 6
Para achar a velocidade vamos achar a variação de energia cinética pela fórmula da energia cinética